|
WIKI Funktionsanalyse - Globales Verhalten
|


1. Globalverhalten von Funktionen
| Mithilfe des Globalverlaufs bzw. Globalverhaltens untersuchen wir das Verhalten der Funktionswerte (y-Werte) einer Funktion, wenn die Definitionswerte (x-Werte) positiv oder negativ unendlich groß werden (x→∞ und x→-∞), sofern der Definitionsbereich für diese Bereiche überhaupt definiert ist. |
| Das Globalverhalten wird auch Verhalten an den Grenzen des Systems, auch „Verhalten im Unendlichen“ genannt. |
| Bei ganzrationalen Funktionen z. B. gibt es vier unterschiedliche Globalverläufe. Zwischen den beiden "Enden" der Funktion können beliebig viele Maxima, Minima und Wendepunkte liegen. Betrachten wir uns das Globalverhalten einzelner Funktionsklassen einmal genauer. |
2. Globalverhalten der einzelnen Funktionsklassen
2.1. Konstante Funktionen der Form f(x)=C
| Eine konstante Funktion der Art f(x)=C ist eine Parallele zur x-Achse im Abstand C. Wie wir aus der Grafik erkennen, hat eine solche Funktion im gesamten Definitionsbereich einen konstanten Wert. Wir können also nicht von einem Globalverhalten reden. | 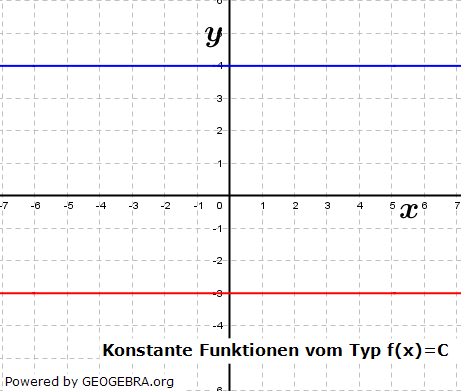 |
2.2. Ganzrationale Funktionen
| Ganzrationale Funktionen haben die Form: | 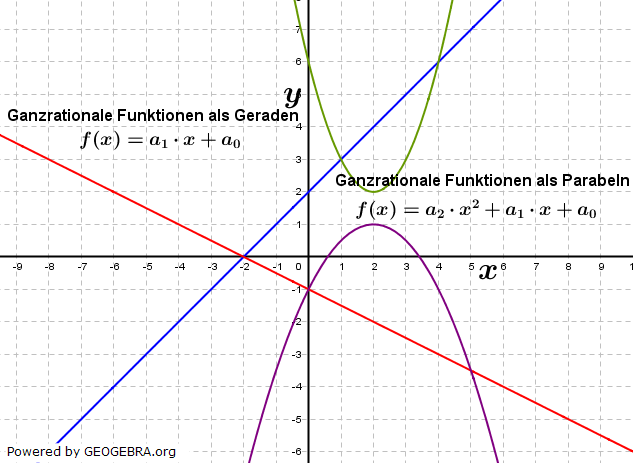 |
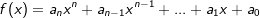 |
|
| Je nach Ausprägung des Maximalwertes von n sprechen wir von ganzrationalen Funktionen n-ten Grades bzw. n-ter Ordnung. Bestimmte Grade haben zusätzliche Namen. | |
| Bei n=1 sprechen wir von linearen Funktionen, bei n=2 sprechen wir von Parabeln. Für Werte n>2 finden wir auch Bezeichnungen wie Parabel n-ter Ordnung oder auch Polynomen. | |
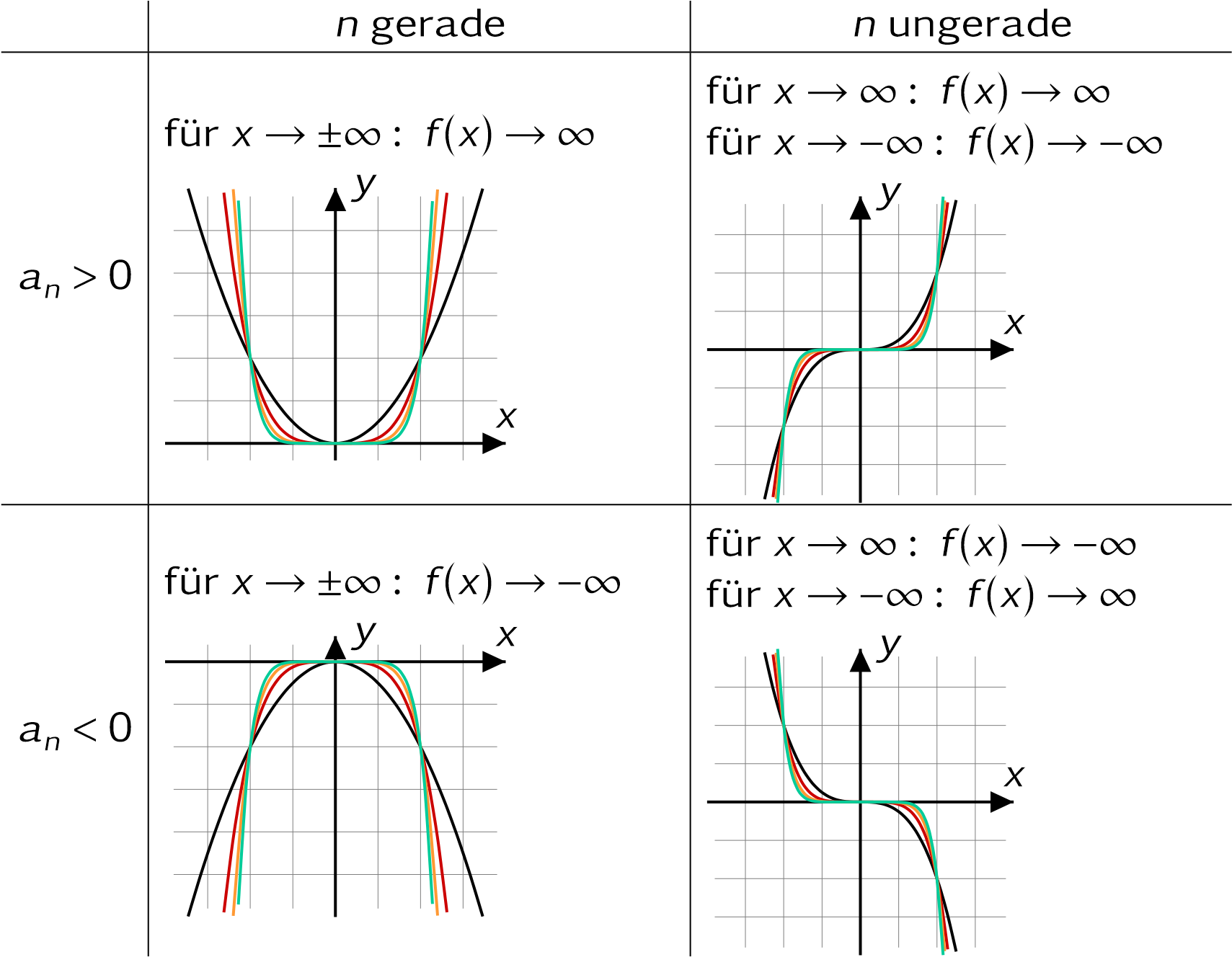
Alle ganzrationalen Funktionen haben als Definitionsbereich 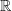 , d.h., sie sind definiert für alle Werte von x und zwar von -∞ bis +∞. Damit besitzen diese Funktionen auch ein globales Verhalten. , d.h., sie sind definiert für alle Werte von x und zwar von -∞ bis +∞. Damit besitzen diese Funktionen auch ein globales Verhalten.Das Verhalten dieser Funktionen wird ausschließlich bestimmt von der höchsten Potenz von x (also ihrem Grad) und dem zugehörigen Koeffizienten. In der nachfolgenden Abbildung ist das Verhalten im Unendlichen für verschiedene Exponenten in Abhängigkeit ihres zugeordneten Koeffizienten dargestellt. |
|
 |
|
| Für f mit f(x)=2x3-4x+2 Funktion ist vom Grad n=3 ⇒ n ist ungerade. Koeffizient a3=2 ⇒ a3>0 Über die Grafik lesen wir ab: Für x→-∞ verläuft f(x)→ -∞; für x→∞ verläuft f(x)→ ∞. Für g mit g(x)=-3x8+x2-1 Funktion ist vom Grad n=8 ⇒ n ist gerade. Koeffizient a8=-3 ⇒ a8<0 Über die Grafik lesen wir ab: Für x→-∞ verläuft f(x)→ -∞; für x→∞ verläuft f(x)→- ∞. |
| Diese Lösung setzt voraus, dass wir die Grafik generell vor Augen haben. Da dies jedoch nicht immer der Fall ist, oder wir uns die Grafik einfach nicht einprägen können, gibt es eine viel einfachere Methode, das globale Verhalten zu bestimmen, nämlich das „Minuszählen“. Beim „Minuszählen“ gilt: |
Merksatz Globales Verhalten durch Minuszählen
| Setze in die höchste Potenz von x -∞ ein und zähle die Anzahl der Minuszeichen einschließlich des Vorzeichens des Koeffizienten. | ||
| Ist die Anzahl der Minuszeichen ungerade, so verläuft f(x)→-∞ . Ist die Anzahl der Minuszeichen gerade, so verläuft f(x)→+∞. |
||
Setze in die höchste Potenz von x +∞ ein und stelle die Anzahl der Minuszeichen einschließlich des Vorzeichens des Koeffizienten fest. |
||
| Bei ungerader Anzahl der Minuszeichen verläuft f(x)→-∞ . Bei gerader Anzahl von Minuszeichen verläuft f(x)→+∞. |
2.2.2. Beispiel 2
| Bestimme das Globalverhalten von: f mit f(x)=-3x5+4x2-2 und g mit g(x)=0,5x6-x2-1 durch „Minuszählen“. |
| Für f mit f(x)=-3x5+4x2-2 mit der höchsten Potenz incl. Koeffizient -3x5. Wir setzen -∞ ein und erhalten -3⋅(-∞)⋅(-∞)⋅(-∞)⋅(-∞)⋅(-∞). Wir zählen 6 Minuszeichen ⇒ Anzahl Minuszeichen gerade: f(x)→+∞ Wir setzen ∞ ein und erhalten -3⋅(∞)⋅(∞)⋅(∞)⋅(∞)⋅(∞). Wir zählen 1 Minuszeichen ⇒ Anzahl Minuszeichen ungerade: f(x)→-∞ |
| Für g mit g(x)=0,5x6-x2-1 mit der höchsten Potenz incl. Koeffizient 0,5x6. Wir setzen -∞ ein und erhalten 0,5⋅(-∞)⋅(-∞)⋅(-∞)⋅(-∞)⋅(-∞)⋅(-∞). Wir zählen 6 Minuszeichen ⇒ Anzahl Minuszeichen gerade: f(x)→+∞ Wir setzen ∞ ein und erhalten 0,5⋅(∞)⋅(∞)⋅(∞)⋅(∞)⋅(∞)⋅(∞). Wir zählen 0 Minuszeichen ⇒ Anzahl Minuszeichen gerade: f(x)→∞ |
2.3. Gebrochen rationale Funktionen
| Gebrochen rationale Funktionen haben die Form: | 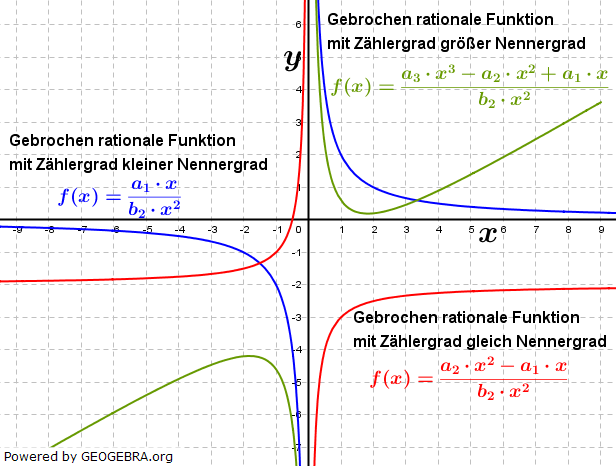 |
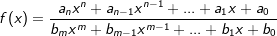 |
|
| Bei gebrochen rationalen Funktionen müssen wir zunächst nach höchster Potenz im Zähler und höchster Potenz im Nenner unterscheiden. Generell können wir feststellen, dass nur gebrochen rationale Funktionen ein | |
| Globalverhalten aufweisen können, bei denen der Zählergrad größer ist als der Nennergrad. Alle anderen gebrochen-rationale Funktionen weisen im Unendlichen asymptotisches Verhalten auf (siehe auch Asymptoten in diesem Kapitel). | |
| Wie wir in der Abbildung sehen, verlaufen der blaue Graph und der rote Graph für x→±∞ gegen einen festen Wert, der blaue Graph verläuft gegen Null, der rote Graph gegen -2. Das ist zwar auch ein Verhalten im Unendlichen, allerdings sprechen wir hier nicht mehr von globalem Verhalten sondern von Asymptoten. Der grüne Graph hingegen verläuft für x→±∞ wie eine Gerade ins Unendliche. | |
| Auch hier gilt für das globale Verhalten die Aussage wie bei den ganzrationalen Funktionen, dass nur die höchste Potenz von x zu berücksichtigen ist. Allerdings müssen wir diese höchste Potenz zunächst mal durch eine Division von höchster Potenz im Zähler und höchster Potenz im Nenner bilden: |
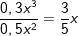 Und mit diesem Ausdruck verfahren wir jetzt wie bei den ganzrationalen Funktionen. |
Wir setzen -∞ ein und erhalten 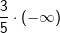 . .Wir zählen 1 Minuszeichen ⇒ Anzahl Minuszeichen gerade: f(x)→-∞ Wir setzen ∞ ein und erhalten 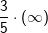 . .Wir zählen 0 Minuszeichen ⇒ Anzahl Minuszeichen gerade: f(x)→∞ |
2.4. Trigonometrische Funktionen
| Trigonometrische Funktionen haben die Form: | 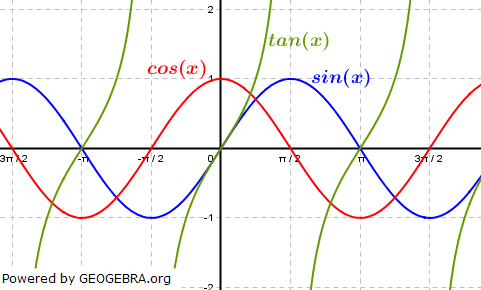 |
| f(x)=a⋅sin(b(x-c))+d bzw. f(x)=a⋅cos(b(x-c))+d bzw. f(x)=a⋅tan(b(x-c))+d. Da trigonometrische Funktionen solche mit periodisch wiederkehrenden |
|
| Funktionswerten sind, zeigen diese kein globales Verhalten. | |
2.5. Exponential-Funktionen
| Exponential-Funktionen haben die Form: f(x)=a⋅bx bzw. f(x)=a⋅ekx |
| Exponentialfunktionen zeigen globales Verhalten nur auf einer Seite des Graphen der Funktion. Dies ist abhängig vom Vorzeichen des Exponenten. Wir betrachten zunächst das Verhalten des Funktionsteils bx bzw. eax. |
Für x<0 können wir den Ausdruck b-x ja auch umschreiben zu 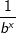 . . Für x→-∞ gilt ja nun 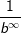 , also die Division von 1 mit einer riesengroßen Zahl. Dieser Wert läuft aber gegen Null, zeigt also asymptotisches und kein globales Verhalten. , also die Division von 1 mit einer riesengroßen Zahl. Dieser Wert läuft aber gegen Null, zeigt also asymptotisches und kein globales Verhalten. |
| Ist x hingegen > 0, so erhalten wir für x→∞ den Ausdruck b∞, ein riesengroßer Wert also. Somit handelt es sich um ein globales Verhalten, für x→∞ läuft bx→∞. Gleiches gilt natürlich für ekx. Die nachfolgernde Tabelle gibt Aufschluss darüber, für welche Werte von a und x die Exponentialfunktion asymptotisches bzw. globales Verhalten aufweist. |
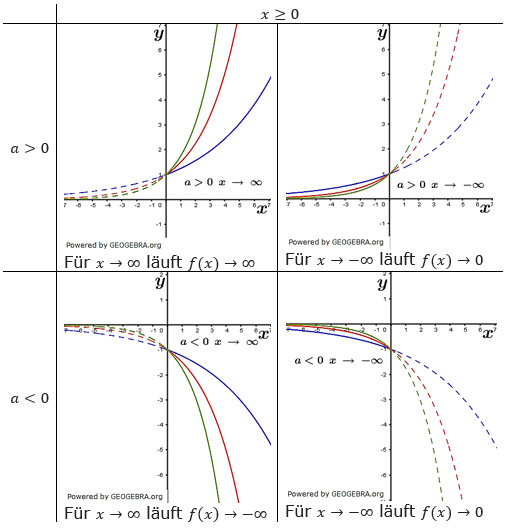 |
| Ist x≥0, so zeigt die Exponentialfunktion nur für x→∞ globales Verhalten. |
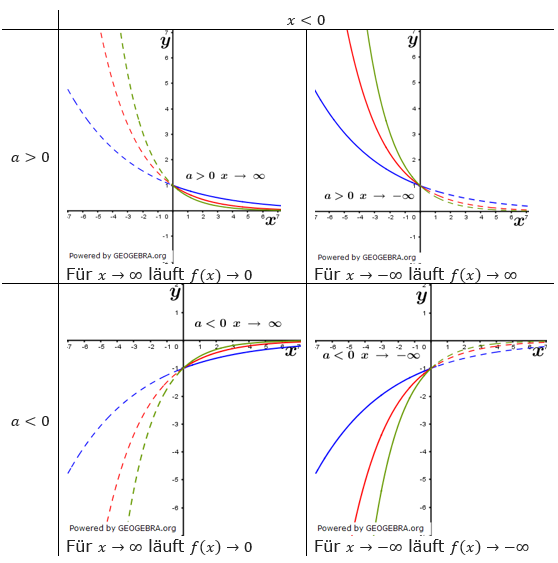 |
| Ist x<0, so zeigt die Exponentialfunktion nur für x→-∞ globales Verhalten. |
2.6. Logarithmus-Funktionen
| Logarithmus-Funktionen haben die Form: f(x)=a⋅logb(|x|) bzw. f(x)=a⋅ln(|x|) |
|
| Logarithmusfunktionen zeigen globales Verhalten nur auf einer Seite des Graphen der Funktion. Dies ist abhängig vom Vorzeichen des Koeffizienten a. Wir betrachten zunächst das Verhalten des Funktionsteils logb(|x|) bzw. ln(|x|). Da ein Logarithmus nur für Argumente größer x definiert ist, muss die Variable in Betragszeichen im Logarithmus stehen. Somit können wir das untersuchen wir das Globalverhalten für x→∞ und für x→-∞ untersuchen. | |
| Die nachfolgernde Tabelle gibt Aufschluss darüber, für welche Werte von a und x die Logarithmusfunktion globales Verhalten aufweist. | |
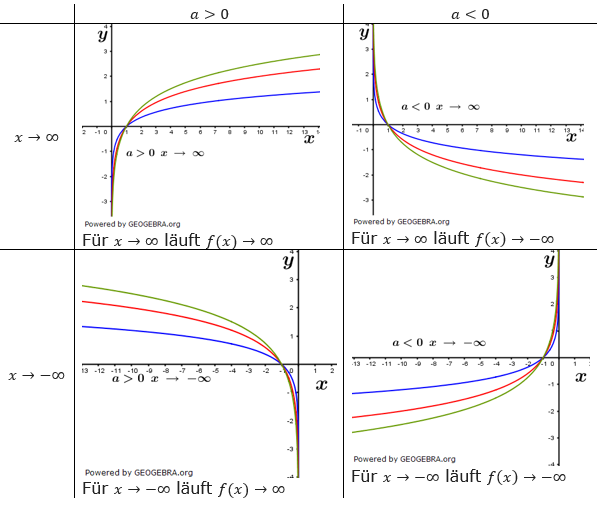 |
|
| Für a>0 gilt: | |
| f(|x|)→∞ wenn x>0 ∧ x→∞ bzw. wenn x< 0 ∧ x→-∞ | |
| Für a<0 gilt: | |
| f(|x|)→-∞ wenn x>0 ∧ x→∞ bzw. wenn x< 0 ∧ x→-∞ | |
| Du befindest dich hier: |
| WIKI Funktionsanalyse - Globales Verhalten |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 08. Juli 2021 08. Juli 2021

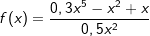 .
.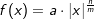 mit
mit