 |
Zinsrechnung (unterjährig) kennenlernen, üben und verstehen |
Regeln und Formeln
| Die Zinsrechnung ist eigentlich eine Prozentrechnung mit einer Einschränkung und einer Erweiterung. Die Einschränkung ist die, dass die Zinsrechnung sich ausschließlich mit Kapital befasst, während bei der Prozentrechnung ja alle möglichen Größen wie etwa Gewichtsmaße, Längenmaße, Flächen und Volumen, Geschwindigkeiten und vieles andere mehr in die Rechnung eingehen können, natürlich auch Kapital. Und damit kommen wir schon zur Erweiterung. Die Zinsrechnung berücksichtigt noch einen Zeitraum. Bei der Prozentrechnung spielt ein Zeitraum keine Rolle. Ob du nun ausrechnest, wie viel Prozent ein Auto schneller fährt als das Andere oder wie viel Gehalt mehr ein Arbeiter bei einer Lohnerhöhung von 4,2 % erhält oder um wie viel billiger ein Artikel im Sommerschlussverkauf ist bei 25 % Preissenkung, da spielt ein Zeitraum keine Rolle. Von der Zinsrechnung weißt du jedoch, dass beispielsweise eine Bank dein Sparguthaben mit 2,5 % verzinst. Diese 2,5 % verstehen sich jedoch als Prozentsatz für das Geld, was dir die Bank gutschreibt, wenn du dein Geld genau 1 Jahr bei der Bank hast. Lässt du das Geld nur 6 Monate auf der Bank, so erhältst du auch nur die Hälfte der Jahreszinsen gutgeschrieben. |
|
| Betrachten wir uns jetzt noch einmal das Prozentrechnungsschema und stellen diesem das Zinsrechnungsschema gegenüber. | |
  |
|
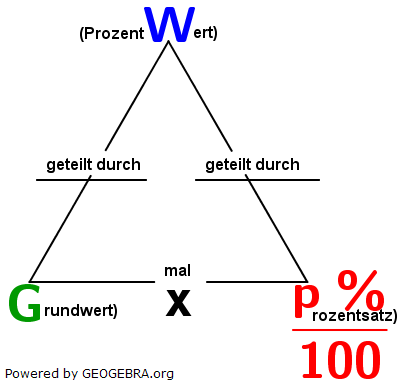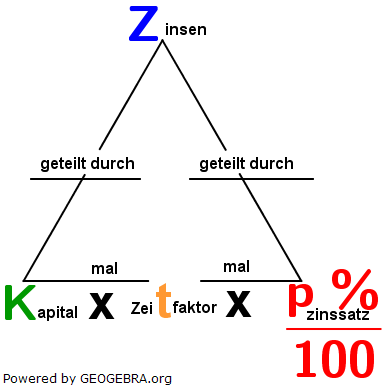| Wie du erkennen kannst, entsprechen in der Zinsrechnung die Zinsen dem Prozentwert der Prozentrechnung, das Kapital dem Grundwert und der prozentsatz dem pzinssatz. Im Zinsschema findest du jetzt noch einen weiteren Parameter mit t angegeben. Dieser Wert ist also die Erweiterung der Zinsrechnung gegenüber der Prozentrechnung. Das t ist das Abkürzungszeichen für die Zeit und kommt aus dem Lateinischen Wort tempus. Im Schema hat dieses t die Einheit Jahre. Wir bezeichnen es ab sofort mit dem Wort „Zeitfaktor“. |
|
Auswirkung und Bestimmung von t
| Wie groß ist denn nun dieses t? Nun, dieses t ist ja der Zeitfaktor, beschreibt also den Zeitraum, in dem ein bestimmter Geldbetrag angelegt bzw. ausgeliehen wird. Wenn dieser Zeitraum genau 1 Jahr ist, dann ist t=1 und damit können wir das t einfach weglassen. In diesem Falle ist die Zinsrechnung identisch mit der Prozentrechnung. | |||
| Dies führt uns zum ersten Merksatz der Zinsrechnung: Merksatz zum Zeitfaktor der Zinsrechnung
|
|||
 Und nun wollen wir sehen, was mit dem Zeitfaktor t ist, wenn dieser nicht gleich 1 ist, also Zinswerte für einen Zeitraum zu berechnen sind, der nicht genau 1 Jahr lang ist. |
|||
| Zunächst noch etwas zur Begriffserklärung von t. Die Formeln der Zinsrechnung gelten nur für Zeiträume zwischen einem und 360 Tagen. In der Zinsrechnung hat jeder Monat 30 Tage, unabhängig davon, ob der Kalendermonat 28, 29, 30 oder 31 Tage hat. Somit hat ein ganzes Jahr 12∙30 Tage = 360 Tage. Da aber 360 Tage gleich ein Jahr sind, wird bei 360 Tagen t=1. Bei mehr als 360 Tagen darfst du die im Folgenden erläuterten Berechnungen nicht mehr anwenden, denn das ist dann Sache der Zinseszinsrechnung . |
|||
| Nun hat das t in den Berechnungen aber immer die Einheit Jahr. Sollst du nun aber Aufgaben lösen, die Monate oder gar Tage als Zeitraum haben, so musst du zunächst diesen angegebenen Zeitraum in Jahr umrechnen. So sind ja z.B. 6 Monate = 0,5 Jahre, 3 Monate = 0,25 Jahre usw. Es geht aber auch einfacher. Wenn du x Monate hast, wobei das x nur zwischen 1 und 12 liegen darf, so schreibst du für t einfach: | |||
 |
|||
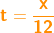| Wenn du jetzt aber Tage als Zeitraum angegeben hast, so kannst du diese leicht in Monate umrechnen, wenn die Anzahl der gegebenen Tage durch 30 geteilt werden kann. So sind 30 Tage gleich einem Monat, 240 Tage = 8 Monaten usw. Es geht aber auch einfacher. Wenn du x Tage hast, wobei das x nur zwischen 1 und 360 liegen darf, so schreibst du für t einfach: | |||
 |
|||
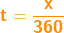| In der Schule hast du vielleicht gelernt, dass man statt t „m“ schreiben soll, wenn es sich um Monate handelt und dass t für Tage steht. Das darfst du ganz schnell wieder vergessen. Es gibt in der Zinsrechnung nur einen einzigen Parameter für den Zeitraum und der lautet t mit der Einheit Jahr. Monate und Tage müssen in Jahr umgerechnet werden. |
Beispiel 1
| Ermittle die Anzahl Tage zur Zinsermittlung, wenn ein Sparguthaben vom 6.6. bis zum 20.11. bei der Bank angelegt ist. |
 |
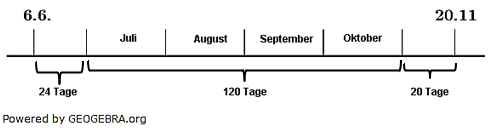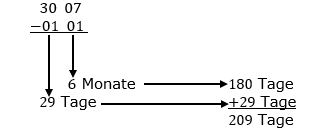
| Also 24 Tage vom 6.6. bis Ende Juni, dann 4∙30 Tage für Juli, August, September und Oktober und 20 Tage im November. 24 Tage + 120 Tage + 20 Tage =164 Tage |
| Hinweis Bei Einzahlungen zählt der Tag der Einzahlung nicht zu den Zinstagen, wohl aber der Tag der Abhebung des Kapitals. Im Beispiel erkennt man das am Einzahlungstag 6.6. Vom 6.6. bis 30.6. sind es einschließlich des 6.6. insgesamt 25 Tage. Die gebildete Differenz ergibt aber 30-6=24 |
.Zinsrechnung kennenlernen und üben
| Betrachten wir uns noch einmal das Zinsschema. Gegenüber der Prozentrechnung hast du ja jetzt vier Parameter an Stelle von drei. Also müssen dir für die Berechnungen stets 3 Werte gegeben sein, damit du den gesuchten Wert ausrechnen kannst. Somit gibt es aber auch vier mögliche Arten von Berechnungen, nämlich: Gegeben: Kapital, Zinssatz und Zeitfaktor Gesucht: Zinsen Gegeben: Zinsen, Zinssatz und Zeitfaktor Gesucht: Kapital Gegeben: Kapital, Zinsen und Zeitfaktor Gesucht: Zinssatz Gegeben: Kapital, Zinsen und Zinssatz Gesucht: Zeitfaktor Zum Kennenlernen und Üben dieser vier Berechnungsmöglichkeiten • Zinsen • Kapitel • Zinssatz • Zeitfaktor klicke einfach auf das gewünschte Thema im seitlichen Menü. |
| Du befindest dich hier: |
| Zinsrechnung (unterjährig) kennenlernen, üben und verstehen |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 14. Juli 2021 14. Juli 2021
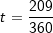