Unter dem unbestimmten Integral verstehen wir die Menge aller Stammfunktionen F(x), die sich aus einer gegebenen Funktion f(x) durch Integration ergeben.
Vom Prinzip ist diese Definition nichts anderes als die Definition der Integralrechnung als Umkehrrechenart der Differentialrechnung. Wir schreiben hierfür: |
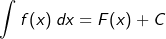 |
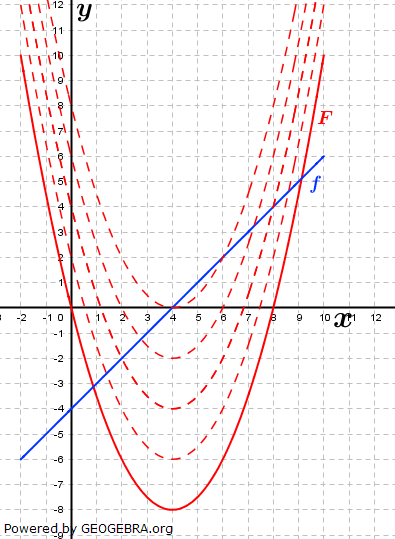
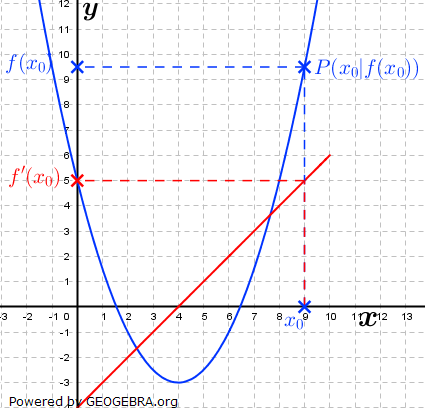 Es gilt nun, zu verstehen, was das Zeichen dx und die Variable C bedeuten. Hierzu gehen wir zum besseren Verständnis einmal den umgekehrten Weg und haben zum Beispiel einer quadratische Funktion mit Es gilt nun, zu verstehen, was das Zeichen dx und die Variable C bedeuten. Hierzu gehen wir zum besseren Verständnis einmal den umgekehrten Weg und haben zum Beispiel einer quadratische Funktion mit 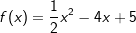 und bilden deren Ableitung f'(x)=2x-4. Nebenstehende Grafik zeigt den Verlauf der Graphen von f und f'. und bilden deren Ableitung f'(x)=2x-4. Nebenstehende Grafik zeigt den Verlauf der Graphen von f und f'.
Aus dem Gebiet Differenzialrechnung heraus wissen wir, dass f'(x) die Steigung von f(x) an jeder beliebigen Stelle x0 liefert. Diese Steigung ist aber nichts anderes als die momentane Änderungsrate im Punkt P(x0│f(x0 )), was gleichzeitig die Steigung der Tangente an f in diesem Punkt mit der Gleichung |
| t(x)=f'(x0)∙(x-x0 )+f(x0) ist. |
Die momentane Änderungsrate einer Kurve bzw. die Steigung ist aber definiert über den Differenzialquotienten 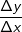 auch mit auch mit 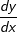 bezeichnet. Somit ist der Ausdruck f'(x) nichts anderes als eine Abkürzung für bezeichnet. Somit ist der Ausdruck f'(x) nichts anderes als eine Abkürzung für 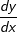 . Somit können wir auch schreiben: . Somit können wir auch schreiben: |
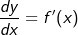 |
| Diese Gleichung wandeln wir nach den Regeln der Äquivalenzumformung um: |
|
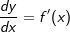 |
|
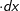 |
|
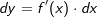 |
|
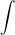 |
|
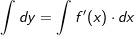 |
|
|
| und da die Integralrechnung die Umkehrrechenart der Differentialrechnung ist, erhalten wir wieder |
|
 |
|
|
| also f(x), was uns ja die y–Koordinate einer Funktion an jeder beliebigen Stelle x0 liefert. |
Zur Erklärung der Variablen C sehen wir uns nun die Ermittlung einer Ursprungsgleichung aus einer gegebenen Ableitungsgleichung heraus an.
Wir bleiben bei obigem Beispiel. Gegeben ist die Ableitungsfunktion f mit f(x)=x-4 einer Stammfunktion F. Zu bestimmen ist die Ursprungsgleichung. Wir wenden die Umkehrregel zur Differentialrechnung an und schreiben: |
 |
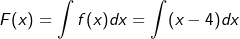 |
Wir wissen, dass das x aus 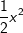 und die -4 aus -4x entstanden ist. Das führt uns zur Funktionsgleichung und die -4 aus -4x entstanden ist. Das führt uns zur Funktionsgleichung 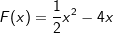 . Doch, wo ist denn die 5 aus unserem obigen Beispiel geblieben? . Doch, wo ist denn die 5 aus unserem obigen Beispiel geblieben? |
Da durch eine Ableitung die Information über das absolute Glied der Stammfunktion verloren geht, denn die Ableitung einer Konstanten 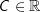 ist gleich 0, erhalten wir durch Integration einer Funktion f keinerlei Information mehr über den ursprünglichen Wert des absoluten Gliedes der Stammfunktion. Aus diesem Grund müssen wir jeder durch Integration ermittelten Stammfunktion die Variable +C hinzufügen. Die Stammfunktion ist somit keine einzelne Funktion mehr, sondern vielmehr eine unendliche Menge von Stammfunktionen, die wegen ist gleich 0, erhalten wir durch Integration einer Funktion f keinerlei Information mehr über den ursprünglichen Wert des absoluten Gliedes der Stammfunktion. Aus diesem Grund müssen wir jeder durch Integration ermittelten Stammfunktion die Variable +C hinzufügen. Die Stammfunktion ist somit keine einzelne Funktion mehr, sondern vielmehr eine unendliche Menge von Stammfunktionen, die wegen 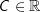 alle in y–Richtung nach oben oder unten verschoben sind. alle in y–Richtung nach oben oder unten verschoben sind. |




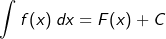
 Es gilt nun, zu verstehen, was das Zeichen dx und die Variable C bedeuten. Hierzu gehen wir zum besseren Verständnis einmal den umgekehrten Weg und haben zum Beispiel einer quadratische Funktion mit
Es gilt nun, zu verstehen, was das Zeichen dx und die Variable C bedeuten. Hierzu gehen wir zum besseren Verständnis einmal den umgekehrten Weg und haben zum Beispiel einer quadratische Funktion mit 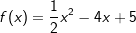 und bilden deren Ableitung f'(x)=2x-4. Nebenstehende Grafik zeigt den Verlauf der Graphen von f und f'.
und bilden deren Ableitung f'(x)=2x-4. Nebenstehende Grafik zeigt den Verlauf der Graphen von f und f'.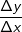 auch mit
auch mit 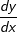 bezeichnet. Somit ist der Ausdruck f'(x) nichts anderes als eine Abkürzung für
bezeichnet. Somit ist der Ausdruck f'(x) nichts anderes als eine Abkürzung für 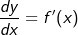
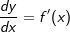
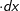
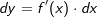
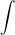
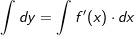
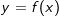

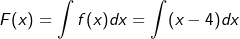
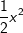 und die -4 aus -4x entstanden ist. Das führt uns zur Funktionsgleichung
und die -4 aus -4x entstanden ist. Das führt uns zur Funktionsgleichung 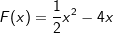 . Doch, wo ist denn die 5 aus unserem obigen Beispiel geblieben?
. Doch, wo ist denn die 5 aus unserem obigen Beispiel geblieben?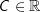 ist gleich 0, erhalten wir durch Integration einer Funktion f keinerlei Information mehr über den ursprünglichen Wert des absoluten Gliedes der Stammfunktion. Aus diesem Grund müssen wir jeder durch Integration ermittelten Stammfunktion die Variable +C hinzufügen. Die Stammfunktion ist somit keine einzelne Funktion mehr, sondern vielmehr eine unendliche Menge von Stammfunktionen, die wegen
ist gleich 0, erhalten wir durch Integration einer Funktion f keinerlei Information mehr über den ursprünglichen Wert des absoluten Gliedes der Stammfunktion. Aus diesem Grund müssen wir jeder durch Integration ermittelten Stammfunktion die Variable +C hinzufügen. Die Stammfunktion ist somit keine einzelne Funktion mehr, sondern vielmehr eine unendliche Menge von Stammfunktionen, die wegen 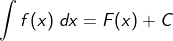
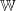 einer Stammfunktion können nicht mehr getroffen werden, sind also unentscheidbar.
einer Stammfunktion können nicht mehr getroffen werden, sind also unentscheidbar.

