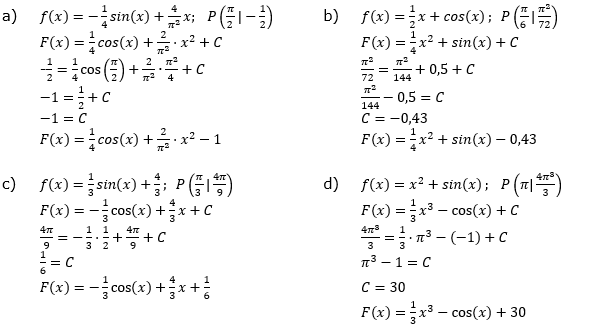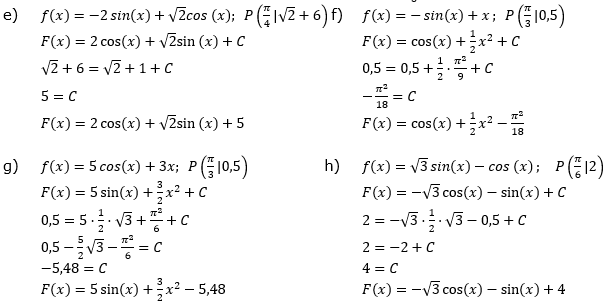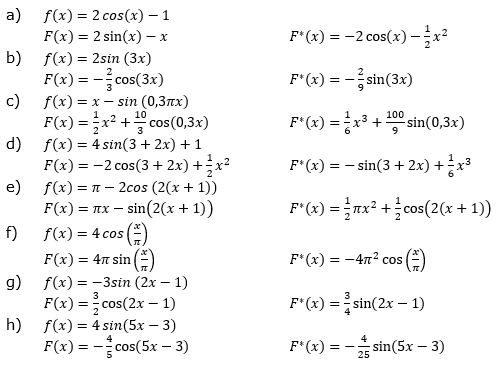 |
Stammfunktionen Trigonometrie - Level 2 - Fortgeschritten - Blatt 4 |
| Dokument mit 21 Aufgaben |
Aufgabe A1 (8 Teilaufgaben)
| Bestimme die Stammfunktion F von f, deren Graph durch den Punkt P(xp |yp) verläuft. | |
| a) |  |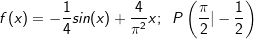
| b) |  |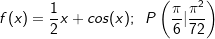
| c) |  |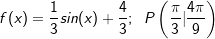
| d) |  |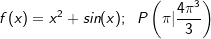
| e) |  |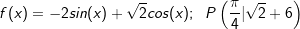
| f) |  |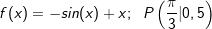
| g) |  |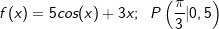
| h) |  |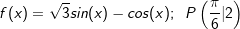
 Eine Frage stellen... |
Fehler melden...
Aufgabe A2 (3 Teilaufgaben)
| F sei eine Stammfunktion von f mit f(x)=sin(x) im Intervall [0;2π]. F verläuft durch den Punkt P(0|-2). In welchen Punkten hat F dieselbe Steigung wie | |
| a) | die erste Winkelhalbierende; |
| b) | die x-Achse; |
| c) | die Gerade mit der Gleichung  ? |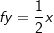
| Eine Frage stellen... |
Aufgabe A3 (2 Teilaufgaben)
| Gegeben ist die Funktion f mit f(x)=2cos(x) für x ∈ [0;2π]. Eine Stammfunktion F von f geht durch den Punkt P(0|-2). | |
| a) | An welchen Stellen x0 gilt F(x0 )=-1? |
| b) | Gibt es Stellen mit F(x0 )>1? |
| Eine Frage stellen... |
Aufgabe A4 (8 Teilaufgaben)
| Bilde jeweils eine Stammfunktion F von f sowie eine weitere Stammfunktion F* von F. | |
| a) | f(x)=2cos(x)-1 |
| b) | f(x)=2sin(3x) |
| c) |  |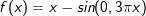
| d) | f(x)=4 sin(3+2x)+1 |
| e) |  |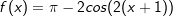
| f) |  |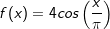
| g) | f(x)=-3sin(2x-1) |
| h) | f(x)=4sin(5x-3) |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Stammfunktionen Trigonometrie Level 2 - Fortgeschritten - Blatt 4 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 25. Januar 2022 25. Januar 2022
