 |
WIKI unbestimmtes Integral - Integrationsregeln komplex |

1. Unbestimmtes Integral / Integrationsregeln komplex
| Nachfolgend sind die gegenüber den Basisregeln der Integration erweiterten Integrationsregeln im einzelnen aufgeführt. Die hier aufgeführten Regeln entsprechen dem Lehrumfang in den ersten Semestern von Analysis-Vorlesungen an Universitäten bzw. ähnlich gelagerten Bildungseinrichtungen wie z. B., technischen Hochschulen. Die Integrationsregeln der Basis findest du im Kapitel "Integrationsregeln Basis". |
2. Nicht lineare Substitution
| Ist im Integranden eines Integrals eine verkettete Funktion und außerdem noch die Ableitungsfunktion der inneren Funktion als Faktor vorhanden, so kann die Integration durch nichtlineare Substitution erfolgen. |
Merksatz nicht lineare Substitution
| Es sei f(x)=v(u(x))⋅u'(x) und V eine Stammfunktion der äußeren Funktion v, dann ist F mit F(x)=V(u(x)) eine Stammfunktion von f. | |||
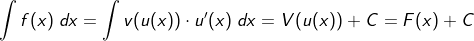 |
|||
Einsetz
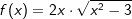 |
|||
Wir erkennen zunächst in der Funktionsgleichung, dass u(x)=x2-3 ist. Somit ist 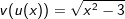 und u'(x)=2x. und u'(x)=2x.Die gegebene Funktionsgleichung ist somit Kandidat für nichtlineare Substitution. |
|||
| z=u(x)=x2-3 | | | Substitution | |
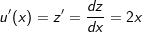 |
| | 1. Ableitung von z | |
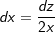 |
| | Umstellung nach dx | |
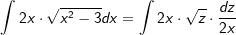 |
| | Einsetzen z und dx in das Integral | |
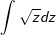 |
| | 2x kürzt sich heraus | |
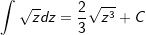 |
| | Bildung Stammfunktion Z | |
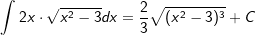 |
| | Resubstitution von z=x2-3 | |
| Die Stammfunktion lautet somit: | |||
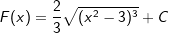 |
|||
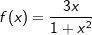 |
|||
| Zunächst erkennen wir nicht, dass in der Funktionsgleichung sowohl u(x) als auch u'(x) vorkommt. Zwar könnten wir u(x)=1+x2 setzen, dann wäre u'(x)=2x. Im Zähler des Bruchs steht aber 3x. | |||
| Die Überlegung ist nun, ob es uns gelingt, durch eine geeignete Rechenoperation die benötigten 2x im Zähler zu erzeugen. Die nachfolgende Umformung zeigt einen geeigneten Weg: |
|||
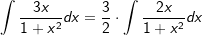 |
|||
| Durch die Umformung steht nun im Zähler die Ableitung des Nenners, die gegebene Funktionsgleichung ist somit Kandidat für nichtlineare Substitution. | |||
| z=u(x)=1+x2 | | | Substitution | |
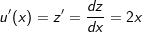 |
| | 1. Ableitung von z | |
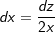 |
| | Umstellung nach dx | |
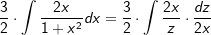 |
| | Einsetzen z und dx in das Integral | |
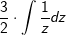 |
| | 2x kürzt sich heraus | |
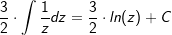 |
| | Bildung Stammfunktion Z | |
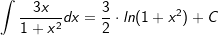 |
| | Resubstitution von z=1+x2 | |
| Die Stammfunktion lautet somit: | |||
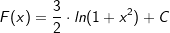 |
|||
3. Partielle Integration
| Bereitet die Integration einer Summe von Funktionen wenig Probleme unter Verwendung der Summen- bzw. Differenzregel, gestaltet sich das Integrieren eines Produktes von Funktionen weitaus schwieriger. |
| Bislang haben wir für solche Fälle die Integration durch lineare Substitution bzw. nicht lineare Substitution kennen gelernt, doch kann man in vielen Fällen keine geeignete Substitution angeben. |
| Jedoch ermöglicht eine einfache Umkehrung der Produktregel der Ableitungen von Funktionen den Zugang zum Integrationsverfahren der partiellen Integration. |
| Für die Ableitung eines Produktes von Funktionen f(x)=u(x)⋅v(x) gilt: f'(x)=u'(x)⋅v(x)+u(x)⋅v'(x). Wir integriert auf beiden Seiten, so folgt nach der Summenregel der Integralrechnung |
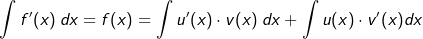 |
| Mit f(x)=u(x)⋅v(x) erhalten wir: |
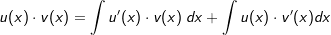 |
Jetzt bringen wir 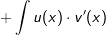 mit "-" auf die andere Seite der Gleichung und haben somit: mit "-" auf die andere Seite der Gleichung und haben somit: |
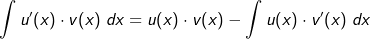 |
| Somit lässt sich der folgende Merksatz formulieren: |
Merksatz partielle Integration
| Sind u und v im Intervall [a;b] differenzierbare Funktionen sowie u' und v' im Intervall stetig, so gilt: | |||
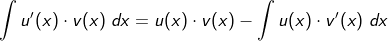 |
|||
| Die auf dieser Regel fußende Integrationsmethode nennen wir „partielle Integration“, um anzudeuten, dass ein Restintegral bleibt, d.h., wir integrieren nur teilweise – nur partiell. Dieses Restintegral ist entweder ein bekanntes Grundintegral oder es muss weiter evtl. abermals partiell integriert werden. |
|||
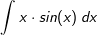 |
| Für diesen Integranden finden wir keine geeignete Substitution. Wenden wir die partielle Integration an, müssen wir entscheiden, welchen der beiden Faktoren im Integranden wir für u und welchen wir für v' einsetzen. |
| Hierzu bedarf es einiger Sorgfalt, denn wählt man u und v' falsch herum, wird das Integral komplizierter statt einfacher. Wir wählen u(x)=x und v'(x)=sin(x). Dann wird u'(x)=1 und v(x)=-cos(x) |
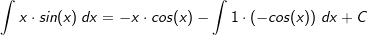 |
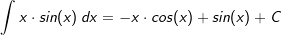 |
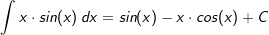 |
| Die Stammfunktion lautet somit: F(x)=sin(x)-x⋅cos(x)+C |
Wählen wir aber u(x)=sin(x) und v'(x)=x, dann wird u'(x)=cos(x) und 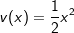 . . |
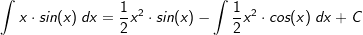 |
| Das hierbei entstandene Restintegral ist komplizierter als das bei der ersten Ersetzung. |
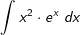 |
|
| Dieses Beispiel haben wir bereits in den Basis-Integrationsregeln unter Formansatz mit Koeffizientenvergleich behandelt. In diesem WIKI lösen wir das Integral mittels partieller Integration. | |
| Wir wählen u(x)=x2 und v'(x)=ex. Dann wird u'(x)=2x und v(x)=ex |
|
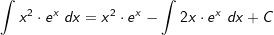 |
|
Für das Restintegral 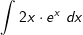 benötigen wir eine erneute partielle Integration. benötigen wir eine erneute partielle Integration. |
|
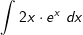 |
|
| Wir wählen u(x)=2x und v'(x)=ex. Dann wird u'(x)=2 und v(x)=ex |
|
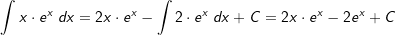 |
|
| Wir setzen die Lösung des Restintegrals in den ersten Teil ein: | |
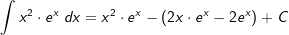 |
|
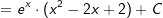 |
|
| Die Stammfunktion lautet somit: F(x)=ex⋅(x2-2x+2)+C |
|
4. Partialbruchzerlegung
| Die Partialbruchzerlegung bei der Integration wird auf gebrochen rationale Funktionen angewandt, sofern der Funktionsterm nicht durch eine einfache Division in eine Summe umgewandelt werden kann. |
| Ist der Integrand eine unecht gebrochen rationale Funktion – der höchste Zählergrad ist größer als der höchste Nennergrad -, so wird diese zunächst durch Polynomdivision in eine ganzrationale Funktion und eine echt gebrochen rationale Funktion zerlegt. |
| Den echt gebrochen rationalen Anteil schreibt man dann mittels Partialbruchzerlegung als eine Summe einfacher Teilbrüche. |
| Der Lösungsansatz für die Partialbruchzerlegung ist hierbei davon abhängig, ob die Funktion im Nenner einfache oder mehrfache, reelle oder komplexe Nullstellen hat. In diesem WIKI betrachten wir nur Fälle, in der die Funktion des Nenners einfache oder mehrfache reelle Nullstellen besitzt. |
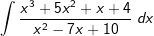 |
||
| Der Integrand ist hier eine unecht gebrochenrationale Funktion. In einem solchen Fall ist die Funktion vor der Partialbruchzerlegung in eine ganzrationale Funktion und eine echt gebrochenrationale Funktion zu zerlegen. Dies geschieht durch Polynomdivision. | ||
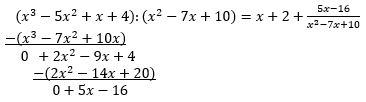 |
||
| Damit folgt für den angegebenen Quotienten: | ||
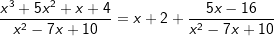 |
||
| Auf den echt gebrochenern Anteil der Funktion wenden wir nun die Partialbruchzerlegung an. Zunächst ermitteln wir die Nullstellen des Nenners: | ||
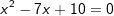 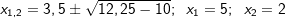 |
||
| Damit kann der Restbruch auch geschrieben werden mit: | ||
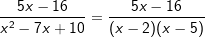 |
||
| Der Nenner mit (x-2)(x-5) ist offensichtlich der gemeinsame Nenner der Addition / Subtraktion zweier Brüche. Wir könnten also sagen, dass | ||
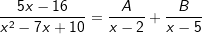 ist. ist. |
||
| Bilden wir wieder den gemeinsamen Nenner und erhalten (incl. Erweiterung): | ||
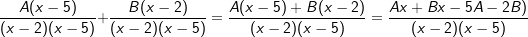 . . |
||
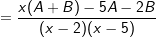 . . |
||
| Wir machen den Koeffizientenvergleich dieses Ergebnisses mit dem Original-Restbruch | ||
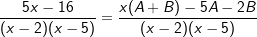 . . |
||
| Sodass daraus das Gleichungssystem folgt: | ||
| (I) | A+B=5 | |
| (II) | -5A-2B=-16 | |
| (I) | A=5-B | |
| A->(II) | ||
| (II) | -5(5-B)-2B=-16 | |
| -25+5B-2B=-16 | ||
| 3B=9 | ||
| B=3 | ||
| B->(I) | ||
| (I) | A+3=5 | |
| A=2 | ||
Somit ist der Bruch zerlegt und wir haben 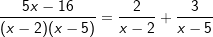 . . |
||
| Nun können wir die Ausgangsfunktion integrieren, denn | ||
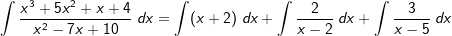 |
||
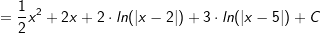 . . |
||
Die Stammfunktion lautet somit: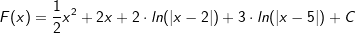 |
||
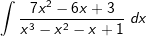 |
||
| Da es sich um einen echten Bruch handelt, entfällt die Polynomdivision. Wir bestimmen die Nullstellen des Nenners. Durch Ausprobieren ermitteln wir eine Nullstelle bei x1=1. Zur Reduzierung des Nennergrades führen wir eine Polynomdivsion durch: |
||
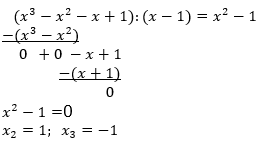 |
||
| Somit haben wir eine doppelte Nullstelle bei x1=1 und eine einfache bei x3=-1. Daraus folgt für die gegebene Funktionsgleichung |
||
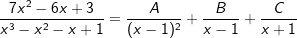 |
||
| Wir erweitern die Einzelbrüche auf ihren Hauptnenner: | ||
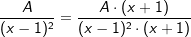 |
||
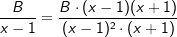 |
||
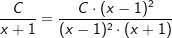 |
||
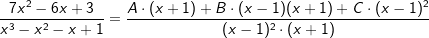 |
||
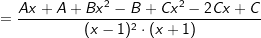 |
||
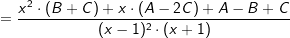 |
||
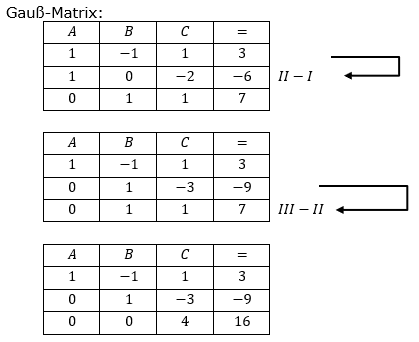
| Der Koeffizientenvergleich ergibt: | ||
| (I) | B+C=7 | |
| (II) | A-2C=6 | |
| (III) | A-B+C=3 | |
 |
||
| Aus (III) folgt: C=4 | ||
| C->(II) | ||
| (II) | B-3⋅4=-9 | |
| B=3 | ||
| B;C->(I) | ||
| (I) | A-3+4=3 | |
| A=2 | ||
| Dadurch erhalten wir: | ||
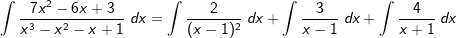 |
||
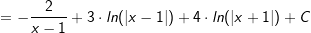 |
||
Die Stammfunktion lautet somit: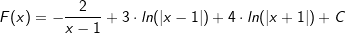 |
||
| Du befindest dich hier: |
| WIKI unbestimmtes Integral - Integrationsregeln komplex |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 25. Januar 2022 25. Januar 2022

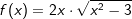 .
.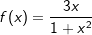 .
.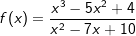 .
.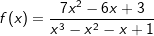 .
.

