|
|
Differenzialrechnung - Änderungsraten |


Änderungsraten Einleitung
| Wir können viele Bereiche unseres Lebens ja mit messbaren Größen beschreiben. So messen wir z. B. die Entfernung zwischen zwei Städten in Kilometer. Wir bestimmen den Inhalt einer Flasche in Litern, das Gewicht eines Körpers in Gramm oder Kilogramm, die Konzentration eines Medikaments in Milliliter, usw., usw. |
Wir bezeichnen diese unterschiedlichen Messgrößen mit dem Buchstaben G. Auf der anderen Seite kann es ja vorkommen, dass eine solche Messgröße nicht konstant ist, sondern im Verlaufe eines Zeitabschnittes sich verändert. Wenn wir mit dem Auto von Stuttgart nach Hamburg fahren, so ist die gesamte Wegstrecke ja etwa 650 km. Wir benötigen hierzu etwa 6,5 Stunden. Sind wir aber erst etwa zwei Stunden gefahren, so befinden wir uns erst im Raum Frankfurt am Main und haben somit erst 195 km Wegstrecke zurückgelegt. Auf der anderen Seite kann es ja vorkommen, dass eine solche Messgröße nicht konstant ist, sondern im Verlaufe eines Zeitabschnittes sich verändert. Wenn wir mit dem Auto von Stuttgart nach Hamburg fahren, so ist die gesamte Wegstrecke ja etwa 650 km. Wir benötigen hierzu etwa 6,5 Stunden. Sind wir aber erst etwa zwei Stunden gefahren, so befinden wir uns erst im Raum Frankfurt am Main und haben somit erst 195 km Wegstrecke zurückgelegt.Die zurückgelegte Wegstrecke auf unserer Fahrt ist also abhängig von der Zeit, die wir von Stuttgart aus gesehen, unterwegs sind. Wir bezeichnen diese Zeitdifferenz mit Δt, wobei Δt=t2 -t1 ist, mit t1 als Anfangszeit und t2 als aktuelle Zeit zum Messpunkt. Auf unser Beispiel angewandt: Δt wäre für die gesamte Strecke Stuttgart -> Hamburg damit Δt=6,5-0=6,5 Stunden und für die Strecke Stuttgart -> Frankfurt Δt=2-0=2 Stunden. Somit wäre für die Strecke Frankfurt -> Hamburg Δt=6,5-2=4,5 Stunden. |
Merksatz
| Die Änderungsrate einer zeitabhängigen Messgröße G beschreibt das Ausmaß der Veränderung von G in einem bestimmten Zeitraum im Verhältnis zur Dauer des Zeitraums Δt. Anschaulich gesprochen ist sie ein Maß dafür, wie schnell sich die Größe G ändert. Änderungsraten unterscheiden sich von Veränderungsangaben dadurch, dass sie immer ein Verhältnis der Form „Größe pro Zeit“ mit entsprechender Maßeinheit sind. Wir unterscheiden dabei zwischen mittlerer Änderungsrate und momentaner Änderungsrate. |
||
| Quelle: https://de.wikipedia.org/wiki/%C3%84nderungsrate | ||
Mittlere Änderungsrate
Merksatz
| Die mittlere Änderungsrate ist die durchschnittliche Änderung einer zeitabhängigen Messgröße G zwischen zwei Zeitpunkten t1 und t2, also im Zeitraum Δt=t2-t1. Berechnet wird sie als Quotient aus der Differenz der beiden Werte zu diesen Zeitpunkten ΔG=G(t2)-G(t1) und der Dauer Δt des Zeitraums ΔG/Δt. Im Zeit-Größen-Diagramm (Funktionsgraph, Schaubild) von G(t) ist die mittlere Änderungsrate zwischen t1 und t2 die Steigung der Sekante durch die Punkte (t1 |G(t1)) und (t2|G(t2)) auf dem Diagramm. | ||
| Quelle: https://de.wikipedia.org/wiki/Änderungsrate#Mittlere_.C3.84nderungsrate | ||
Momentane Änderungsrate
Merksatz
Die momentane Änderungsrate ist die auf einen „Moment“ (sehr kurzen Zeitraum) bezogene Veränderung einer zeitabhängigen Messgröße G. Sie kann mathematisch als Ergebnis des Grenzprozesses  als Ableitung G'(t) einer Zeit-G-Funktion G(t) dargestellt werden. als Ableitung G'(t) einer Zeit-G-Funktion G(t) dargestellt werden. |
||
| Quelle: https://de.wikipedia.org/wiki/%C3%84nderungsrate#Momentane_%C3%84nderungsrate | ||
| Nähere Einzelheiten und Regeln als auch Übungen findest du in den einzelnen Kapiteln „Mittlere Änderungsrate“ und „Momentane Änderungsrate“ hier im Portal. |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

 Einmal angenommen, wir hätten auf unserer Fahrt zwischen Stuttgart und Hamburg alle 10 Minuten die zurückgelegte Strecke über das Tachometer gemessen und die sich ergebenden Punkte in einem Koordinatensystem eingetragen und miteinander verbunden. Wir erhielten dann die in nebenstehender Grafik gestrichelt blau markierte Kurve.
Einmal angenommen, wir hätten auf unserer Fahrt zwischen Stuttgart und Hamburg alle 10 Minuten die zurückgelegte Strecke über das Tachometer gemessen und die sich ergebenden Punkte in einem Koordinatensystem eingetragen und miteinander verbunden. Wir erhielten dann die in nebenstehender Grafik gestrichelt blau markierte Kurve.
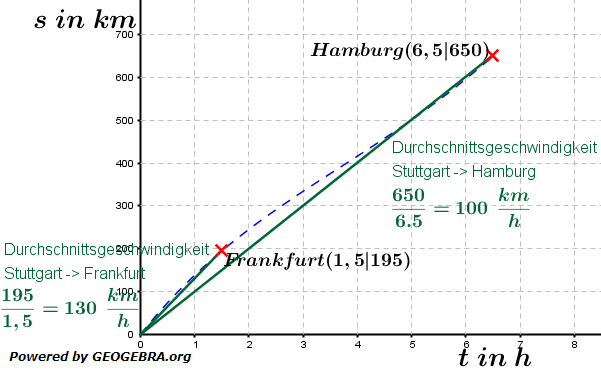
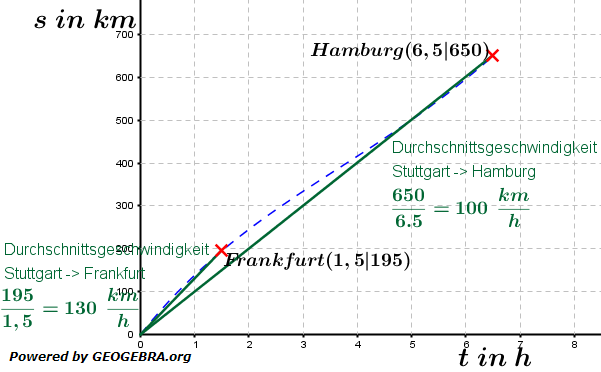
 . Vater Jan hat damit seine Durchschnittsgeschwindigkeit errechnet. Und diese Durchschnittsgeschwindigkeit ist nichts anderes, als die mittlere Änderungsrate im Zeitraum zwischen Abfahrtszeit (Stunde null) und Ankunftszeit Hamburg (Stunde 6,5).
. Vater Jan hat damit seine Durchschnittsgeschwindigkeit errechnet. Und diese Durchschnittsgeschwindigkeit ist nichts anderes, als die mittlere Änderungsrate im Zeitraum zwischen Abfahrtszeit (Stunde null) und Ankunftszeit Hamburg (Stunde 6,5). . Die mittlere Änderungsrate im Zeitraum zwischen Abfahrtszeit (Stunde null) und Ankunftszeit Frankfurt (Stunde 1,5) beträgt 130 km/h.
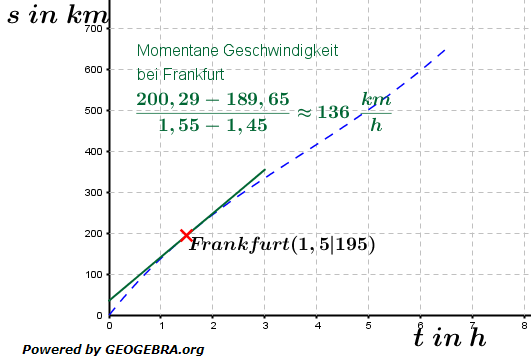
. Die mittlere Änderungsrate im Zeitraum zwischen Abfahrtszeit (Stunde null) und Ankunftszeit Frankfurt (Stunde 1,5) beträgt 130 km/h. Wie wir zuvor gesehen haben, gibt es auf der Strecke zwischen Stuttgart und Hamburg wohl unterschiedliche Geschwindigkeiten. Uns interessiert nun, welche Geschwindigkeit Vater Jan zu einem ganz bestimmten Zeitpunkt fährt. Hierzu betrachten wir den Punkt Frankfurt P(1,5|195).
Wie wir zuvor gesehen haben, gibt es auf der Strecke zwischen Stuttgart und Hamburg wohl unterschiedliche Geschwindigkeiten. Uns interessiert nun, welche Geschwindigkeit Vater Jan zu einem ganz bestimmten Zeitpunkt fährt. Hierzu betrachten wir den Punkt Frankfurt P(1,5|195).