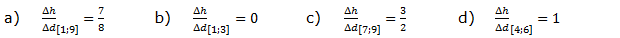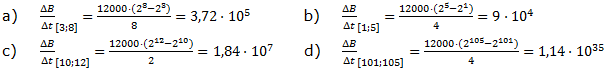 |
Mittlere Änderungsrate - Level 2 - Fortgeschritten - Blatt 1 |
| Dokument mit 10 Aufgaben |
Aufgabe A1
Während eines Dauerregens wird die Wassermenge V (in Liter) in einer Regentonne in Abhängigkeit von der Zeit t (in Minuten) gemessen:
Übertrage die Messdaten in das Koordinatensystem und kennzeichne die mittlere Volumenänderung durch ein Steigungsdreieck.  |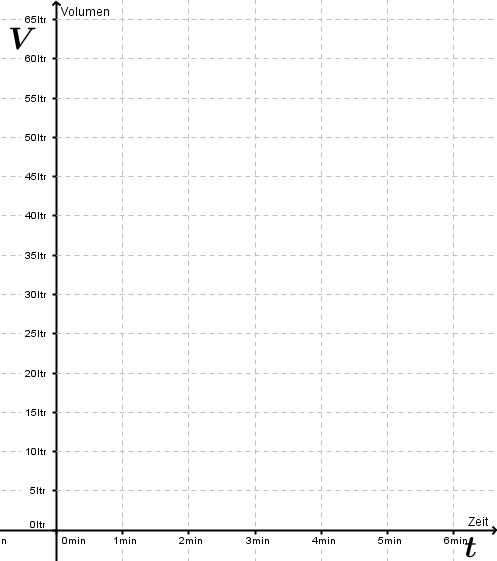
||||||||||||
 |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2
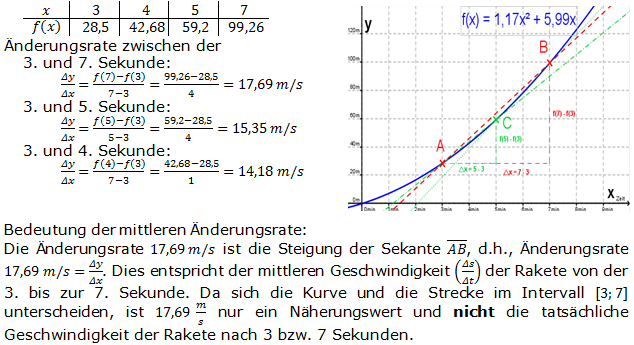
| Die Flughöhe einer Rakete nach dem Start hängt von der Zeit ab. Für eine Saturn-V-Rakete kann die Flugbahn (in Metern) näherungsweise durch die Funktion f(x)=1,17x2+5,99x in Abhängigkeit von der Zeit x (in Sekunden) beschrieben werden. Berechne die Änderungsrate der 3. und 7. Sekunde, der 3. und 5. Sekunde, der 3. und 4. Sekunde. Interpretiere diese Änderungsraten. |
| Eine Frage stellen... |
Aufgabe A3 (4 Teilaufgaben)
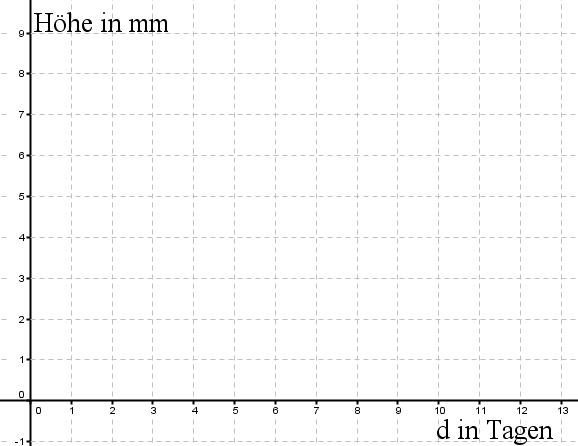
| Die Höhe einer Kresse Pflanze wurde über mehrere Tage bestimmt (siehe Tabelle). | |||||||||||||||||||||
 |
|
||||||||||||||||||||
|
|
|||||||||||||||||||||
| Trage die Messpunkte in das Koordinatensystem ein und verbinde sie mit einer Kurve. Berechne dann die mittlere Änderungsrate der Funktion Tage ⟶ Höhe für
|
|||||||||||||||||||||
| Eine Frage stellen... |
Aufgabe A4 (4 Teilaufgaben)
| Bei einer Bakterienkultur verdoppelt sich jede Stunde die Anzahl der Bakterien. Zu Beginn der Messung waren etwa 12000 Bakterien vorhanden. Bestimme die mittlere Änderungsrate der Bakterienzahl für das angegebene Intervall I.
|
| Eine Frage stellen... |
| Du befindest dich hier: |
| Mittlere Änderungsrate - Level 2 - Fortgeschritten - Blatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
