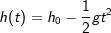 Wie wir in den beiden Beispielen gesehen haben, verändert sich die mittlere Änderungsrate je nachdem, zwischen welchen Messpunkten wir sie berechnen. Nun lassen sich solche Messreihen auch durch mathematische Funktionen beschreiben, denen eine Funktions-gleichung zugrunde liegt. Wie wir in den beiden Beispielen gesehen haben, verändert sich die mittlere Änderungsrate je nachdem, zwischen welchen Messpunkten wir sie berechnen. Nun lassen sich solche Messreihen auch durch mathematische Funktionen beschreiben, denen eine Funktions-gleichung zugrunde liegt.
Betrachten wir uns einmal die h-t–Funktion des freien Falls. Ihre Funktionsgleichung lautet ja
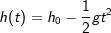
mit g=9,81 m/s2 als Erdbeschleunigung (Ortsfaktor).
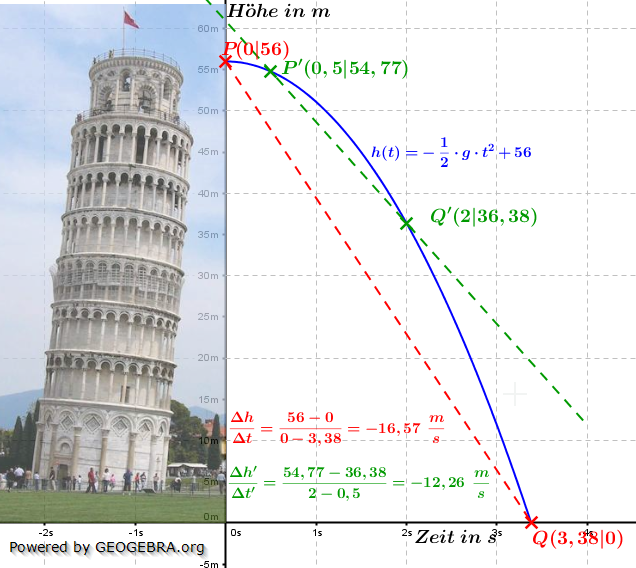
Wir lassen einen Stein vom schiefen Turm in Pisa aus rund h0=56 m Höhe herunterfallen. Der Graph der Funktion des freien Falls ist ja eine Parabel wie obenstehend abgebildet. Die Fallgeschwindigkeit des Steins wird ja stets größer, bis er auf der Erde aufschlägt. Nun wollen wissen, mit welcher Durchschnittsgeschwindigkeit der Stein fällt, bilden also den Differenzenquotienten zwischen den Punkten P und Q, also in I=[0;3,38]. Die Berechnung zeigt, dass wir eine mittlere Fallgeschwindigkeit von 16,57 m/s haben.
Bei der Fallstrecke zwischen den Punkten P' und Q', also in I=[0,5;2], kommen wir zu einer mittleren Fallgeschwindigkeit von 12,26 m/s. (Dass die Geschwindigkeiten in der Grafik mit „-„ angegeben sind, rührt daher, dass der Stein ja nach unten fällt.)
Betrachten wir uns noch einmal die obige Grafik. Die rote Linie für I=[0;3,38] schneidet ja den Graphen der h-t–Funktion in den Punkten P und Q. Sie ist also, bezüglich des Graphen eine Sekante. Gleiches gilt auch für die grüne Linie mit den Punkten P' und Q', sie ist ebenfalls eine Sekante. Sekanten sind im mathematischen Sinne Geraden und über den Differenzenquotienten haben wir die Steigung dieser Geraden berechnet.
Mit anderen Worten: |





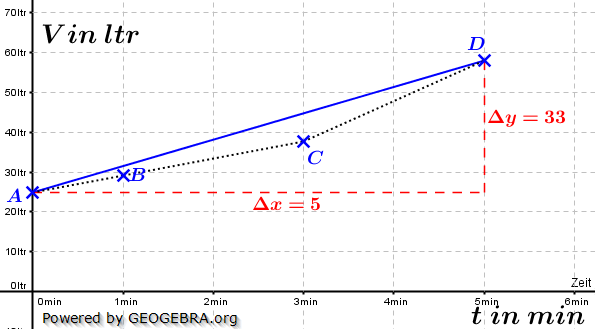
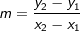
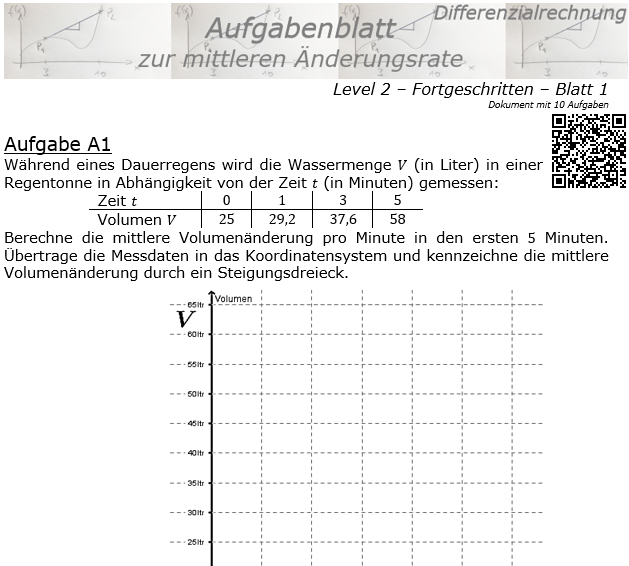
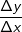 . Um den Bereich zu beschreiben, für den wir die mittlere Änderungsrate bestimmen wollen, schreiben wir I=[a;b] (gesprochen „Im Intervall von a bis b“). In unserem Beispiel ist a=0 und b=5. Mithilfe dieser Definitionen können wir nun die mittlere Änderungsrate (die ja eine Änderungsrate des Volumens ist) berechnen mit:
. Um den Bereich zu beschreiben, für den wir die mittlere Änderungsrate bestimmen wollen, schreiben wir I=[a;b] (gesprochen „Im Intervall von a bis b“). In unserem Beispiel ist a=0 und b=5. Mithilfe dieser Definitionen können wir nun die mittlere Änderungsrate (die ja eine Änderungsrate des Volumens ist) berechnen mit: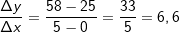
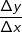 .
. 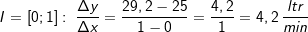
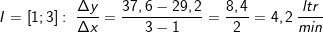
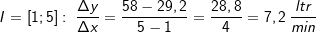
 Wie wir in den beiden Beispielen gesehen haben, verändert sich die mittlere Änderungsrate je nachdem, zwischen welchen Messpunkten wir sie berechnen. Nun lassen sich solche Messreihen auch durch mathematische Funktionen beschreiben, denen eine Funktions-gleichung zugrunde liegt.
Wie wir in den beiden Beispielen gesehen haben, verändert sich die mittlere Änderungsrate je nachdem, zwischen welchen Messpunkten wir sie berechnen. Nun lassen sich solche Messreihen auch durch mathematische Funktionen beschreiben, denen eine Funktions-gleichung zugrunde liegt.