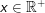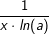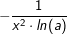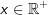|
|
Die Ableitungen in der Differenzialrechnung
|


Die Ableitungen - Einleitung
| Im Portalbereich „Änderungsraten“ haben wir bereits kennengelernt, dass man den Grenzwert des Differenzenquotienten für minimale Δx als Differenzialquotienten bezeichnet und dass dieser Differenzialquotient gleichbedeutend ist mit dem Begriff „Ableitung“. Mittels mathematischer Umformungen haben wir den Differenzenquotienten in den Differenzialquotienten (die Ableitung) in einem bestimmten Punkt des Graphen einer Funktion überführt. Diese mathematischen Umformungen waren mehr oder weniger umständlich. | ||
| Nun fragen wir uns natürlich, ob diese umständliche Berechnung nicht einfacher und eleganter erfolgen kann und vor allem nicht in einem ganz bestimmten Punkt, sondern generell für alle Punkte des Graphen einer beliebigen Funktion. Mit diesem Thema beschäftigen wir uns nun im Portalbereich „Ableitungen“ und wir rekapitulieren noch einmal kurz, wie die Ableitung mathematisch formuliert wird. |
||
|
Differenzierbarkeit und Stetigkeit
Die Ableitung f' einer Funktion f an der Stelle x0 kann jedoch nur gebildet werden, wenn die Funktion f dort differenzierbar und stetig ist. Mehr hierzu erfährst du im Untermenü „Differenzierbarkeit und Stetigkeit“ (linkes Menü).Grafisches Differenzieren
Bevor wir uns mit den (rechnerischen) Ableitungsregeln beschäftigen, lernen wir hier, wie man aus dem Graphen einer Funktion f den Graphen ihrer Ableitung f' erhält. Dies ist ins besonders dann erforderlich, wenn zu dem Graphen von f keine Funktionsgleichung f(x) vorliegt. Mehr hierzu erfährst du im Untermenü „Grafisches Differenzieren“ (linkes Menü).Die Ableitungsregeln
Je nach Art und Ausprägung einer Funktion müssen wir unterschiedliche Ableitungsregeln einsetzen. Diese sind nachfolgend global beschrieben. Mehr zu den Regeln erfährst du in den entsprechenden Untermenüpunkten (linkes Menü).Die Konstantenregel
Die Konstantenregel besagt, dass Konstanten bei der Ableitung verloren gehen.Beispiel: f(x)=5 f'(x)=0
Die Faktorregel
Die Faktorregel besagt, dass Faktoren bei der Ableitung unverändert beibehalten werden.Beispiel: f(x)=a⋅x f'(x)=a
Die Potenzregel
Bei der Potenzregel (Ableitungsregel für Potenzfunktionen) wird der Exponent von x als Multiplikand vor die Ableitung geschrieben und der Exponent um 1 vermindert.Beispiel: f(x)=xn f'(x)=n⋅xn-1
Die Summen- bzw. Differenzregel
Die Summen- bzw. Differenzregel besagt, dass bei additiv bzw. subtraktiv zusammengesetzten Funktionen jedes Glied der zusammengesetzten Funktion einzeln abgeleitet wird.Beispiel: f(x)=g(x)+h(x)-i(x) f'(x)=g'(x)+h'(x)-i'(x)
Die Produktregel
Sind einzelne Funktionsglieder multiplikativ miteinander verknüpft, so muss für die Ableitung die Produktregel angewandt werden.Beispiel: f(x)=g(x)⋅h(x) f'(x)=g'(x)⋅h(x)+g(x)⋅h'(x)
Die Quotientenregel
Sind einzelne Funktionsglieder mittels Division miteinander verknüpft, so muss für die Ableitung die Quotientenregel angewandt werden.Beispiel:
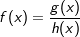
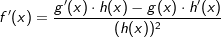
Die Kettenregel
Sind zwei Funktionen miteinander verkettet, so muss für die Ableitung die Kettenregel angewandt werden.Beispiel: f(x)=g(h(x)) f'(x)= g'(h(x))⋅h'(x)
Ableitung der trigonometrischen Funktionen
Die Ableitungsregeln der trigonometrischen Funktionen lauten:f(x)=sin(x) f'(x)=cos(x)
f(x)=cos(x) f'(x)=-sin(x)
f(x)=tan(x)

Ableitung der Exponentialfunktion
Die Ableitungsregel der Exponentialfunktion lautet:f(x)=ex f'(x)=ex
f(x)=ax f'(x)=ax⋅ln(a)
Ableitung der Logarithmusfunktion
Die Ableitung der Logarithmusfunktion lautet:f(x)=ln(x)
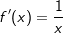
f(x)=loga(x)
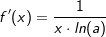
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 08. September 2019 08. September 2019


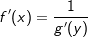
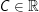 , constant
, constant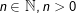
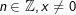
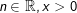
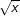
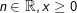
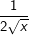
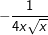
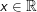
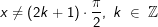
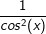
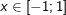
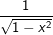
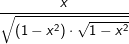
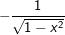
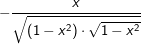
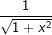
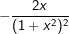
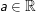 , a>0; a≠1
, a>0; a≠1