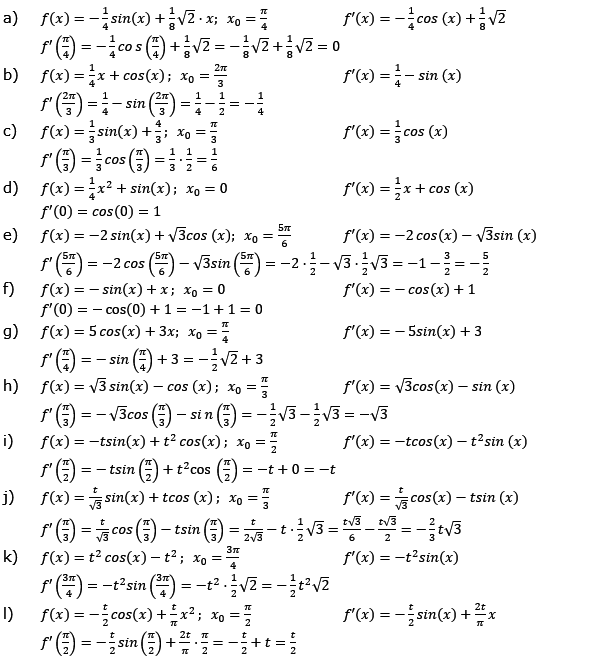 |
Ableitung trigonometrische Funktionen - Level 2 - Fortgeschritten - Blatt 1 |
| Dokument mit 30 Aufgaben |
Fehler melden...Aufgabe A2 (12 Teilaufgaben)
Bestimme den exakten Wert der Steigung des Graphen von f an der Stelle x0. |
 Eine Frage stellen... |
Aufgabe A3 (3 Teilaufgaben)
In welchem Punkt hat der Graph von f mit f(x)=sin(x) im Intervall [0;2π] dieselbe![In welchem Punkt hat der Graph von f mit f(x)=sin(x) im Intervall [0;2π] dieselbe (Grafik A210301 im Aufgabensatz 3 Blatt 2/1 Fortgeschritten zur Ableitung trigonometrischer Funktionen /© by www.fit-in-mathe-online.de)](/images/analysis/differenzialrechnung/ableitungen/trigonometrische-funktionen/A210301.png "In welchem Punkt hat der Graph von f mit f(x)=sin(x) im Intervall [0;2π] dieselbe (Grafik A210301 im Aufgabensatz 3 Blatt 2/1 Fortgeschritten zur Ableitung trigonometrischer Funktionen)") |
| Eine Frage stellen... |
Aufgabe A4 (2 Teilaufgaben)
Gegeben ist die Funktion f mit f(x)=sin(x) im Intervall [0;2π].![Gegeben ist die Funktion f mit f(x)=sin(x) im Intervall [0;2π]. (Grafik A210401 im Aufgabensatz 4 Blatt 2/1 Fortgeschritten zur Ableitung trigonometrischer Funktionen /© by www.fit-in-mathe-online.de)](/images/analysis/differenzialrechnung/ableitungen/trigonometrische-funktionen/A210401.png "Gegeben ist die Funktion f mit f(x)=sin(x) im Intervall [0;2π]. (Grafik A210401 im Aufgabensatz 4 Blatt 2/1 Fortgeschritten zur Ableitung trigonometrischer Funktionen)") |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Ableitung trigonometrische Funktionen Level 2 - Fortgeschritten - Blatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
