|
|
Differenzialrechnung - Grafisches Differenzieren |


Grafisches Differenzieren - Einführung
| Grafisches Differenzieren (auch grafische Ableitung genannt) gibt uns zum einen die Möglichkeit, die Steigung des Graphen einer Funktion f in einem bestimmten Punkt P(x0|y0) zu ermitteln, ohne dass wir die Funktionsgleichung f(x) des Graphen von f kennen, zum anderen können wir damit auch den Verlauf des Graphen der Ableitung f' skizzieren. Umgekehrt gilt dies auch für das Skizzieren des Graphen einer Funktion f aus dem Verlauf des Ableitungsgraphen f'. Letzteres wird dann nicht mehr „Grafisches Differenzieren“ genannt, sondern „Grafisches Integrieren“. Um grafisches Differenzieren zu lernen, kannst du dir den nachfolgenden Video ansehen, oder aber du liest dir die verbalen Beschreibungen im Einzelnen durch. |
Regeln und Beispiele
Steigung in einem bestimmten Punkt
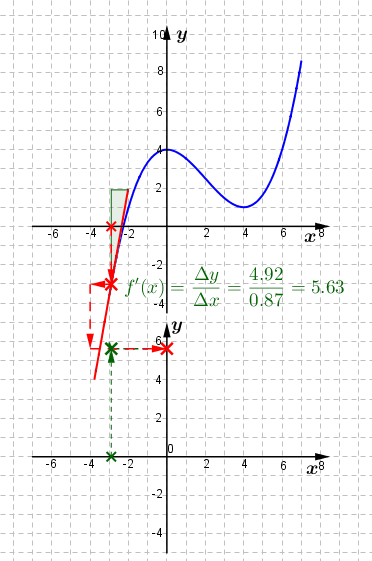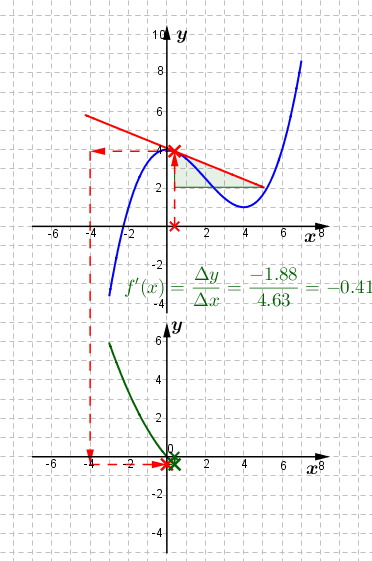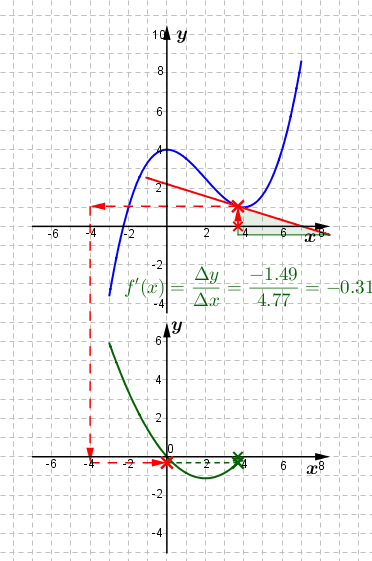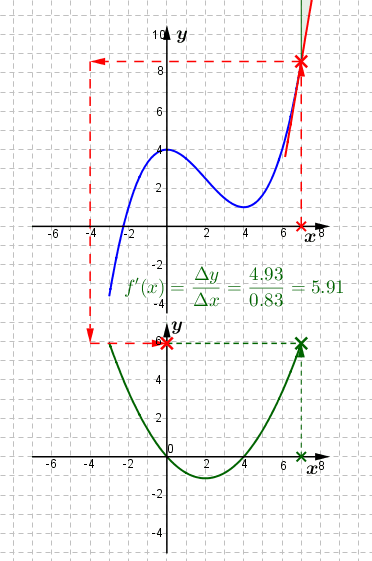
Hierzu müssen wir in dem bestimmten Punkt zeichnerisch eine Tangente an die zu untersuchende Kurve legen, wie in der nachfolgenden Grafik dargestellt.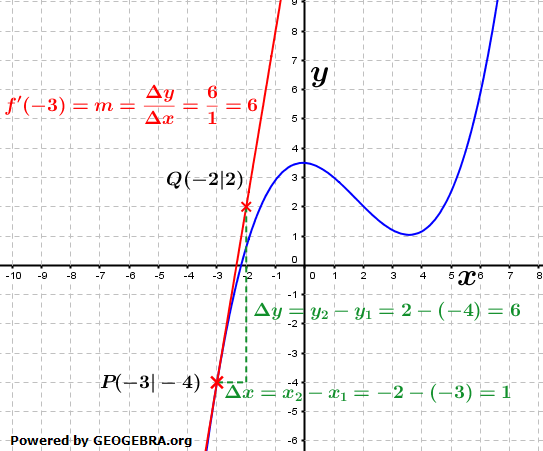 Wir wollen die Steigung der Kurve, deren Funktions-gleichung wir nicht kennen, an der Stelle x0=-3 bestimmen. Wir tragen den Punkt P ein und stellen fest, dass der zugehörige y-Wert gleich -4 ist. Jetzt zeichnen wir eine Tangente an die Kurve im Punkt P(-3|-4). Als nächstes suchen wir auf der eingezeichneten Tangente einen weiteren, gut ablesbaren Punkt und stellen fest, dass dieser Punkt bei Q(-2|2) liegt. Wir wollen die Steigung der Kurve, deren Funktions-gleichung wir nicht kennen, an der Stelle x0=-3 bestimmen. Wir tragen den Punkt P ein und stellen fest, dass der zugehörige y-Wert gleich -4 ist. Jetzt zeichnen wir eine Tangente an die Kurve im Punkt P(-3|-4). Als nächstes suchen wir auf der eingezeichneten Tangente einen weiteren, gut ablesbaren Punkt und stellen fest, dass dieser Punkt bei Q(-2|2) liegt.Wir tragen an die Tangente ein Steigungsdreieck ein (in obiger Grafik grün gezeichnet) und erhalten damit die Differenz Δx der x-Koordinaten und Δy der y-Koordinaten von P und Q. Zum Schluss berechnen wir die Steigung, indem wir Δy/Δx bilden. Im Beispiel erhalten wir den Wert 6. Also ist die Steigung m der Tangente gleich 6 und damit die Steigung f'(-3) der Kurve ebenfalls 6. |
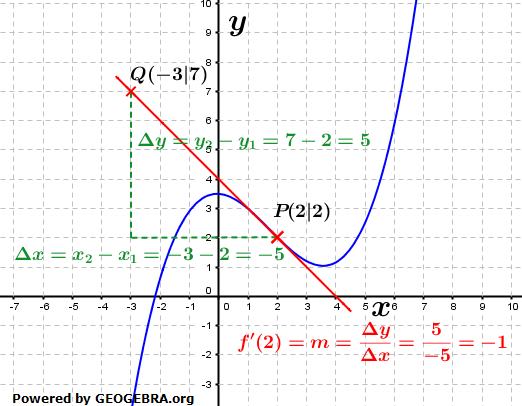 Die seitliche Grafik stellt den gleichen Zusammenhang für den Ausgangspunkt P(2|2) der Kurve dar. Die seitliche Grafik stellt den gleichen Zusammenhang für den Ausgangspunkt P(2|2) der Kurve dar.Die Suche nach einem zweiten, gut ablesbaren Punkt auf der Tangente durch den Punkt P(2|2) führt uns zu Q(-3|7). Wir bilden wieder die Differenzen Δx und Δy, stellen den Quotienten Δy/Δx auf und erhalten damit die Steigung der Tangente mit m=-1 sowie die Steigung der Kurve in P(2|2) ebenfalls mit f'(2)=-1. |
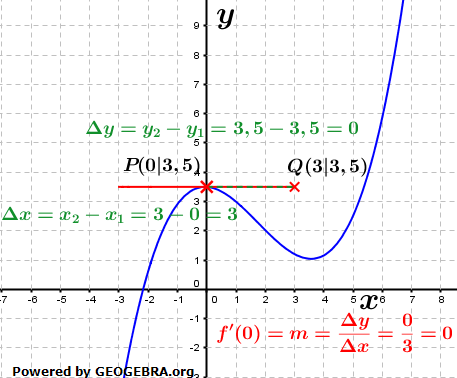 Als letztes interessiert uns noch ein besonderer Punkt, nämlich der Punkt der Kurve bei x0=0. Als letztes interessiert uns noch ein besonderer Punkt, nämlich der Punkt der Kurve bei x0=0.Wie wir sehen, erhalten wir für die Differenz Δy der y-Werte den Wert 0. Dies bedeutet, dass dort die Tangente an die Kurve als auch die Kurve selbst keine Steigung haben, bzw. f'(0)=m=0 ist. Solche Stellen, in denen offenbar eine positive Steigung in eine negative Steigung übergeht, bezeichnen wir als Extremstellen einer Kurve. Wechselt in einer Extremstelle die Steigung von positiv nach negativ, sprechen wir von einem Hochpunkt. Wechselt die Steigung hingegen von negativ nach positiv, so haben wir es mit einem Tiefpunkt zu tun. |
Graphen der Ableitungsfunktion skizzieren
| In der oben ablaufenden Animation wird dies im Intervall I=[-3;6] in 0,1-er Schritten ausgeführt. In der Mitte der Animation kannst du Schritt für Schritt sehen, wie sich die einzelnen Steigungen f'(x) verändern. Im unteren Koordinatensystem entsteht so schrittweise der Graph der Ableitungsfunktion f'. Wie wir sehen, ein aufwändiges Verfahren. Um so etwas jedoch schneller bewerkstelligen zu können, bedienen wir uns lediglich einiger markanter Punkte unserer Ausgangskurve, wie du im nachfolgenden Slider nachlesen kannst. |
Markante Punkte
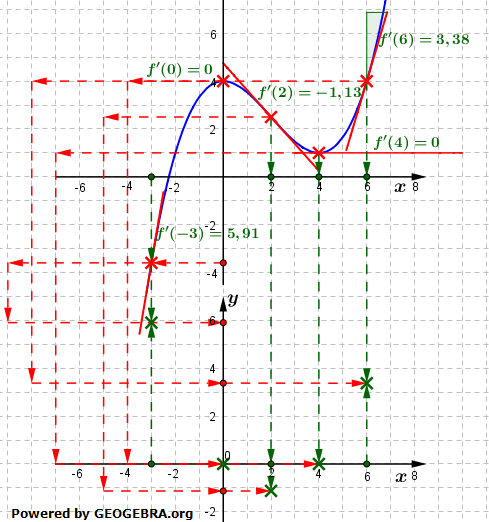 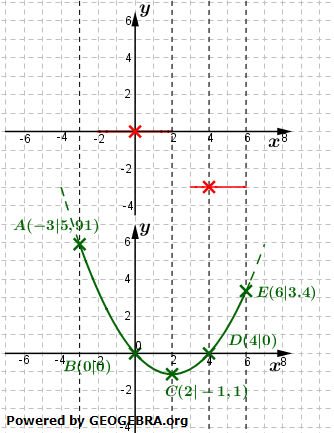 Betrachte dir hierzu die nebenstehende Grafik und die einzelnen Erläuterungen hierzu. Betrachte dir hierzu die nebenstehende Grafik und die einzelnen Erläuterungen hierzu.Als markante Punkte wählen wir die folgenden Stellen:
|
Graphen der Stammfunktion skizzieren
| Jetzt kommt es aber auch vor, dass wir den Graphen der Ableitungsfunktion vorgegeben haben und wollen wissen, wie wohl der Graph der Ursprungsfunktion aussieht. Für diese Ursprungsfunktion hat der Mathematiker wieder einen neuen Begriff geschaffen und nennt diese Funktion die „Stammfunktion“. |
| Wir betrachten uns nun dasselbe Beispiel wie zuvor, gehen dabei aber von der (un)bekannten Ableitungsfunktion aus. Wir verwenden wieder dieselben markanten Punkte A bis E. Als erstes zeichnen wir nun ein paar senkrechte Linien durch die Punkte. Irgendwo auf diesen Linien muss der entsprechende Punkt der Stammfunktion liegen und dort die Steigung gemäß dem y-Wert der Punkte haben. Am einfachsten sind wohl die Punkte B und D, denn dort ist die Steigung ja 0, die Stammfunktion muss dort eine Extremstelle besitzen. Betrachten wir zunächst die Stelle x0=0. In dieser Nullstelle wechselt das Vorzeichen der Ableitungsfunktion von „+“ nach „-". Dies bedeutet, dass in x0=0 die Stammfunktion einen Hochpunkt besitzt. Da wir aber nicht mehr genau wissen, in welcher Höhe dieser Hochpunkt liegt, tragen wir die waagrechte Tangente einfach auf der x-Achse liegend ein. Bezüglich der Nullstelle bei x0=4 liegt ein Vorzeichenwechsel von „-" nach „+" vor, d.h., die Stammfunktion muss dort einen Tiefpunkt haben. | 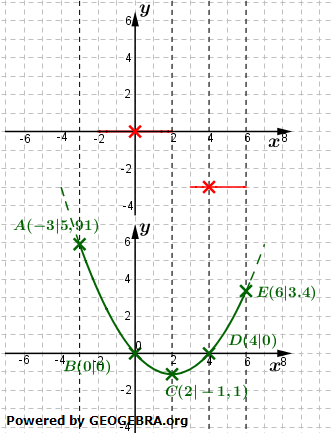 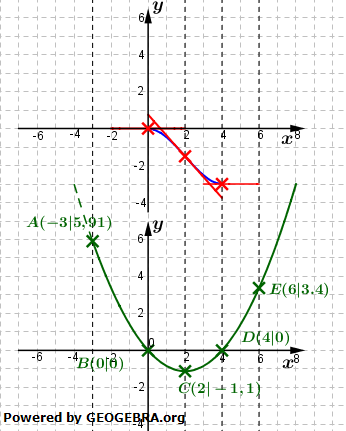 |
| Da bei x0=0 ein Hochpunkt ist, muss der Kurvenpunkt bei x0=4 unterhalb der x-Achse liegen. Wir zeichnen also eine waagrechte Tangente (bei etwa y=-3, siehe Grafik) ein. Nun betrachten wir die Stelle bei x0=2. Über die y-Koordinate des Punktes C wissen wir, dass die Stammfunktion bei x0=2 eine Steigung von -1,1 haben muss. Wir tragen eine Tangente mit der Steigung m=-1,1 etwa in halber y-Höhe zwischen x0=0 und x0=4 ein. Jetzt können wir die Stammfunktion zwischen x0=0 und x0=4 schon skizzieren. | |
| Es verbleiben jetzt lediglich noch die Stellen bei x0=-3 und x0=6. Die y-Koordinate der Punkte A und B sagt aus, dass die Stammfunktion dort positive Steigung haben muss, nämlich m=5,9 bei x0=-3 und m=3,4 bei x0=6. Wegen des Hochpunktes bei x0=0 und der positiven Steigung muss die y-Koordinate bei x0=-3 somit unterhalb der x-Achse liegen. Wegen des Tiefpunktes bei x0=4 und der positiven Steigung m=3,4 muss die y-Koordinate bei x0=6 somit oberhalb der y-Koordinate des Tiefpunktes bei x0=4 liegen. | 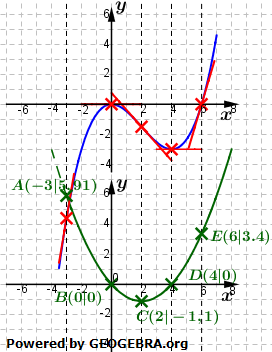 |
| Wir zeichnen die beiden Tangenten an den entsprechenden Stellen ein (siehe Grafik) und verbinden dann lediglich das bereits eingezeichnete Teilstück zwischen x0=0 und x0=4 mit den seitlichen Punkten. Die Grafik unserer Stammfunktion ist somit skizziert. Wie wir nun aber erkennen können, liegt unsere Stammfunktion tiefer, als bei der graphischen Ermittlung der Ableitungsfunktion im ersten Teil unserer Betrachtung. Dies rührt daher, als durch die Ableitung eine wesentliche Information der Stammfunktion verloren geht, nämlich die Information, um wie viele Einheiten die Stammfunktion in y-Richtung verschoben ist. |
|
Die 'NEW'-Regel
| Die sogenannte „NEW-Regel“ ist eine der wichtigsten Regeln für grafisches differenzieren und integrieren. Die Abkürzung „NEW“ hat dabei nichts mit dem englischen Wort „new“ = neu zu tun. In der Abkürzung „NEW“ bedeutet: N = Nullstelle E = Extremstelle W = Wendepunkt Mit der NEW-Regel kannst du 90 % und mehr solcher Aufgaben ohne große Schwierigkeiten lösen. |
Die "NEW"-Regel
 |
||||||||||||||||||||
| NVZW=Nullstelle mit Vorzeichenwechsel, E=Extremstelle, W=Wendestelle F(x)=Stammfunktion, f(x)=1. Ableitung von F, f'(x)=2. Ableitung von F, f''(x)=3. Ableitung von F |
||||||||||||||||||||
| Weiterhin gilt: | ||||||||||||||||||||
|
| Die NEW-Regel liest sich wie folgt: Beim grafischen Differenzieren: |
| Hat die Ausgangsfunktion F eine Nullstelle (mit VZW) kann bezüglich der weiteren Ableitungen keine Aussage getroffen werden. Hat die Ausgangsfunktion F eine Extremstelle (Hoch- bzw. Tiefpunkt), so hat ihre erste Ableitung eine Nullstelle (mit Vorzeichenwechsel), über weitere Ableitungen kann keine Aussage getroffen werden. Hat die Ausgangsfunktion F eine Wendestelle, so hat ihre erste Ableitung eine Extremstelle (Hoch- bzw. Tiefpunkt), die zweite Ableitung eine Nullstelle (mit Vorzeichenwechsel) und die dritte Ableitung ist ungleich 0. Ist die dritte Ableitung größer als 0, so wechselt der Graph der Funktion F von rechtsdrehend auf linksdrehend. Ist die dritte Ableitung kleiner als 0, so wechselt der Graph der Funktion F von linksdrehend auf rechtsdrehend. |
| Beim grafischen Integrieren: |
| Hat die Ableitungsfunktion f einen Wendepunkt, kann bezüglich der Stammfunktion F keine Aussage getroffen werden. Hat die Ableitungsfunktion f eine Extremstelle (Hoch- bzw. Tiefpunkt), so hat die Stammfunktion F eine Wendestelle. Hat die Ableitungsfunktion f eine Nullstelle (mit Vorzeichenwechsel), so hat die Stammfunktion F einen Extrempunkt. Wechselt das Vorzeichen in der Nullstelle von "+" nach "-", so ist diese Extremstelle ein Hochpunkt. Wechselt das Vorzeichen in der Nullstelle von "-" nach "+", so ist diese Extremstelle ein Tiefpunkt. |
Beispiele
Beispiel 1
Ordne den Graphen A), B), C) und D) die Graphen der dazugehörigen Ableitungsfunktionen 1), 2), 3) und 4) zu.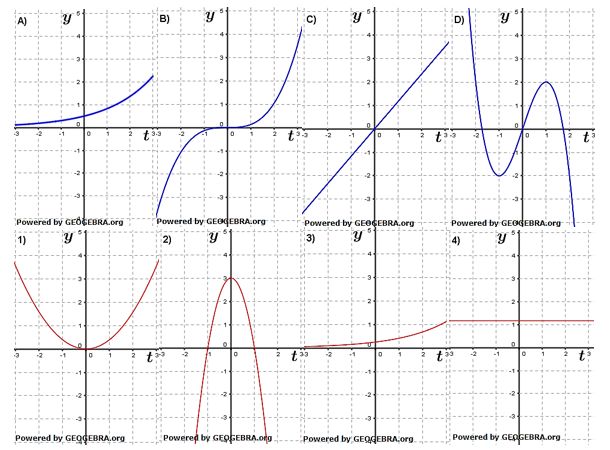 |
Lösung 1
| Zum Graphen A) gehört Ableitungsgraph 3). Graph A) hat weder Extremstellen noch Wendepunkte. Er ist in 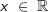 streng monoton steigend, deshalb muss sein Ableitungsgraph in streng monoton steigend, deshalb muss sein Ableitungsgraph in 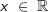 oberhalb der x-Achse verlaufen. oberhalb der x-Achse verlaufen. |
| Zum Graphen B) gehört Ableitungsgraph 1). Graph B) hat in x0=0 eine Wendestelle, die im Ableitungsgraph zu einer Extremstelle wird. Graph B) ist in 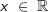 streng monoton steigend, deshalb muss sein Ableitungsgraph in streng monoton steigend, deshalb muss sein Ableitungsgraph in 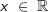 oberhalb der x-Achse verlaufen. oberhalb der x-Achse verlaufen. |
| Zum Graphen C) gehört Ableitungsgraph 4). Graph C) hat weder Extremstellen noch Wendepunkte. Seine Steigung ist in 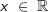 gleich (lineare Funktion) und m>0, deshalb muss sein Ableitungsgraph parallel zur x-Achse verlaufen. gleich (lineare Funktion) und m>0, deshalb muss sein Ableitungsgraph parallel zur x-Achse verlaufen. |
| Zum Graphen D) gehört Ableitungsgraph 2). Graph D) hat zwei Extremstellen, die im Ableitungsgraphen zu Nullstellen mit Vorzeichenwechsel führen. Graph D) hat einen Wendepunkt, der im Ableitungsgraph zu einer Extremstelle führt. |
Beispiel 2
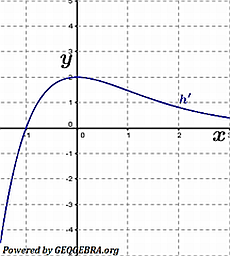
h ist eine in 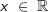 differenzierbare Funktion. Nebenstehend ist für -1,5≤x≤3 das Schaubild ihrer Ableitungsfunktion h' dargestellt. differenzierbare Funktion. Nebenstehend ist für -1,5≤x≤3 das Schaubild ihrer Ableitungsfunktion h' dargestellt.Entscheide, ob die folgenden Aussagen über die Funktion h richtig, falsch oder unentscheidbar sind. Begründe deine Entscheidung. |
 |
|
| (1) | An der Stelle x=-1 hat das Schaubild von h einen Tiefpunkt. | |
| (3) | An der Stelle x=0 hat das Schaubild von h eine Tangente, die parallel ist zur Geraden mit der Gleichung y=2x-7. | |
| (4) | h ist streng monoton wachsend für -1,5≤x≤0. | |
Lösung 2
| (1) | Die Aussage ist wahr. h' hat an der Stelle x=-1 eine Nullstelle mit VZW von - nach +. |
| (2) | Die Aussage ist unentscheidbar, da jede Funktion f mit f(x)=h(x)+C eine Stammfunktion von h' ist. |
| (3) | Die Aussage ist wahr. h'(0)=2 (siehe Grafik). Somit hat h an der Stelle x=0 die Steigung m=2. |
| (4) | Die Aussage ist falsch. h' verläuft im Intervall -1,5≤x≤-1 unterhalb der x-Achse, somit ist h in diesem Intervall monoton fallend. |
| Weiterführende Informationen zu diesem Thema findest du im Kapitel „Analysis/Differenzialrechnung/Grafisches Differenzieren und Integrieren“. |
| Titel Aufgabenblatt | Level / Blattnr. |
Grafisches Differenzieren Level 1 / Blatt 1 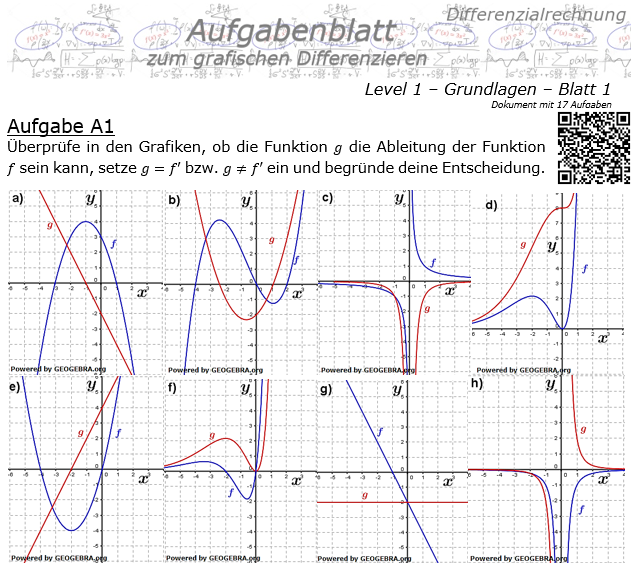 17 Aufgaben im Blatt |
Grafisches Differenzieren Level 1 / Blatt 2 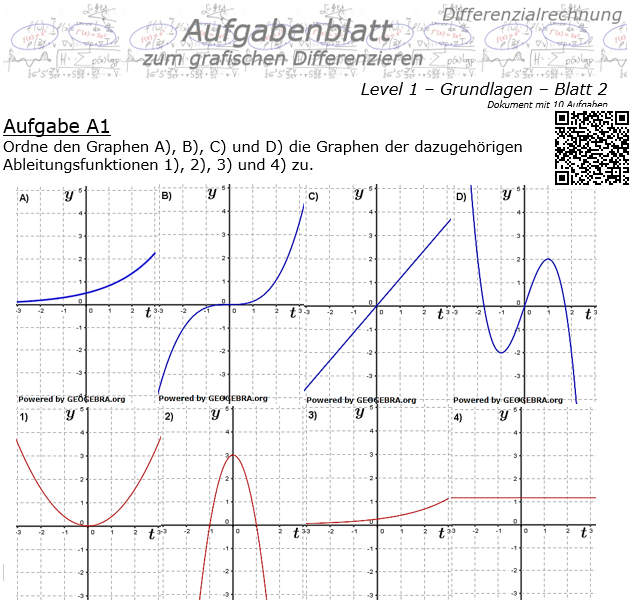 10 Aufgaben im Blatt |
Grafisches Differenzieren Level 1 / Blatt 3 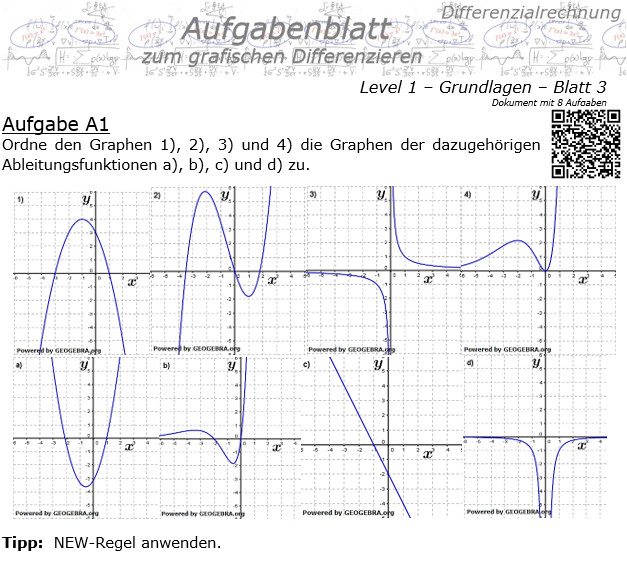 8 Aufgaben im Blatt |
Grafisches Differenzieren Level 2 / Blatt 1 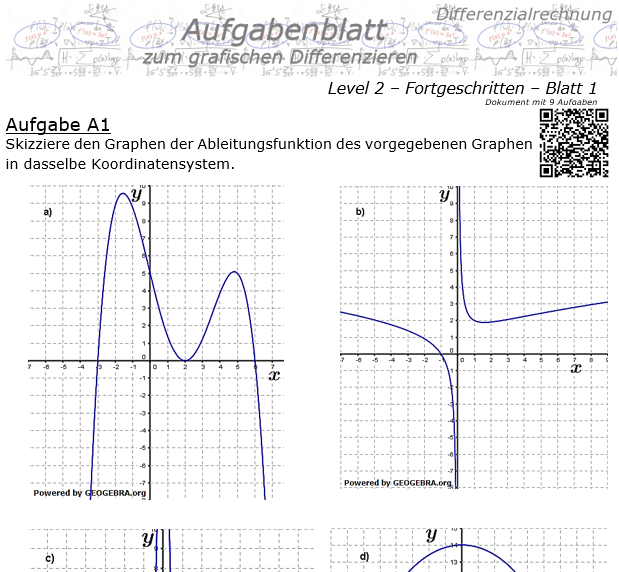 9 Aufgaben im Blatt |
Grafisches Differenzieren Level 2 / Blatt 2  13 Aufgaben im Blatt |
Grafisches Differenzieren Level 3 / Blatt 1  33 Aufgaben im Blatt |
Grafisches Differenzieren Level 3 / Blatt 2  20 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 23. November 2021 23. November 2021