| Zur Bildung der Ableitung von Funktionen wie |
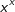 |
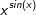 |
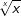 |
| können wir keine der bis jetzt bekannten Ableitungsregeln direkt anwenden, da die Variable sowohl in der Basis als auch im Exponenten auftritt. Trotzdem gelingt die Differentiation dieser Funktionen, wenn wir die Funktionsgleichung zunächst logarithmieren. |
| Aus |
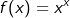 mit x>0 mit x>0 |
| erhalten wir durch Logarithmieren beider Seiten der Gleichung |
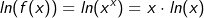 |
| Die so entstandene Funktionsgleichung können wir nun nach den bekannten Regeln ableiten, in unserem Falle die Ableitung des ln auf der linken Gleichungsseite und der Produktregel auf der rechten Gleichungsseite. |
Betrachten wir zunächst die linke Gleichungsseite mit 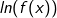 . Die Ableitung von . Die Ableitung von 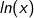 ist ja ist ja  . Jetzt haben wir aber nicht . Jetzt haben wir aber nicht 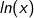 sondern sondern 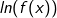 , sodass wir zusätzlich noch die Kettenregel benötigen. Somit ist die Ableitung , sodass wir zusätzlich noch die Kettenregel benötigen. Somit ist die Ableitung |
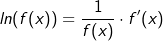 |
Jetzt betrachten wir die rechte Gleichungsseite. Dort steht ja nach dem Logarithmieren 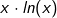 , wofür wir ja die Produktregel benötigen. Also: , wofür wir ja die Produktregel benötigen. Also: |
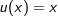 |
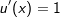 |
|
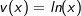 |
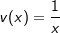 |
|
| Nach der Produktregel bilden wir nun u'(x)∙v(x)+v'(x)∙u(x). Dies führt zu: |
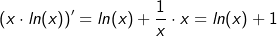 |
| Nun haben wir beide Seiten der logarithmieren Gleichung abgeleitet und haben somit: |
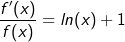 |
Da wir aber nicht wissen wollen, was 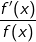 sondern was f'(x) ist, müssen wir die Gleichung noch mit f(x) multiplizieren. Dadurch erhalten wir: sondern was f'(x) ist, müssen wir die Gleichung noch mit f(x) multiplizieren. Dadurch erhalten wir: |
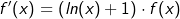 |
Und da ja 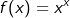 ist, letztendlich ist, letztendlich |
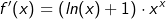 |




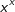
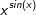
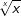
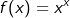 mit x>0
mit x>0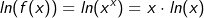
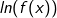 . Die Ableitung von
. Die Ableitung von 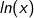 ist ja
ist ja  . Jetzt haben wir aber nicht
. Jetzt haben wir aber nicht 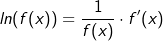
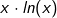 , wofür wir ja die Produktregel benötigen. Also:
, wofür wir ja die Produktregel benötigen. Also: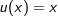
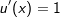
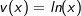
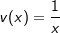
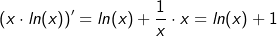
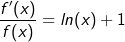
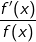 sondern was f'(x) ist, müssen wir die Gleichung noch mit f(x) multiplizieren. Dadurch erhalten wir:
sondern was f'(x) ist, müssen wir die Gleichung noch mit f(x) multiplizieren. Dadurch erhalten wir: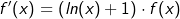
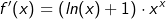
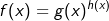
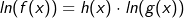
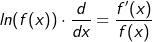
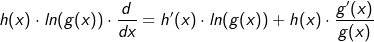
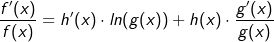
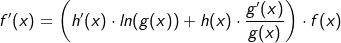
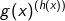 sowie g(x) und h(x) in ganz
sowie g(x) und h(x) in ganz 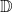 differenzierbar und g(x) > 0, so gilt für die Ableitung von f
differenzierbar und g(x) > 0, so gilt für die Ableitung von f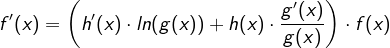
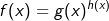
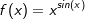 .
.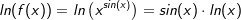 .
.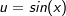
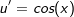
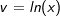
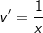
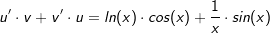
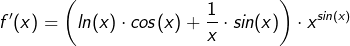






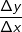 für Δx⟶0.
für Δx⟶0.