|
|
Die Ableitung der Logarithmusfunktion (Umkehrregel) |


Merksatz Ableitung der Logarithmusfunktion (Umkehrregel)
Ist x=g(y)die Umkehrfunktion von y=f(x), so gilt 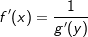 . .Die Ableitung der Logarithmusfunktion mit f(x)=ln(x) lautet 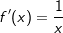 . .Die Ableitung der Logarithmusfunktion mit f(x)=loga(x) lautet 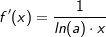 . . |
| Titel Aufgabenblatt | Level / Blattnr. |
| Ableitung Logarithmusfunktion (Umkehrregel) Aufgabenblatt Level 1/Blatt 1 20 Aufgaben im Blatt |
| Ableitung Logarithmusfunktion (Umkehrregel) Aufgabenblatt Level 1/Blatt 2 34 Aufgaben im Blatt |
| Ableitung Logarithmusfunktion (Umkehrregel) Aufgabenblatt Level 2/Blatt 1 20 Aufgaben im Blatt |
| Ableitung Logarithmusfunktion (Umkehrregel) Aufgabenblatt Level 2/Blatt 2 20 Aufgaben im Blatt |
| Ableitung Logarithmusfunktion (Umkehrregel) Aufgabenblatt Level 3/Blatt 1 2 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

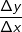 für Δx⟶0.
für Δx⟶0.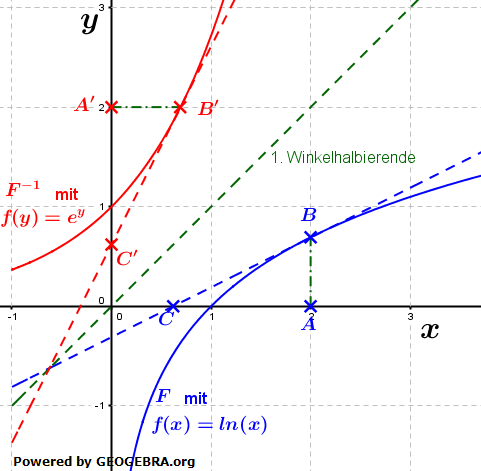 In der Grafik erkennen wir, dass die Steigung der Tangente an F-1 sich aus
In der Grafik erkennen wir, dass die Steigung der Tangente an F-1 sich aus 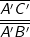 bildet, die Steigung der Tangente an F aus
bildet, die Steigung der Tangente an F aus 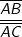 . Nun sind die Strecken
. Nun sind die Strecken 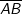 und
und 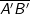 sowie
sowie 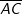 und
und 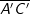 gleich lang. Mit anderen Worten, die Steigung der Tangente an F-1 ist gleich der reziproken Steigung der Tangente an F. Damit gilt:
gleich lang. Mit anderen Worten, die Steigung der Tangente an F-1 ist gleich der reziproken Steigung der Tangente an F. Damit gilt: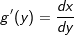 ist
ist 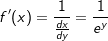 .
.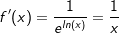 .
.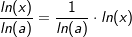 . Da wir nun aber die Ableitung von ln(x) kennen, leiten wir daraus die Ableitung von loga(x) ab mit:
. Da wir nun aber die Ableitung von ln(x) kennen, leiten wir daraus die Ableitung von loga(x) ab mit: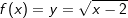 ist f-1(x)=x2+2 wobei f-1(x) auch als g(y)=y2+2 geschrieben werden kann. Nun gilt genau wie bei der Logarithmusfunktion
ist f-1(x)=x2+2 wobei f-1(x) auch als g(y)=y2+2 geschrieben werden kann. Nun gilt genau wie bei der Logarithmusfunktion 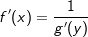 und
und 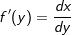 bzw.
bzw. 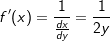 .
.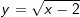 ist, ist
ist, ist 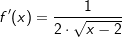 .
.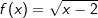 kann zu
kann zu 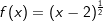 umgeschrieben werden und damit mit der uns bereits bekannten Potenzregel abgeleitet werden zu
umgeschrieben werden und damit mit der uns bereits bekannten Potenzregel abgeleitet werden zu 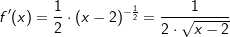 .
.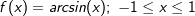 . Ihre Umkehrfunktion lautet f-1(x)=sin(x) bzw. g(y)=sin(y).
. Ihre Umkehrfunktion lautet f-1(x)=sin(x) bzw. g(y)=sin(y). 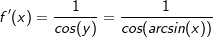 . Für den relevanten Wertebereich gilt jedoch
. Für den relevanten Wertebereich gilt jedoch 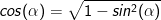 . Wir können den Nenner der Ableitung somit umschreiben:
. Wir können den Nenner der Ableitung somit umschreiben: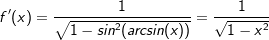 , womit wir die endgültige Ableitung von arcsin(x) erhalten haben.
, womit wir die endgültige Ableitung von arcsin(x) erhalten haben.