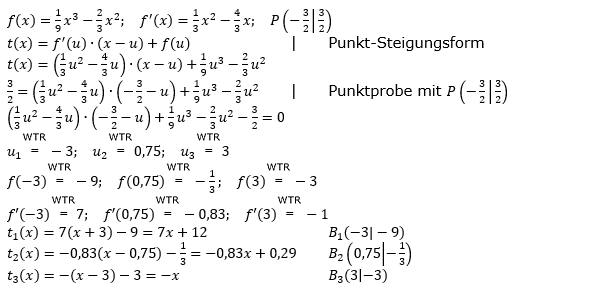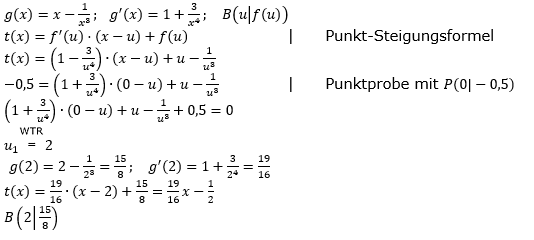 |
Ableitungen Tangente und Normale - Level 3 - Expert - Blatt 4 |
| Dokument mit 9 Aufgaben |
Aufgabe A1
Gegeben ist die Funktion f mit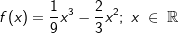 , ihr Schaubild sei K.Vom Punkt 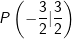 aus sollen Tangenten an K gelegt werden.Bestimme die Gleichungen der Tangenten und die dazugehörigen Berührpunkte. |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2
Gegeben ist die Funktion f mit 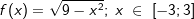 .Eine Tangente an den Graphen soll durch den Punkt P(5|0) gehen.
|
| Eine Frage stellen... |
Aufgabe A3
Gegeben ist eine Funktion f durch 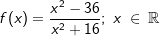 . Ihr Schaubild sei K. |
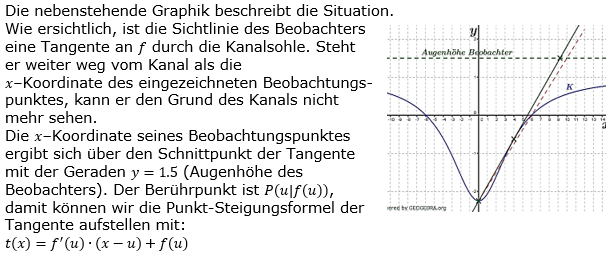
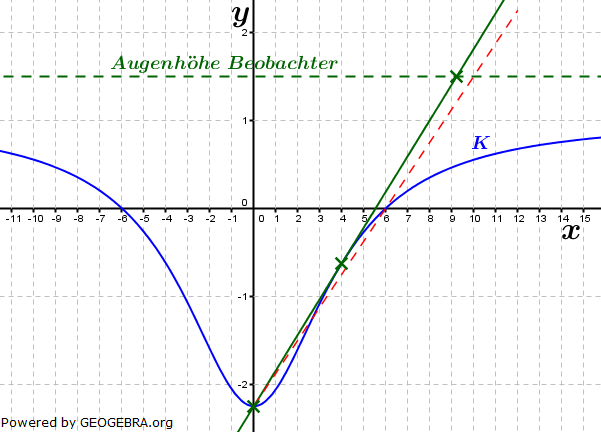
| Nun stellt K für -6≤x≤6 den Querschnitt eines 500 m langen Kanals dar (x in Meter, f(x) in Meter). Die sich anschließende Landfläche liegt auf der Höhe y=0. Der Pegelstand wird in Bezug auf den tiefsten Punkt des Kanals gemessen und beträgt maximal 2,25 m. |
| An Land steht eine Person. In welcher Entfernung vom Kanalrand darf sie höchstens stehen, damit sie bei leerem Kanal die tiefste Stelle des Kanals sehen kann (Augenhöhe 1,50 m)? |
| TIPP: Fertige zunächst eine Skizze der Situation. |
| Quelle: Teilaufgabe Abitur 2004 A1.1 Baden-Württemberg. |
| Eine Frage stellen... |
Aufgabe A4 (2 Teilaufgaben)
| Ein Tal in den Bergen wird nach Westen von einer steilen Felswand, nach Osten von einem flachen Höhenzug begrenzt. Der Querschnitt des Geländes wird beschrieben durch das Schaubild der Funktion f mit | ||||
| f(x)=-0,125x3+0,75x2-3,125 im Bereich -2,5≤x≤5, | ||||
| dabei weist die positive x-Achse nach Osten (1 LE entspricht 100 m). | ||||
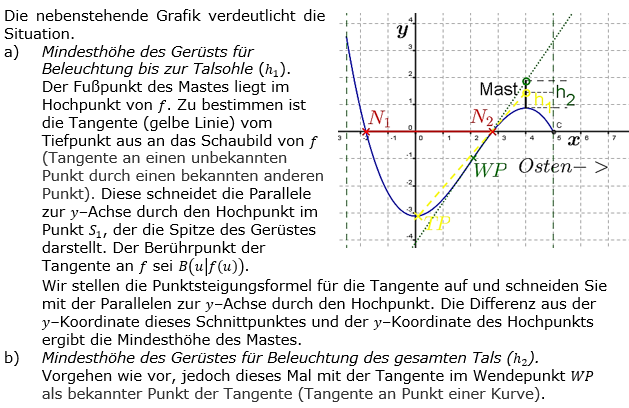
In der Talsohle befindet sich ein Dorf, das bereits nachmittags im Schatten liegt. Nach dem Vorbild des italienischen Ortes Yiganella soll auf dem höchsten Punkt des Höhenzugs östlich des Dorfes ein Gerüst mit einem drehbaren Spiegel zur Reflexion von Sonnenlicht aufgestellt werden. Auch hier wird der Querschnitt des Geländes durch das Schaubild der Funktion f beschrieben.
|
||||
| TIPP: Fertige zunächst eine Skizze der Situation. | ||||
| Quelle: Teilaufgabe Abitur 2008 A1.1 Baden-Württemberg. |
| Eine Frage stellen... |
Aufgabe A5
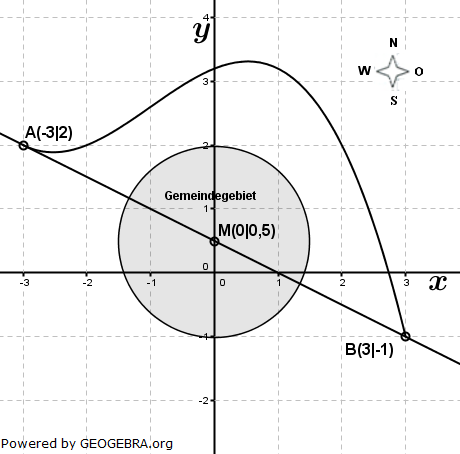
Die Abbildung zeigt den Verlauf einer Umgehungsstraße zur Entlastung der Ortsdurchfahrt  einer Gemeinde. Das Gemeindegebiet ist kreisförmig mit dem Mittelpunkt M und dem Radius r=1,5 km.Die Umgehungsstraße verläuft durch den Punkt A und B und wird beschrieben durch die Funktion f mit |
| f(x)=-0,1x3-0,3x2+0,4x+3,2. |
| Eine LE entspricht 1 km. |
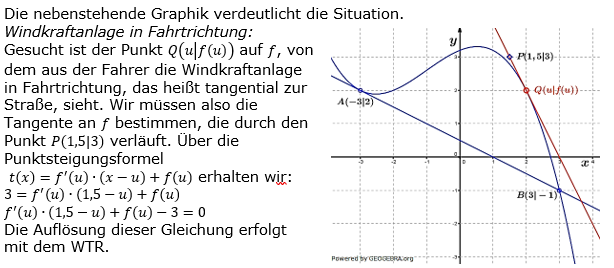
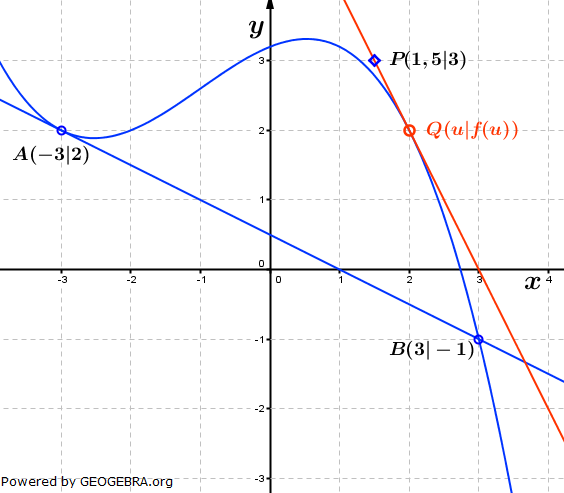
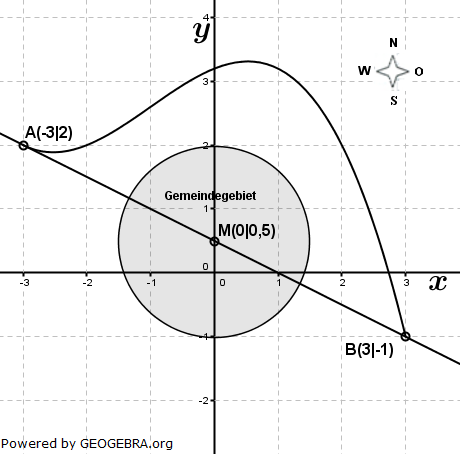 Im Punkt P(1,5|3) befindet sich eine Windkraftanlage. Ein Fahrzeug fährt von B aus auf die Umgehungsstraße. Von welchem Punkt der Umgehungsstraße aus sieht der Fahrer die Windkraftanlage genau in Fahrtrichtung vor sich? |
 |
| TIPP: Fertige zunächst eine Skizze der Situation. |
| Quelle: Teilaufgabe Abitur 2012 A1.1 Baden-Württemberg. |
| Eine Frage stellen... |
Aufgabe A6
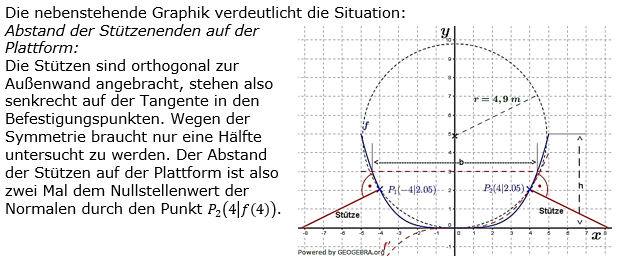
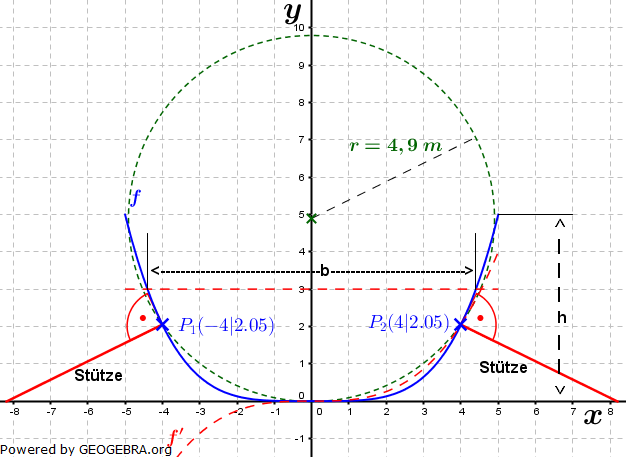
| Der Laderaum eines Lastkahns ist 50 m lang. Sein Querschnitt ist auf der gesamten Länge gleich und wird modellhaft beschrieben durch den Graphen der Funktion f mit |
 . |
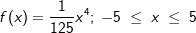| Zur Wartung steht der Lastkahn auf einer ebenen Plattform. Dort wird er stabilisiert durch gerade Stützen, die orthogonal zur Außenwand des Laderaums angebracht sind. Betrachtet werden zwei einander gegenüberliegende Stützen, deren Befestigungspunkte im Modell durch die Punkte P1 (-4|f(-4)) und P2 (4|f(4)), beschrieben werden. In welchem Abstand voneinander enden diese Stützen auf der Plattform? |
| TIPP: Fertige zunächst eine Skizze der Situation. |
| Quelle: Teilaufgabe Abitur 2015 A1.1 Baden-Württemberg. |
| Eine Frage stellen... |
Aufgabe A7
Die Funktion g ist gegeben durch  . |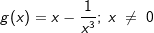
| Die Tangente an den Graphen von g im Punkt B verläuft durch P(0|-0,5). Bestimmen Sie die Koordinaten von B. |
| Quelle: Teilaufgabe Abitur 2017 A1.2 Baden-Württemberg. |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Tangente und Normale - Level 3 - Expert - Aufgabenblatt 4 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
