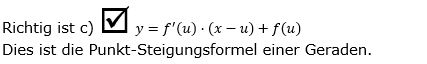 |
Ableitungen Tangente und Normale - Level 1 - Grundlagen - Blatt 4 |
| Dokument mit 11 Aufgaben |
Aufgabe A1
| Ist die Funktion f differenzierbar und P(u|f(u)) ein Punkt des Graphen von f, so lautet die Gleichung der Tangente an den Graphen von f in P: | |||
| Richtig ist: | |||
| a) | y=f'(u)⋅x-u+f(u) | a) |  |
| b) | y=f(u)⋅(x-u)+f'(u) | b) | |
| c) | y=f'(u)⋅(x-u)+f(u) | c) | |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (3 Teilaufgaben)
| Entscheide, ob die folgenden Aussagen über Tangenten wahr oder falsch sind: | |||||
| Wahr | Falsch | ||||
| a) | Die Gleichung einer Tangente kann man immer in der Form y=m⋅x schreiben. | a) | |
|
|
| b) | Jede Tangente schneidet die x-Achse. | b) | |
|
|
| c) | Die Tangente in einem Punkt (x0|f(x0)) schneidet nie den Graphen der Funktion f. | c) | |
|
|
| Eine Frage stellen... |
Aufgabe A3 (3 Teilaufgaben)
| Geben Sie die Gleichung der Tangente an den Graphen von f an der Stelle x1 an. | |||||
| Tangenten: | |||||
| a) | f(x)=0,5x2 mit x1=1 | a) y | = ____⋅x+____ | ||
| b) | g(x)=sin(x) mit x1=π | b) y | = ____⋅x+____ | ||
| c) | h(x)=e2x mit x1=0 | c) y | = ____⋅x+____ | ||
| Eine Frage stellen... |
Aufgabe A4 (2 Teilaufgaben)
| Gegeben ist die Funktion f mit f(x)=4-0,5x2. | |||
| a) | Bestimme die Gleichung der Tangente an der Stelle x=1,5. | a) | y = ____⋅x+____ |
| b) | Bestimme den Schnittpunkt S der Tangenten mit der x-Achse (auf drei Dezimalstellen gerundet). | b) | S ( | ) |
| Eine Frage stellen... |
Aufgabe A5
| Die Gleichung der Tangenten an den Graphen einer Funktion f im Punkt P lautet y=3x+4. Entscheide, welches die zugehörige Normalengleichung im Punkt P sein könnte. |
|
y = -3x + 4 |
|
 |
|
|
 |
| Eine Frage stellen... |
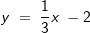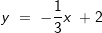Aufgabe A6
 Das Schaubild zeigt für x≤2 den Graphen der Funktion f mitf(x)=0,5x-2+1. Welche Gleichung gehört dann zur Geraden g? |
|
g(x) = -2,86x + 7,3 |
|
g(x) = -2,86x + 2,54 | |
|
g(x) = -0,693x + 3,39 |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Ableitungen Tangente und Normale - Level 1 - Grundlagen - Blatt 4 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
