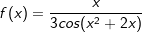|
|
Ableitungen - trigonometrische Funktionen |


| Titel Aufgabenblatt | Level / Blattnr. |
| Ableitung trigonometrische Funktionen Aufgabenblatt Level 1/Blatt 1 25 Aufgaben im Blatt |
| Ableitung trigonometrische Funktionen Aufgabenblatt Level 2/Blatt 1 30 Aufgaben im Blatt |
| Ableitung trigonometrische Funktionen Aufgabenblatt Level 2/Blatt 2 24 Aufgaben im Blatt |
| Ableitung trigonometrische Funktionen Aufgabenblatt Level 3/Blatt 1 15 Aufgaben im Blatt |
| Ableitung trigonometrische Funktionen Aufgabenblatt Level 3/Blatt 2 14 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

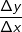 für Δx⟶0.
für Δx⟶0.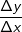 entsprechend der
entsprechend der  -Methode, wie wir dies in den anderen Kapiteln auch kennengelernt haben.
-Methode, wie wir dies in den anderen Kapiteln auch kennengelernt haben.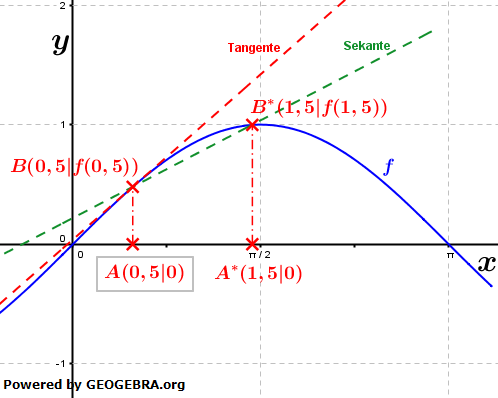 Zunächst die Steigung der Sekante durch die Punkte B und B'.
Zunächst die Steigung der Sekante durch die Punkte B und B'. 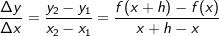
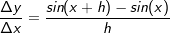
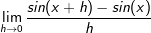 müssen wir zunächst noch ein paar Umformungen vornehmen. Über das Additionstheorem
müssen wir zunächst noch ein paar Umformungen vornehmen. Über das Additionstheorem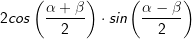 erhalten wir
erhalten wir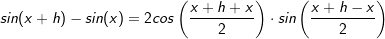
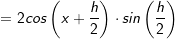
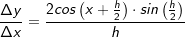 . Wir erweitern diesen Bruch mit
. Wir erweitern diesen Bruch mit  und erhalten:
und erhalten: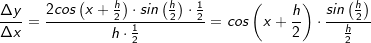
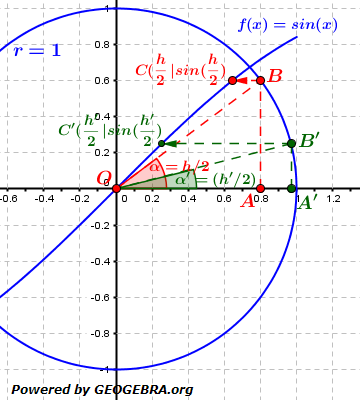 Es erfolgt nun der Nachweis, dass
Es erfolgt nun der Nachweis, dass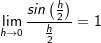 ist. Hierzu betrachten wir uns die Situation am Einheitskreis.
ist. Hierzu betrachten wir uns die Situation am Einheitskreis.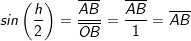 . Dieser Wert liegt auf der Sinuskurve im Punkt
. Dieser Wert liegt auf der Sinuskurve im Punkt 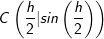 .
.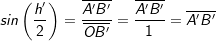 . Dieser Wert liegt auf der Sinuskurve im Punkt
. Dieser Wert liegt auf der Sinuskurve im Punkt 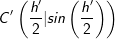 .
.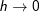 wird
wird 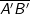 immer kleiner und damit wandert
immer kleiner und damit wandert 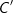 gegen den Ursprung.
gegen den Ursprung.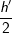 immer kleiner wird, streben sowohl
immer kleiner wird, streben sowohl 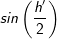 demselben Wert entgegen, sodass der Quotient aus
demselben Wert entgegen, sodass der Quotient aus 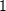 strebt.
strebt.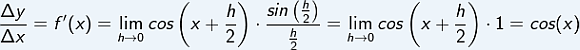
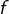 mit
mit 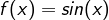 hat die Funktionsgleichung
hat die Funktionsgleichung 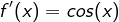
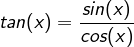
 mit
mit 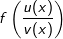 ist
ist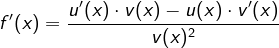
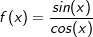 gilt:
gilt: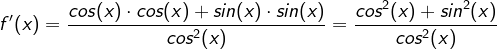 .
.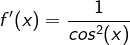
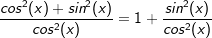 gilt aber auch:
gilt aber auch: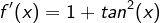 .
.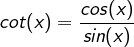
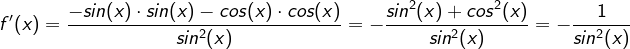 ,
,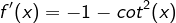 .
.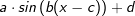 ,
, 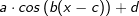 bzw.
bzw. 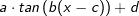 und auch keine mit anderen Funktionstypen zusammengesetzte Funktionen wie etwa
und auch keine mit anderen Funktionstypen zusammengesetzte Funktionen wie etwa 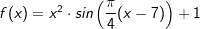 oder gar
oder gar 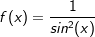 ableiten. Für solche Ableitungen benötigen wir zusätzliche Regeln wie etwa die Produkt- und Quotientenregel sowie die Kettenregel.
ableiten. Für solche Ableitungen benötigen wir zusätzliche Regeln wie etwa die Produkt- und Quotientenregel sowie die Kettenregel. 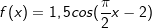
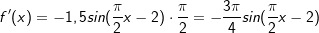

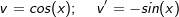

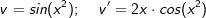
 mit
mit