|
Ableitungen Tangente und Normale - Level 3 - Expert - Blatt 2 |
| Dokument mit 16 Aufgaben |
Aufgabe A1 (5 Teilaufgaben)
Gegeben ist die Funktion f mit f(x)=x3-6.
|
| |
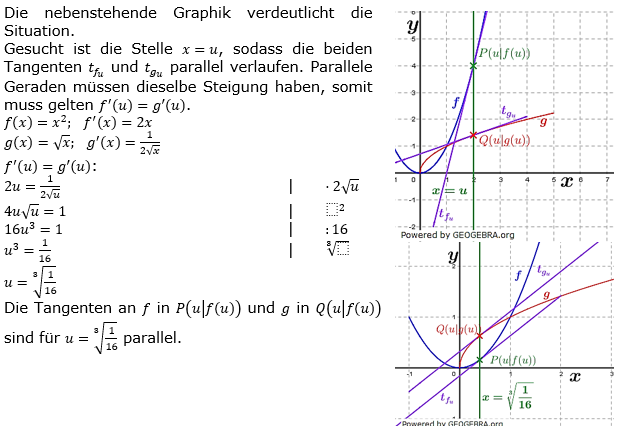
Lösung A1-d)
| In nebenstehender Grafik sehen wir zunächst die Ausgangssituation. Es gibt zwei Tangenten an den Graphen der Kurve, einmal im Punkt P und zusätzlich eine Tangente vom Punkt P aus. |
|
| Du kannst die Animation starten, indem du auf das Beachte, wie durch den Punkt P stets zwei Tangenten verlaufen, nämlich einmal die Tangente an den Grpahen im Punkt P und zum zweiten die Tangente vom Punkt P aus an den Graphen mit dem Berührpunkt Q. Wenn du die Animation anhältst und den Schieberegler u mit der Maus auf den Wert 0 einstellst, erkennst du, dass die beiden Tangenten zu einer Tangente zusammenfallen. Facit: Miriana hat zwar recht mit einer Ausnahme, dass die beiden Tangenten zu einer Tangente im Wendepunkt des Graphen der Funktion zusammenfallen. |
|
| |
Aufgabe A2 (2 Teilaufgaben)
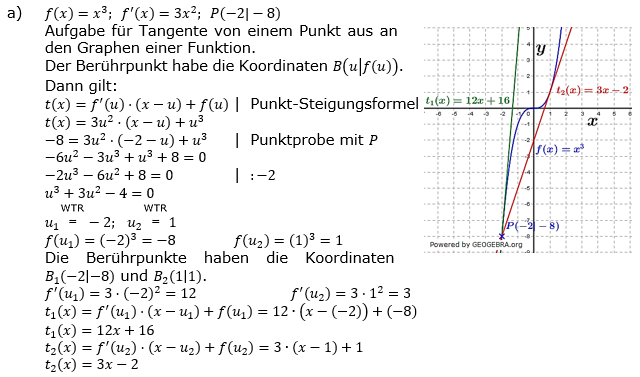
| a) | Bestimme die Gleichung der Tangente t an den Graphen von f mit f(x)=x3, die durch den Punkt P(-2│-8) verläuft. Gib auch den Berührpunkt an. |
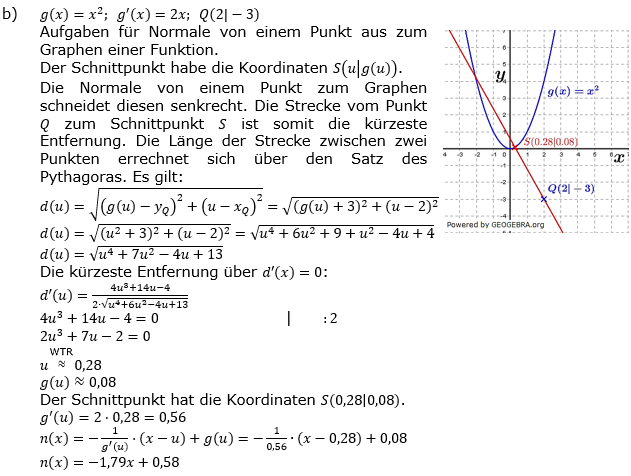
| b) | Bestimme die Gleichung der Normalen n zum Graphen von g mit g(x)=x2, die durch den Punkt Q(2│-3) verläuft. Gib auch den Schnittpunkt von n mit g an. |
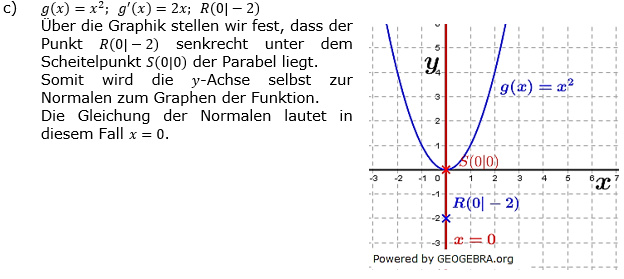
| c) | Bestimme die Gleichung der Normalen n zum Graphen wie unter Teilaufgaben b), die jedoch durch den Punkt R(0│-2) verläuft. (Mache zunächst eine Skizze). |
| |
Aufgabe A3
| Gegeben ist die Funktion f mit f(x)=2x2+4. Bestimme die Punkte des Graphen von f, dessen Tangenten durch den Punkt P(1|-2) verlaufen. |
| |
Aufgabe A4 (3 Teilaufgaben)
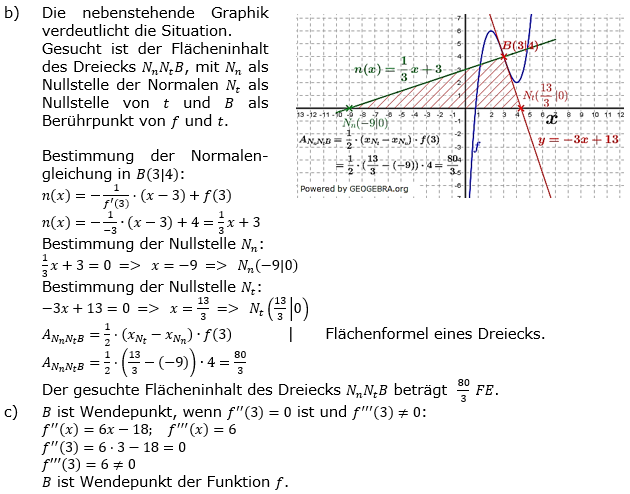
Die Gerade t mit der Gleichung y=-3x+13 ist Tangente an den Graphen der Funktion f mit f(x)=x3-9x2+24x-14.
|
| |
Aufgabe A5
Gegeben sind die Funktionen f(x)=x2 sowie 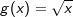 . .Die senkrechte Gerade g mit der Gleichung x=u schneidet das Schaubild von f im Punkt P und das Schaubild von g im Punkt Q. Bestimme u so, dass die Tangenten in P und Q parallel sind. |
| |
Aufgabe A6
Zeige, dass sich die Schaubilder von f(x)=x2-2x+1 und 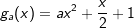 im Punkt S(0|1) für jeden Wert von a sich rechtwinklig schneiden. im Punkt S(0|1) für jeden Wert von a sich rechtwinklig schneiden. |
| |
Aufgabe A7
| An den Parabelbogen der Funktion f mit f(x)=-0,4(x-2)2-1,5 soll vom Punkt P(0|5) ausgehend eine Tangente so gelegt werden, dass ihr Steigung einen negativen Wert annimmt. Bestimme die Gleichung der Tangente und die Koordinaten des Berührpunktes B. |
| |
Aufgabe A8 (2 Teilaufgaben)
Gegeben ist die Funktion fa mit f(x)=a∙(x3-4x+2); a∈R, a≠0.
|
| |
| Du befindest dich hier: |
| Ableitungen Tangenete und Normale - Level 3 - Expert - Blatt 2 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

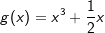 und h mit h(x)=(x+2)⋅x⋅(4-x).
und h mit h(x)=(x+2)⋅x⋅(4-x).