 |
|
WIKI zu den Zehnerpotenzen |
|


- Zehnerpotenzen Einleitung
- Videos zu den Zehnerpotenzen
- Regeln und Beispiele
- Zusammenfassung der Regeln
- Video 'Faszination Zehnerpotenzen'
1. Zehnerpotenzen Einleitung
| Am 17. Februar 2013 meldet AFP | dpa: Höchstleistungen Deutschland hat den schnellsten Supercomputer in Europa  Europas schnellster Super-computer Juqueen schafft nach Angaben des Forschungs-zentrums Jülich 5,9 Petaflopas (Rechenschritte pro Sekunde). Die von IBM gebaute Anlage sei rund 100.000 Mal schneller als ein moderner PC. Europas schnellster Super-computer Juqueen schafft nach Angaben des Forschungs-zentrums Jülich 5,9 Petaflopas (Rechenschritte pro Sekunde). Die von IBM gebaute Anlage sei rund 100.000 Mal schneller als ein moderner PC.Das neue System wird unter anderem von Jülicher Hirnforschern genutzt, um die Hirnstrukturen zu simulieren... (Quelle: Kernforschungszentrum Jülich) ____________________________ In Technik und Wissenschaft treffen wir immer entweder sehr große Zahlen oder aber sehr kleine Zahlen an. So finden wir z. B. in o.a. Artikel die Angabe "5,9 Petaflops". Was verbirgt sich denn hinter dieser Bezeichnung? Nun, „Peta“ ist eine Abkürzung für die Zehnerpotenz 1015. Die Bezeichnung 5,9 Petaflops entspricht also der Zahl 5,9⋅1015 Flops (Flops steht für Rechenschritte pro Sekunde). Wollten wir dieser Zahl ausschreiben, so müssten wir die Zahl 5.900.000.000.000.000 schreiben, was ausgesprochen „fünf Billiarden und 900 Billionen" ist. Wir können also Zahlen mit sehr vielen Nullen kürzer aufschreiben, indem wir uns der Zehnerpotenzen bedienen. |
2. Videos zu den Zehnerpotenzen
| Um zu lernen, wie du mit Zehnerpotenzen rechnen musst, kannst du dir die nachfolgenden Videos ansehen, oder aber du liest dir die verbalen Beschreibungen im Einzelnen durch. |
3. Regeln und Beispiele
3.1. Sehr große Zahlen
| Die Zahl 5000000000 soll als Zehnerpotenz geschrieben werden. Unsere Zahl hat ja neun Nullen. Diese Anzahl von Nullen wird dann zum Exponenten (zur Hochzahl) der Basis 10, also 109. Damit ist: 5000000000=5⋅109. |
| Nun gibt es aber auch sehr kleine Zahlen wie z. B. die Zahl 0,000000005, die „fünf Milliardstel“ auszusprechen wäre. |
3.2. Sehr kleine Zahlen
| Die Zahl 0,000000005 soll als Zehnerpotenz geschrieben werden. Diese Zahl hat insgesamt neun Nachkommastellen. Die Anzahl der Nachkommastellen wird zum Exponenten (zur Hochzahl) der Basis 10, allerdings mit negativem Vorzeichen, also 10-9. Damit ist: 0,000000005=5⋅10-9. |
3.3. Wissenschaftliche Schreibweise
Die allgemeine Syntax einer Zehnerpotenz lautet: (Hinweis: 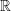 ist die Menge der reellen Zahlen, ist die Menge der reellen Zahlen, 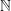 ist die Menge der natürlichen Zahlen, also aller negativen und positiven Zahlen einschließlich der Null). ist die Menge der natürlichen Zahlen, also aller negativen und positiven Zahlen einschließlich der Null).Steht 10n alleine, so ist a=1 und ist gleichbedeutend mit 1⋅10n. Für n=0 gilt: 100=1 Für n>0 gilt: Die Kommastelle von a wird um n Stellen nach rechts verschoben. Für n<0 gilt: Die Kommastelle von a wird um n Stellen nach links verschoben. |
3.4. Umwandlung in Dezimalzahlen
| Dezimalzahlen mit der Zehnerpotenz Null: | |||||||||||
|
| Dezimalzahlen mit der Zehnerpotenz größer Null: Die Kommastelle (auch eine eventuell gedachte Kommastelle) der Vorzahl der Zehnerpotenz wird umso viele Stellen nach rechts verschoben, wie die Hochzahl angibt. |
|||||||||||
|
| Dezimalzahlen mit der Zehnerpotenz kleiner Null: Die Kommastelle (auch eine eventuell gedachte Kommastelle) der Vorzahl der Zehnerpotenz wird umso viele Stellen nach links verschoben, wie die Hochzahl angibt. |
|||||||||||
|
3.5. Umwandlung von Dezimalzahlen beliebig
| In der Umkehrung können wir aber auch Dezimalzahlen in Zehnerpotenzen umwandeln. Sei a≠0 eine positive reelle Zahl, so gilt: Für a>1 und a verkleinern: Wir verschieben das Komma von a nach links und schreiben a⋅10n, wobei n die Anzahl der verschobenen Kommastellen ist. Für a>1 und a vergrößern: Wir verschieben das Komma von a nach rechts und schreiben a⋅10n, wobei n die Anzahl der verschobenen Kommastellen ist. Für a<1 und a verkleinern: Wir verschieben das Komma von a nach links und schreiben a⋅10-n, wobei n die Anzahl der verschobenen Kommastellen ist. Für a<1 und a vergrößern: Wir verschieben das Komma von a nach rechts und schreiben a⋅10-n, wobei n die Anzahl der verschobenen Kommastellen ist. Vergrößern der Vorzahl a: Die Vorzahl a wird vergrößert, indem man das Komma nach rechts schiebt und die Anzahl der verschobenen Kommastellen als negative Hochzahl von 10 schreibt:
Die Vorzahl a wird verkleinert, indem man das Komma nach links schiebt und die Anzahl der verschobenen Kommastellen als positive Hochzahl von 10 schreibt.
|
3.6. Umwandlung von Zahlen in die wissenschaftliche Schreibweise
| Wir wir in zuvor nun gesehen haben, lässt sich eine reelle Zahl auf vielfältige Weise in eine 10–er Potenz umwandeln. Da dies zu den unterschiedlichsten Darstellungen führt, hat man sich auf eine einheitliche Darstellung geeinigt - die sogenannte „Wissenschaftliche Schreibweise“. Die wissenschaftliche Schreibweise besagt, dass die dargestellte reelle Zahl immer eine und nur eine Ziffer ungleich Null vor dem Komma und alle anderen Ziffern nach dem Komma stehen müssen. Somit gilt für diese Darstellung:  |
||||||||||||||||||||
Umwandlung von Dezimalzahlen größer als Null:
|
||||||||||||||||||||
Umwandlung von Dezimalzahlen kleiner als Null:
|
||||||||||||||||||||
Umwandlung Zehnerpotenzen allgemein in Zehnerpotenzen wissenschaftlich:
|
3.7. Addition / Subtraktion
3.8. Multiplikation / Division
| Zehnerpotenzen lassen sich nach den Regeln der Multiplikation bzw. Division umformen, wobei für die Zehnerpotenzen die Regeln des 1. und 2. Potenzgesetzes zu beachten sind. Es gilt: 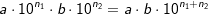 bzw. bzw.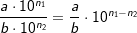
3.8.1. Beispiele 16 - 27
|
|||||||||||||||||||||||||||||||||||||||
Auch hier gilt, dass bei Anforderung des Ergebnisses in wissenschaftlicher Schreibweise dieses nach Ausführung der Berechnung gegebenenfalls in die wissenschaftliche Schreibweise umgewandelt werden muss.
3.8.2. Beispiele 28 - 33
|
|||||||||||||||||||||||||||||||||||||||
3.9. Vorsätze von Maßeinheiten
| Im Alltag, in der Wissenschaft und Technik sowie in der Physik treffen wir häufig Vorsätze zu Maßeinheiten an, so z. B. den Meter, den Zentimeter, den Kilometer, den Mikrometer usw., oder das Gramm, das Kilogramm, das Milligramm usw. In der Physik finden wir Maßeinheiten wie z. B. Joule, Kilojoule, Petajoule usw. Wiederstände werden in Ohm, Kiloohm usw., Kapazitäten in Farad, Nanofarad, Picofarad usw. angegeben. Hinter diesen Vorsätzen zu den Maßeinheiten verbirgt sich nichts Anderes als bestimmte Zehnerpotenzen. Die nachfolgende Tabelle gibt Aufschluss darüber, welcher Vorsatz zu welcher Zehnerpotenz gehört. 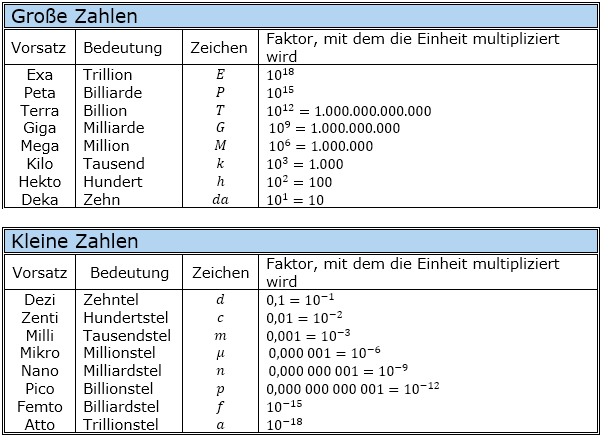 |
4. Zusammenfassung der Regeln
Merksatz
| Zehnerpotenzen | |||||||||||
| Allgemeine Syntax: | |||||||||||
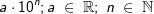 |
|||||||||||
|
|||||||||||
| Wissenschaftliche Schreibweise: | |||||||||||
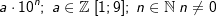 |
|||||||||||
| Addition / Subtraktion: | |||||||||||
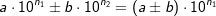 falls n1 = n2. falls n1 = n2. |
|||||||||||
|
|||||||||||
| Multiplikation / Division: | |||||||||||
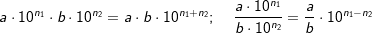 |
|||||||||||
| Titel Aufgabenblatt | Level / Blattnr. |
Zehnerpotenzen Aufgabenblatt Level 1 / Blatt 1  63 Aufgaben im Blatt |
Zehnerpotenzen Aufgabenblatt Level 1 / Blatt 2 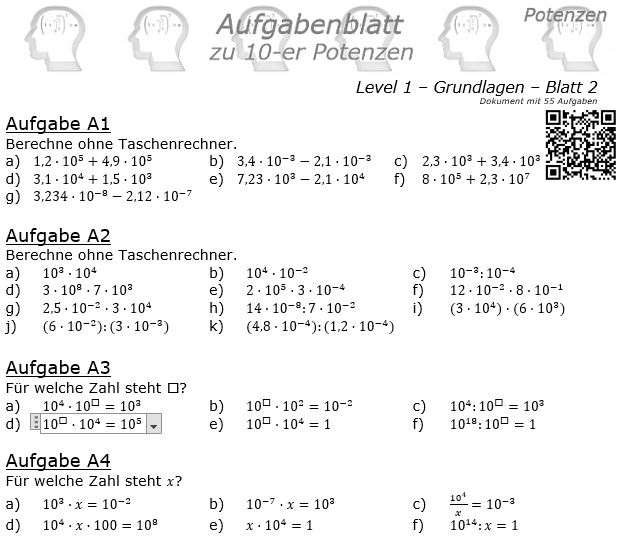 55 Aufgaben im Blatt |
Zehnerpotenzen Aufgabenblatt Level 2 / Blatt 1  64 Aufgaben im Blatt |
Zehnerpotenzen Aufgabenblatt Level 2 / Blatt 2  29 Aufgaben im Blatt |
Zehnerpotenzen Aufgabenblatt Level 3 / Blatt 1  14 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021

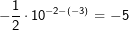
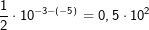
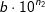 so umgewandelt werden, dass n2=n1 ist, bzw.
so umgewandelt werden, dass n2=n1 ist, bzw. 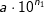 so umgewandelt werden, dass n1=n2 ist.
so umgewandelt werden, dass n1=n2 ist.

