 |
2017 - 2020 Abituraufgaben BG Matrizen | Prozesse (ohne Hilfsmittel) |
| Dokument mit 12 Aufgaben |
Aufgabe A3.1/2021 (3 Teilaufgaben)
| 3.1.1 | Gegeben sind die Matrizen A und B. Die Matrix A hat 2 Zeilen und 3 Spalten, d.h. A hat das Format 2×3. B hat das Format 3×2. Geben Sie an, welche der folgenden beiden Berechnungen möglich ist: |
||
| (1) | 3⋅A+2⋅B | ||
| (2) | A⋅B | ||
| Bestimmen Sie das Format der Ergebnismatrix. | (2P) | ||
| 3.1.2 | Für jede Matrix 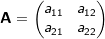 bezeichnet bezeichnet 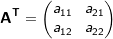 die transponierte Matrix von A. Eine Matrix A heißt orthogonal, falls die transponierte Matrix von A. Eine Matrix A heißt orthogonal, falls 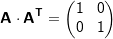 . . |
||
| 3.1.2.1 | Prüfen Sie, ob die Matrix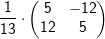 orthogonal ist. orthogonal ist. |
(2P) | |
| 3.1.2.2 | Zeigen Sie, dass 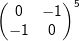 orthogonal ist. orthogonal ist. |
(3P) | |
| |
Aufgabe A3.2/2021 (3 Teilaufgaben)
| 3.2.1 | Berechnen Sie den Lösungsvektor des linearen Gleichungssystems, das durch die folgende erweiterte Koeffizientenmatrix gegeben ist: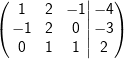 |
(3P) | |
| 3.2.2 | Gegeben sind die Matrizen 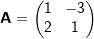 und und 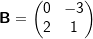 |
||
| 3.2.2.1 | Zeigen Sie, dass die Matrizenmultiplikation von A und B nicht kommutativ ist, das heißt A∙B≠B∙A. | (2P) | |
| 3.2.2.2 | Durch Abänderung genau eines Koeffizienten der Matrix B lässt sich eine Matrix 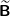 erzeugen, die die folgenden beiden Eigenschaften hat: erzeugen, die die folgenden beiden Eigenschaften hat: |
||
| (1) | 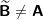 |
||
| (2) | Die Matrizenmultiplikation von A und 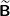 ist kommutativ. ist kommutativ. |
||
| Geben Sie eine mögliche Matrix an. | (2P) | ||
| |
Aufgabe A3.1/2022 (3 Teilaufgaben)
| 3 | Die Matrix S ist gegeben durch | ||
S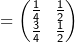 |
|||
| E bezeichnet die Einheitsmatrix vom Format 2 x 2. | |||
| 3.1 | Im Folgenden ist 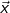 mit mit 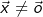 ein Vektor, sodass S ein Vektor, sodass S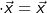 gilt. gilt. |
||
| 3.1.1 | Vereinfachen Sie den Ausdruck (S4+S3+S2+S-E)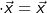 so weit wie möglich. so weit wie möglich. |
(2P) | |
| 3.1.2 | Bestimmen Sie einen solchen Vektor 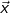 |
(2P) | |
| 3.2 | Eine quadratische Matrix heißt stochastische Matrix, falls alle ihre Elemente nicht negativ sind und für jede Spalte die Summe der Elemente den Wert 1 hat. Somit ist S eine stochastische Matrix. Beurteilen Sie, ob die folgende Aussage wahr oder falsch ist: „Ist M eine beliebige stochastische Matrix vom Format 2 x 2, so ist S∙M eine stochastische Matrix.“ |
||
| |
Aufgabe A3.2/2022 (3 Teilaufgaben)
| 3 | Gegeben sind die Matrizen | ||
A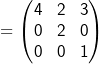 und B und B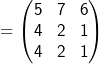 . . |
|||
| 3.1 | Berechnen Sie die Inverse von A. | (2P) | |
| 3.2 | Begründen Sie, dass die Gleichung B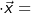 A A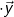 für jede Wahl von für jede Wahl von 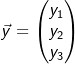 keine eindeutige Lösung 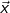 besitzt. besitzt. |
(2P) | |
| 3.3 | Untersuchen Sie, ob für die Matrizengleichung A2-B2=(A+B)(A-B) gilt, ohne eine der vier Matrizen A2, B2 ,A+B und A-B dabei zu berechnen. |
3P | |
| |
| Du befindest dich hier: |
| 2021 - heute Abituraufgaben BG Matrizen | Prozesse (ohne Hilfsmittel) |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 20. August 2022 20. August 2022









