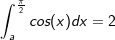|
2017 - 2020 Abituraufgaben BG Analysis (ohne Hilfsmittel) |
| Dokument mit 15 Aufgaben |
Aufgabe A1/2017 (6 Teilaufgaben)
| 1.1 | Geben Sie die Nullstellen von f mit 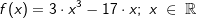 an. an. |
(2P) | ||
| 1.2 | Die Funktion erfüllt folgende Bedingungen: g'(3)=0 g''(3)=0 g'''(3)≠0 Welche Aussagen lassen sich damit über das Schaubild der Funktion g treffen? |
(2P) | ||
| 1.3 | Gegeben ist die Funktion h mit h(x)=e2x-4∙x; x ∈ R. | |||
| 1.3.1 | Bestimmen Sie den Punkt, an dem das Schaubild von h eine waagrechte Tangente hat. | (3P) | ||
| 1.3.2 | Ermitteln Sie die Stammfunktion von h, deren Schaubild durch den Punkt P(0|5) verläuft. | (3P) | ||
| 1.4 | Gegeben ist die Funktion p mit p(x)=cos(x); x ∈ R. | |||
| 1.4.1 | Es gilt: 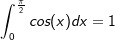 . Bestimmen Sie ohne Verwendung einer Stammfunktion zwei verschiedene Werte für a, sodass gilt: . Bestimmen Sie ohne Verwendung einer Stammfunktion zwei verschiedene Werte für a, sodass gilt:
|
(3P) | ||
| 1.4.2 | Beschreiben Sie, wie das Schaubild von q mit q(x)=-cos(x+2) aus dem Schaubild von p hervorgeht. | (2P) |
| |
Aufgabe A1/2018 (4 Teilaufgaben)
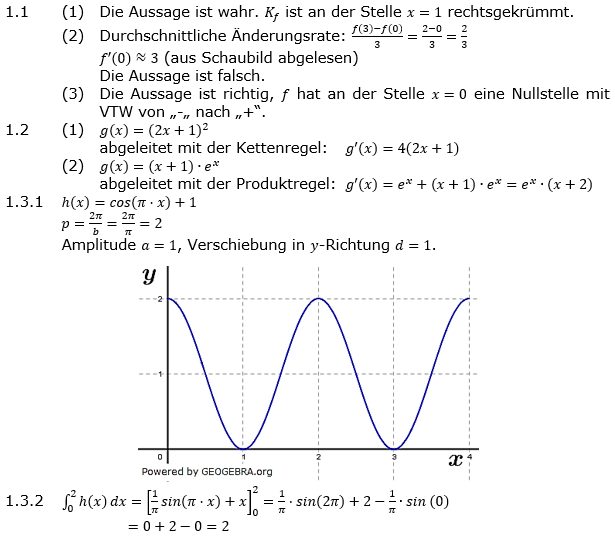
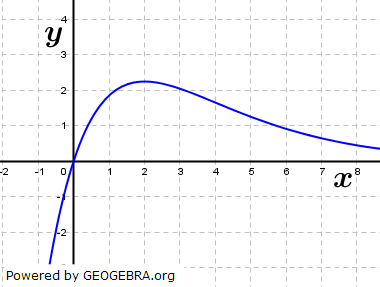
| 1.1 | Die Abbildung zeigt einen Ausschnitt des Schaubilds Kf einer Funktion f. | |||||||
 |
||||||||
Welche der folgenden Aussagen sind wahr bzw. falsch? Begründen Sie.
|
(6P) | |||||||
| 1.2 | Berechnen Sie die erste Ableitung g' für die jeweilige Funktion g.
|
(3P) | ||||||
| 1.3 | Gegeben ist die Funktion h mit 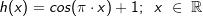 . . |
|||||||
| 1.3.1 | Skizzieren Sie das Schaubild von h für 0≤x≤4. | (3P) | ||||||
| 1.3.2 | Berechnen Sie : 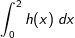 |
(3P) |
| |
Aufgabe A1/2019 (5 Teilaufgaben)
| 1.1 | Die folgende Abbildung zeigt einen Ausschnitt des Schaubilds einer Funktion f. | |
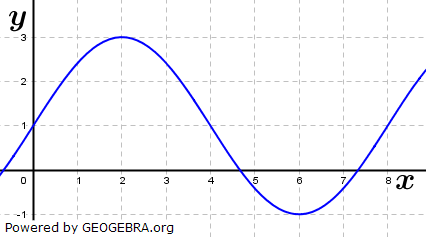 |
||
| 1.1.1 | Begründen Sie anhand der Abbildung, welche der folgenden Aussagen wahr oder falsch sind. | (6P) |
| (1) Es gilt: f'(1)>0 | ||
(2)  . . |
||
| (3) Für jede Stammfunktion F gilt F(4)=F(0). | ||
| 1.1.2 | Ermitteln Sie einen Funktionsterm einer trigonometrischen Funktion, die zu diesem Schaubild passt. | (3P) |
| 1.2 | Bilden Sie die erste Ableitung der Funktion 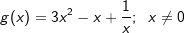 . . |
(2P) |
| 1.3 | Berechnen Sie den Wert des Integrals 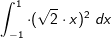 . . |
(2P) |
| 1.4 | Im Folgenden ist e die Eulersche Zahl und h die Funktion mit eh(x)=x für x > 0. Zeigen Sie mit Hilfe der Kettenregel: 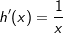 für x > 0. für x > 0. |
2P |
| |
Aufgabe A1/2020 (3 Teilaufgaben)
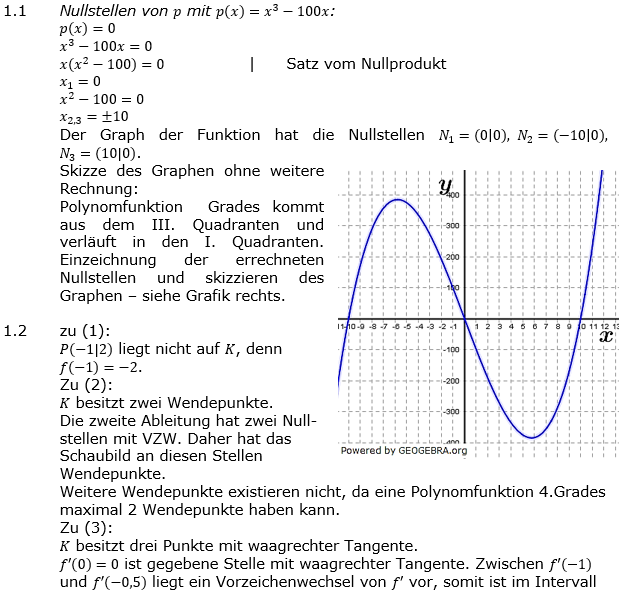
| 1.1 | Geben Sie die Nullstellen des Polynoms p mit 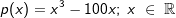 an. an.Erstellen Sie ohne weitere Rechnung eine Skizze des Schaubilds von p. |
(4P) | |||||||
| 1.2 | Die folgende Tabelle enthält Funktionswerte und Werte der ersten beiden Ableitungen einer Polynomfunktion h vom Grad 4. Das Schaubild von h ist K. | ||||||||
| x | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | ||
| f(x) | 2,375 | -2 | -1,625 | -1 | -1,625 | -2 | 2,375 | ||
| f'(x) | -18 | -2 | 2 | 0 | -2 | 2 | 18 | ||
| f''(x) | 48 | 18 | 0 | -6 | 0 | 18 | 48 | ||
| Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind und begründen Sie Ihre Entscheidungen ohne Funktionsterme zu berechnen. | |||||||||
| (1) | P(-1|2) liegt auf K. | ||||||||
| (2) | K besitzt zwei Wendepunkte. | ||||||||
| (3) | K besitzt drei Punkte mit waagrechter Tangente. | (6P) | |||||||
| 1.3 | Gegeben ist die Funktion f mit 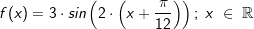 . . |
||||||||
| 1.3.1 | Geben Sie zwei benachbarte Wendepunkte des Schaubildes von f an. | (3P) | |||||||
| 1.3.2 | Ermitteln Sie einen Wert für b>10, für den gilt: 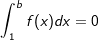 . . |
(2P) | |||||||
| |
| Du befindest dich hier: |
| 2017 - 2020 Abituraufgaben BG Analysis (ohne Hilfsmittel) |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 25. August 2021 25. August 2021