|
Abituraufgaben BG Prüfung 2019 Teil 1 (ohne Hilfsmittel) |
| Dokument mit 14 Aufgaben |
A1 Analysis (5 Teilaufgaben)
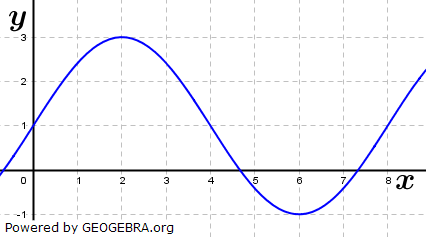
| 1.1 | Die folgende Abbildung zeigt einen Ausschnitt des Schaubilds einer Funktion f. | |
 |
||
| 1.1.1 | Begründen Sie anhand der Abbildung, welche der folgenden Aussagen wahr oder falsch sind. | (6P) |
| (1) Es gilt: f'(1)>0 | ||
(2)  . . |
||
| (3) Für jede Stammfunktion F gilt F(4)=F(0). | ||
| 1.1.2 | Ermitteln Sie einen Funktionsterm einer trigonometrischen Funktion, die zu diesem Schaubild passt. | (3P) |
| 1.2 | Bilden Sie die erste Ableitung der Funktion 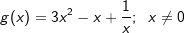 . . |
(2P) |
| 1.3 | Berechnen Sie den Wert des Integrals 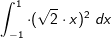 . . |
(2P) |
| 1.4 | Im Folgenden ist e die Eulersche Zahl und h die Funktion mit eh(x)=x für x > 0. Zeigen Sie mit Hilfe der Kettenregel: 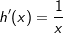 für x > 0. für x > 0. |
2P |
| |
A2 Stochastik (3 Teilaufgaben)
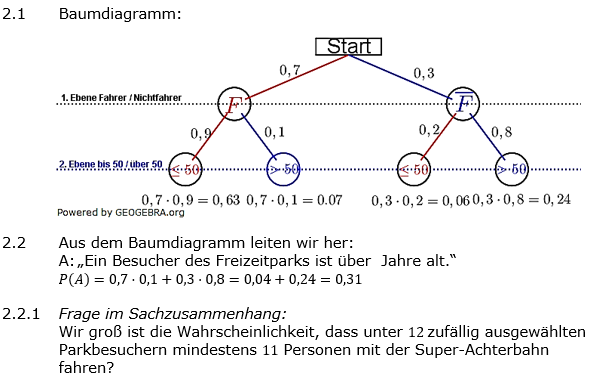
| 2. | Laut Statistik fahren 70 % aller Besucher eines Freizeitparks mit der extrem schnellen Super-Achterbahn. Von den Fahrern sind 10 % über 50 Jahre alt. Die Besucher, die nicht mit dieser Achterbahn fahren, sind zu 80 % über 50 Jahre alt. | |
| 2.1 | Stellen Sie den Sachverhalt in einem Baumdiagramm dar und tragen Sie die genannten Wahrscheinlichkeiten ein. | (2P) |
| 2.2 | Berechnen Sie die Wahrscheinlichkeit, dass ein Besucher des Freizeitparks über 50 Jahre alt ist. | (2P) |
| 2.2.1 | Geben Sie im Sachzusammenhang eine Fragestellung an, die mithilfe des Terms 0,712+12⋅0,3⋅0,711 beantwortet werden kann. | (2P) |
| |
| (Nur zu bearbeiten, wenn Wahlgebiet Vektorgeometrie im Unterricht behandelt.) |
| 3.1 | Bestimmen Sie die Lösungsmenge des folgenden linearen Gleichungssystems:
|
(2P) | |||||||||||||||
| 3.2 | Gegeben ist die Gerade mit 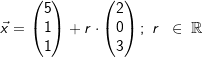 . . |
||||||||||||||||
| 3.2.1 | Begründen Sie, dass g parallel zur x1x3-Ebene ist. Geben Sie eine Gerade an, die parallel zur Geraden g ist und von dieser den Abstand 5 Längeneinheiten hat. |
(3P) | |||||||||||||||
| 3.2.2 | Berechnen Sie den Abstand, den der Punkt P(0|0|0) zu g hat. | (3P) |
| |
A3 Matrizen und Prozesse (3 Teilaufgaben)
| (Nur zu bearbeiten, wenn Wahlgebiet Matrizen/Prozesse im Unterricht behandelt.) |
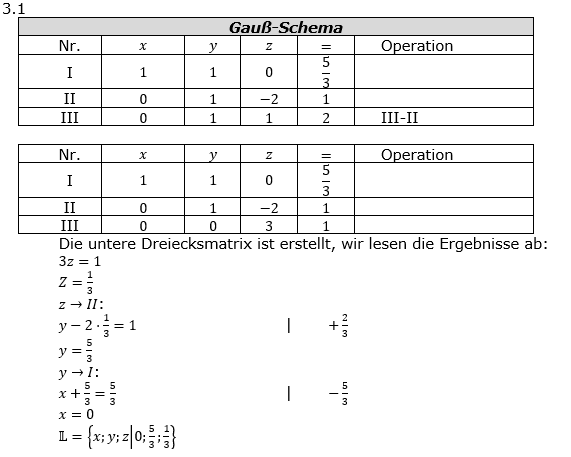
| 3.1 | Bestimmen Sie die Lösungsmenge des folgenden linearen Gleichungssystems: x + y = 5/3 y - 2z = 3 y + z = 2 |
(3P) |
| 3.2 | Im Folgenden ist E=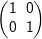 die Einheitsmatrix und A eine Matrix mit A⋅A=E. die Einheitsmatrix und A eine Matrix mit A⋅A=E. |
|
| 3.2.1 | Berechnen Sie die Werte für a und b, falls A=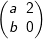 . . |
(3P) |
| 3.2.2 | Lösen Sie die folgende Matrizengleichung nach der 2×2-Matrix X auf: (A2-2X)A=2XA |
(3P) |
| |
| Du befindest dich hier: |
| Abituraufgaben BG Prüfung 2019 (ohne Hilfsmittel) |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 20. August 2022 20. August 2022