 |
Logarithmische Gleichungen - Level 2 - Fortgeschritten - Blatt 2 |
| Dokument mit 18 Aufgaben |
| In diesem Aufgabenblatt sind Aufgaben mit zwei Logarithmustermen. |
Aufgabe A1 (8 Teilaufgaben)
| Bestimme Definitions- und Lösungsmenge der folgenden logarithmischen Gleichungen. | ||
| a) | log2(x2+1)-log2(5)=log2(x)-1 | |
| b) | log2(3x-5)-log2(x-1)=log2(x)-1 | |
| c) | log(4x)+log(x)-1=log(5)+log(2) | |
| d) | log3(x)+log3(x+2)=log3(15) | |
| e) | log2(2x+6)=2+log2(x-2) | |
| f) | log7(x-2)-log7(x+4)+1=0 | |
| g) | log3(x-6)-log3(6)=log3(x+3)-2 |
|
| h) | log3(x-1)-log3(-2x)=2-log3(5x-2) | |
 Eine Frage stellen... |
Fehler melden...
Aufgabe A2 (10 Teilaufgaben)
| Ermittle die Definitions- und Lösungsmenge der folgenden logarithmischen Gleichungen mithilfe des Numerusvergleichs. | ||
| a) | log9(5-4x)=log9(1+4x) | |
| b) | log(x)-log(x+1)=-log(3) | |
| c) | log2(2x+6)-log2(2x-10)=log2(x-2) | |
| d) | log5(3x-2)-log5(3-2x)=0 | |
| e) | log(3x-5)-log(x+1)=log(13-4x) | |
| f) | log(x2-2x)-log(2x-3)=log(x-2) | |
| g) |  |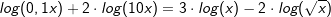
|
| h) | log(x)+log(2)=log(1+x2) | |
| i) | log(4x-5)-log(3-x)=log(2x+5)-log(5-x) | |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Logarithmische GleIchungen - Level 2 - Fortgeschritten - Blatt 2 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 24. September 2022 24. September 2022
