| 2 |
Eine ideale Münze zeigt nach jedem Wurf entweder Kopf oder Zahl an. |
|
| 2.1 |
Man wirft die Münze solange bis sie Zahl zeigt, jedoch höchstens dreimal. |
|
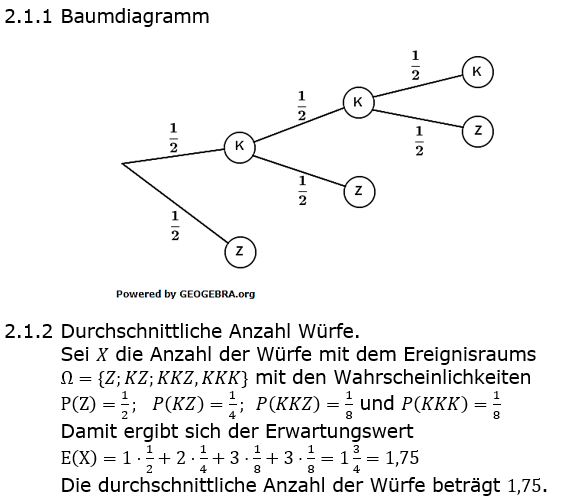
| 2.1.1 |
Zeichnen Sie ein Baumdiagramm, das dieses Zufallsexperiment vollständig beschreibt. |
(2P) |
| 2.1.2 |
Bestimmen Sie, wie oft man die Münze im Mittel wirft. |
(2P) |
| 2.2 |
Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind.
Begründen Sie: |
|
|
• |
Wird die Münze fünfmal hintereinander geworfen, so ist die Wahrscheinlichkeit für das Ereignis „genau einmal Zahl“ größer als  . . |
|
|
• |
Es gibt eine Anzahl von Würfen für die Folgendes gilt: Die Wahrscheinlichkeit für das Ereignis „genau dreimal Zahl“ ist gleich der Wahrscheinlichkeit für das Ereignis „genau zweimal Zahl“. |
(4P) |





 definierte Funktion f ist gegeben durch
definierte Funktion f ist gegeben durch 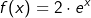 .
.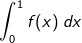 nach deren Größe in aufsteigender Reihenfolge.
nach deren Größe in aufsteigender Reihenfolge.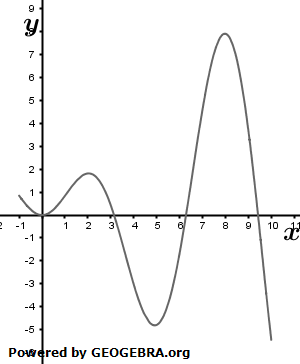
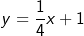 im Punkt (0|1) unter einem rechten Winkel
im Punkt (0|1) unter einem rechten Winkel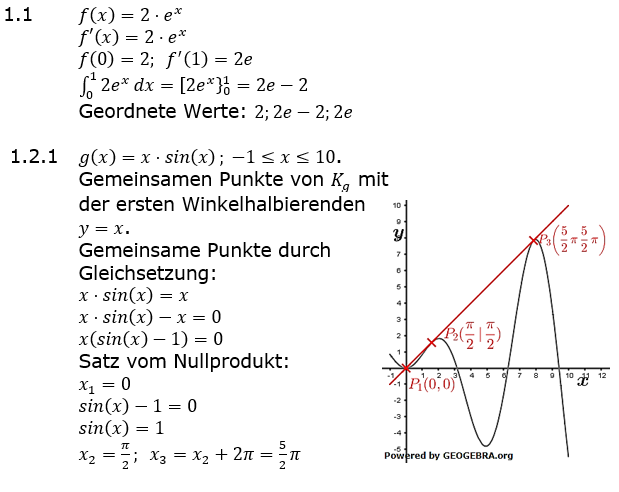


 .
.



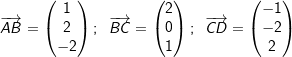 .
.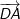 .
.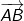 und
und 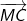 zueinander orthogonal sind.
zueinander orthogonal sind.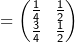
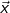 mit
mit 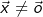 ein Vektor, sodass
ein Vektor, sodass 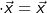 gilt.
gilt.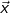


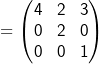 und
und 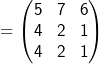 .
.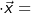
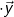 für jede Wahl von
für jede Wahl von 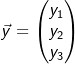
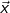 besitzt.
besitzt.



