|
Grafisch Differenzieren|Integrieren Pflichtteil allg. Gymnasium
|
Aufgaben der Prüfungsjahre 2004 - 2018 BW |
| Dokument mit 15 Aufgaben |
Lösungshinweis für alle Aufgaben
Aufgaben zum grafischen Differenzieren und Integrieren lösen wir mithilfe der sogenannten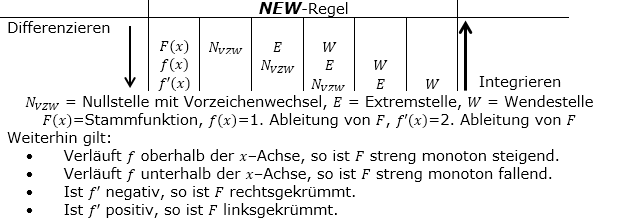 |
Aufgabe A4/04
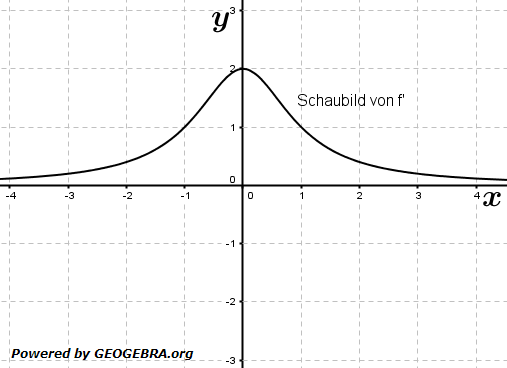
| Die Abbildung zeigt das Schaubild der Ableitungsfunktion f' einer Funktion f Welche der folgenden Aussagen über die Funktion f sind wahr, falsch oder unentscheidbar? |
 |
|
| (1) | f ist streng monoton wachsend für -3<x<3. | |
| (2) | Das Schaubild von f hat mindestens einen Wendepunkt. | |
| (3) | Das Schaubild von f ist symmetrisch zur y–Achse. | |
| (4) | Es gilt f(x)>0 für alle x ∈ [-3;3]. | |
| |
Aufgabe A4/05
Gegeben sind die Schaubilder der Funktion f mit f(x)=x2ex, ihrer Ableitungsfunktion f', einer Stammfunktion F von f und der Funktion g mit 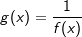 . . |
||||
 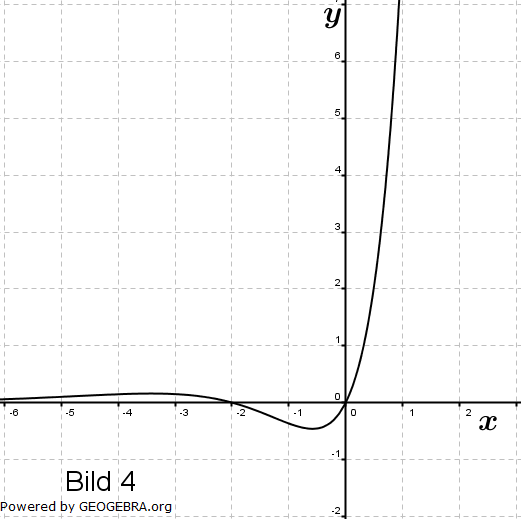 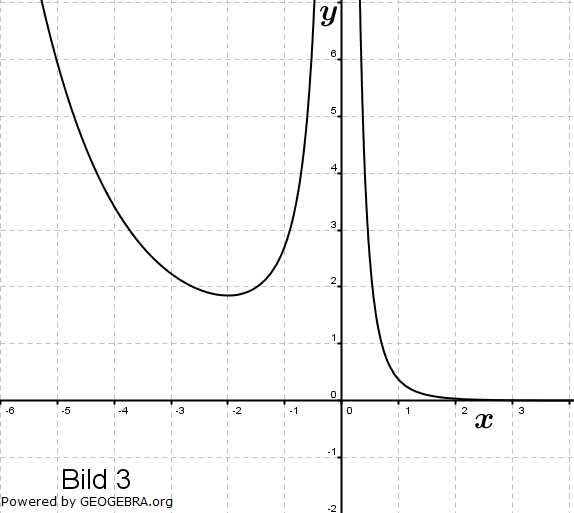 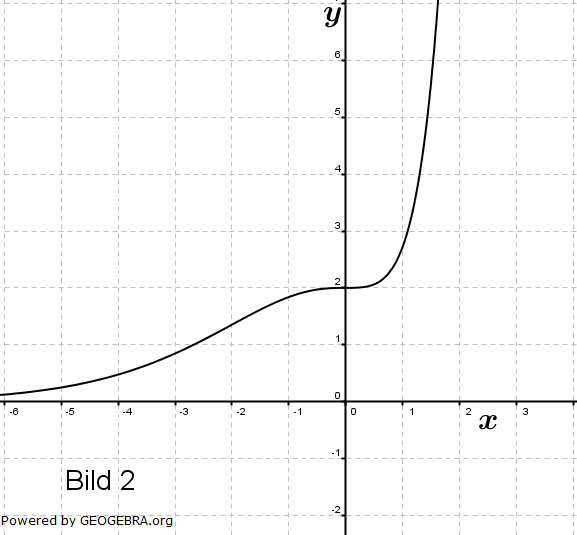 |
||||
|
| |
Aufgabe A4/06
| Die Abbildung zeigt das Schaubild der Ableitungsfunktion f' einer Funktion f. Geben Sie für jeden der folgenden Sätze an, ob er richtig, falsch oder nicht entscheidbar ist. |
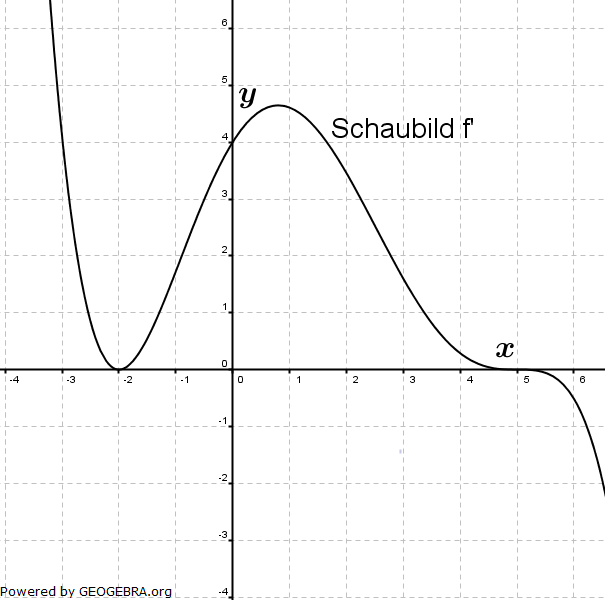 |
|
| (1) | Das Schaubild von f hat bei x=-2 einen Tiefpunkt. | |
| (2) | Das Schaubild von f hat für -3≤x≤6 genau zwei Wendepunkte. | |
| (3) | Das Schaubild von f verläuft im Schnittpunkt mit der y–Achse steiler als die erste Winkelhalbierende. | |
| (4) | f(0)>f(5). | |
| |
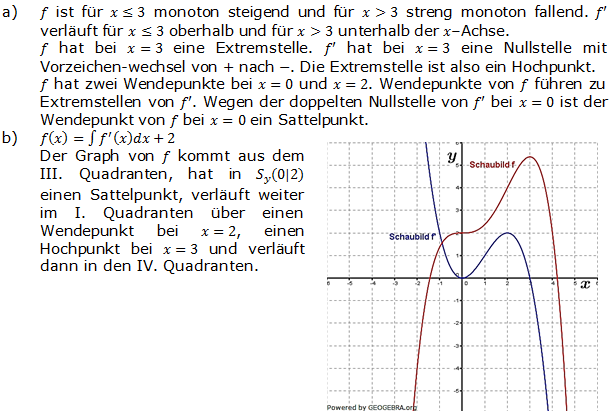
Aufgabe A4/07
| Gegeben ist das Schaubild der Ableitung f' der Funktion f. | 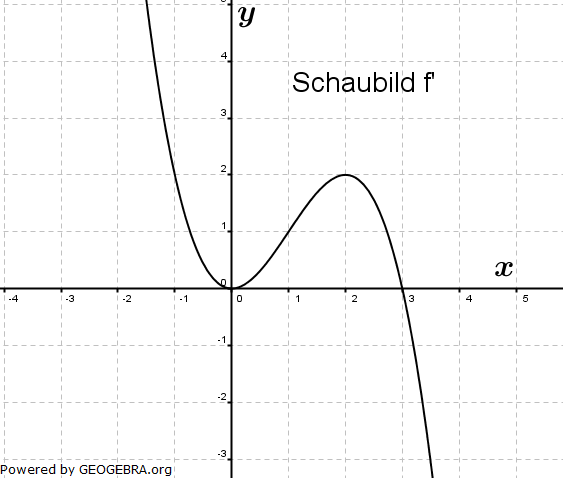 |
|
| a) | Welche Aussagen über die Funktion f ergeben sich daraus im Hinblick auf | |
| - Monotonie, - Extremstellen, - Wendestellen? Begründen Sie Ihre Aussagen. |
||
| b) | Es gilt f(0)=2. Skizzieren Sie das Schaubild von f. | |
| |
Aufgabe A4/08
Gegeben sind die Schaubilder von vier Funktionen, jeweils mit sämtlichen Asymptoten.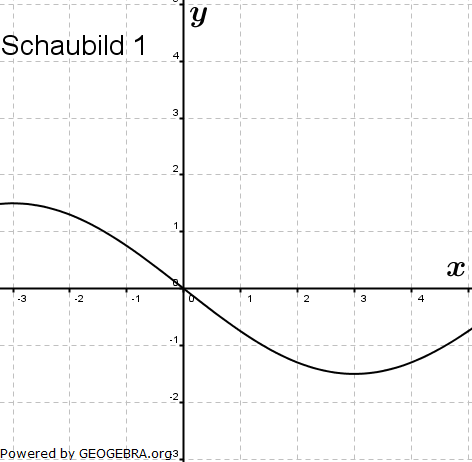 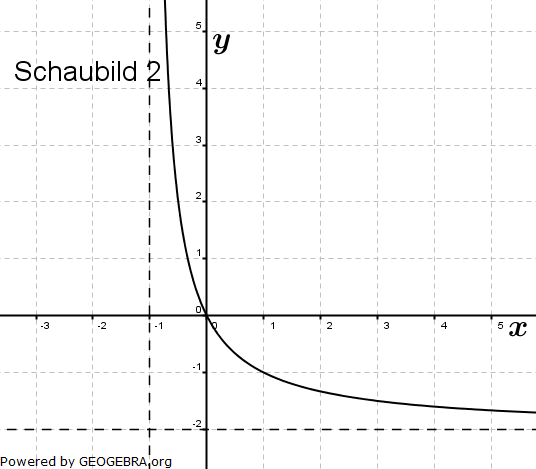 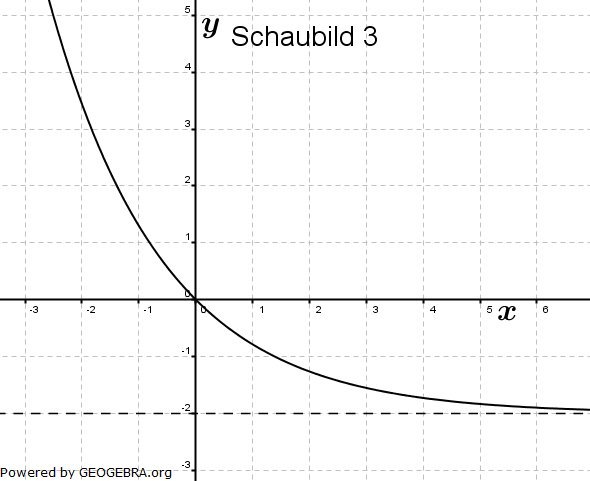 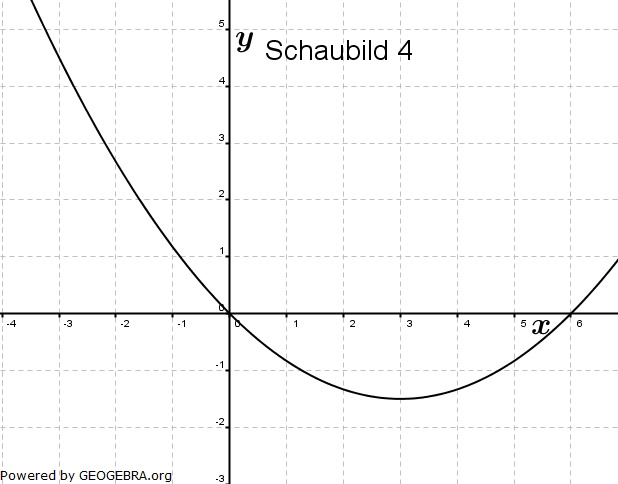 Drei dieser Schaubilder werden beschrieben durch die Funktionen f, g und h mit 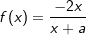 , g(x)=-2+b∙e-0,5x, h(x)=c∙x2-x , g(x)=-2+b∙e-0,5x, h(x)=c∙x2-x |
|
| a) | Ordnen Sie den Funktionen f, g und h das jeweils passende Schaubild zu. Begründen Sie Ihre Zuordnung. |
| b) | Bestimmen Sie die Werte für a, b und c. |
| |
Aufgabe A4/09
| Die Abbildung zeigt das Schaubild einer Funktion f. F ist eine Stammfunktion von f. | 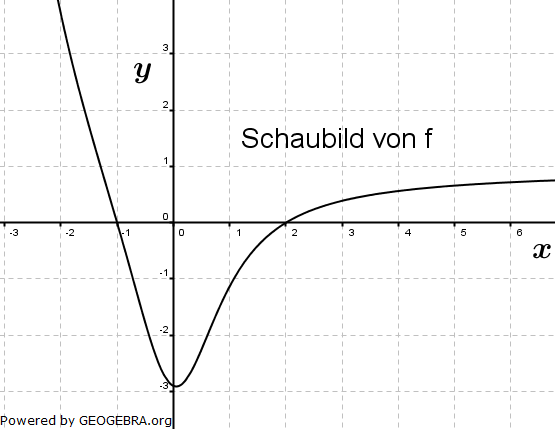 |
|
| a) | Welche Aussagen über F ergeben sich daraus um Bereich -2<x<7 hinsichtlich - Extremstellen, - Wendestellen, - Nullstellen? Begründen Sie Ihre Antworten. |
|
| b) | Begründen Sie, dass F(6)-F(2)>1 gilt. | |
| |
Aufgabe A4/10
| Die Abbildungen zeigen Schaubilder von Funktionen einschließlich aller waagrechten Asymptoten. Eines dieser Schaubilder gehört zur Funktion f mit 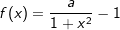 . . |
||||
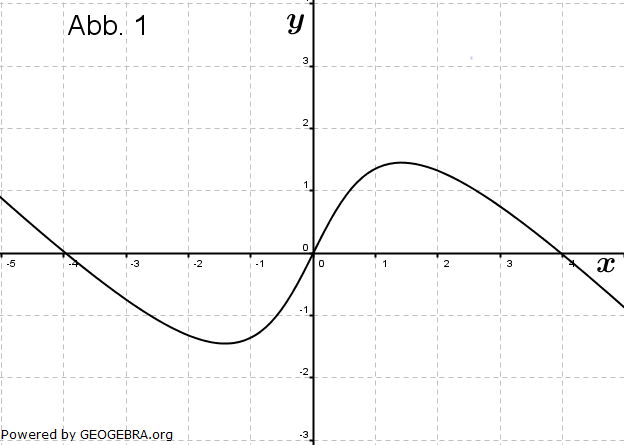 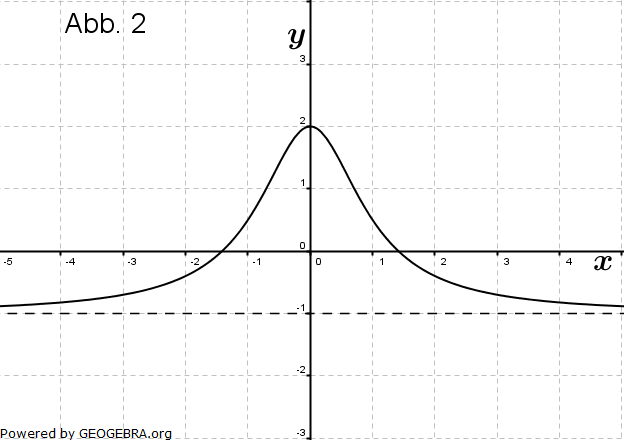 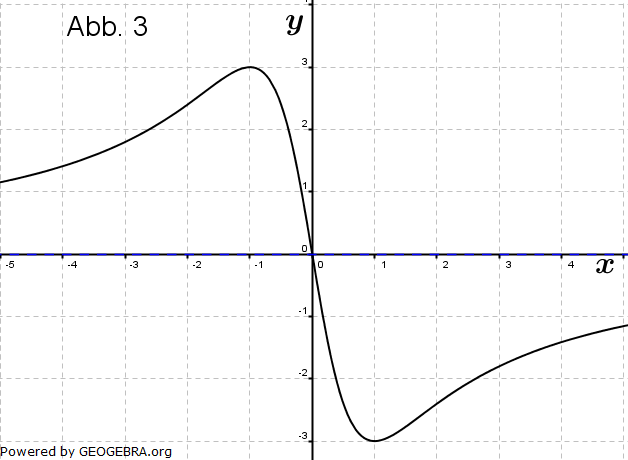 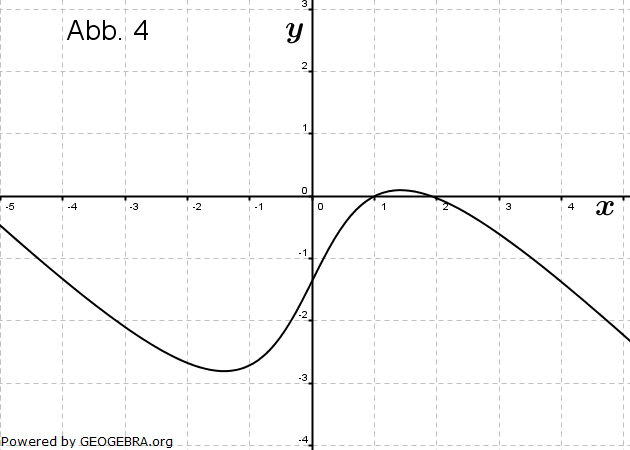
|
| |
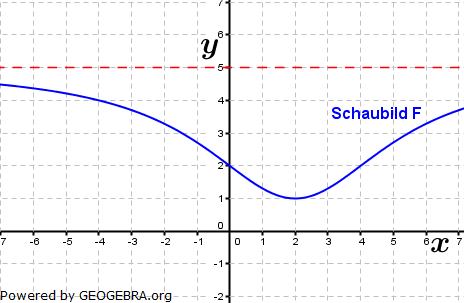
Aufgabe A4/11
| Die Abbildung zeigt das Schaubild einer Funktion f. F ist eine Stammfunktion von f. Begründen Sie, dass die folgenden Aussagen wahr sind: | 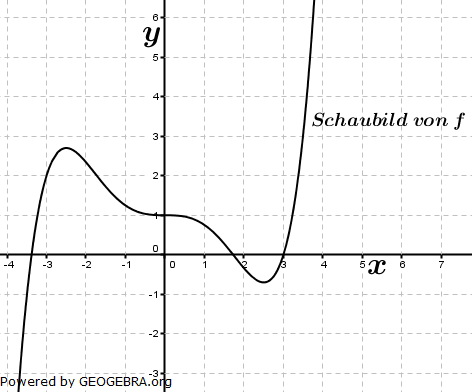 |
|
| (1) | F ist im Bereich -3≤x≤1 monoton wachsend. | |
| (2) | f' hat im Bereich -3,5≤x≤3,5 drei Nullstellen. | |
| (3) | 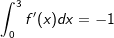 |
|
| (4) | O(0|0) ist der Hochpunkt des Schaubildes von f'. | |
Aufgabe A4/12
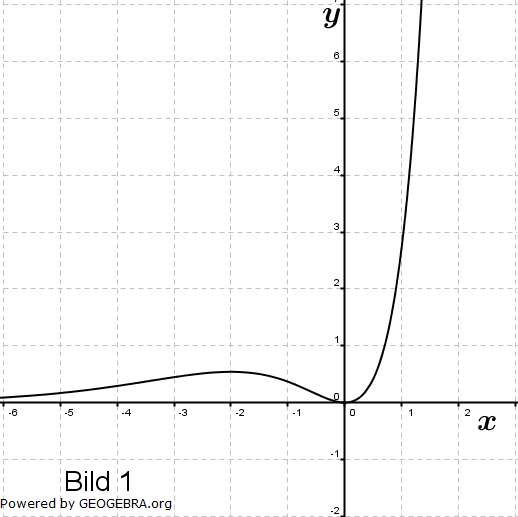
| Eine der folgenden Abbildungen zeigt den Graphen der Funktion f mit f(x)=x3-3x-2. | |
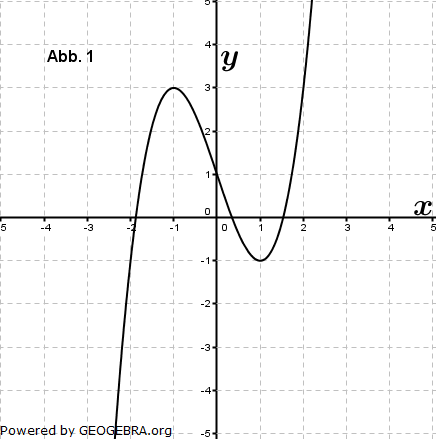 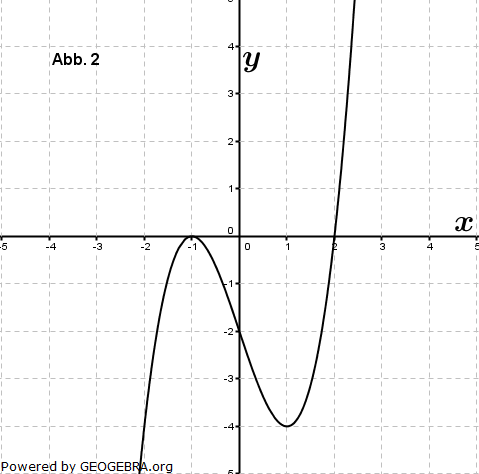 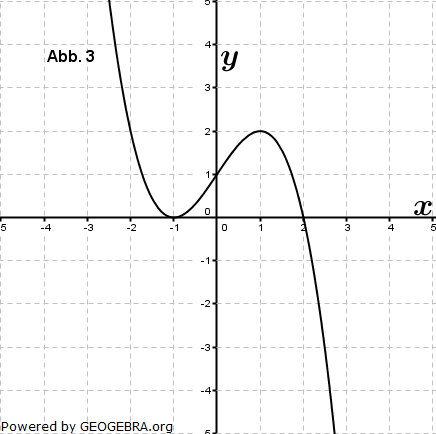 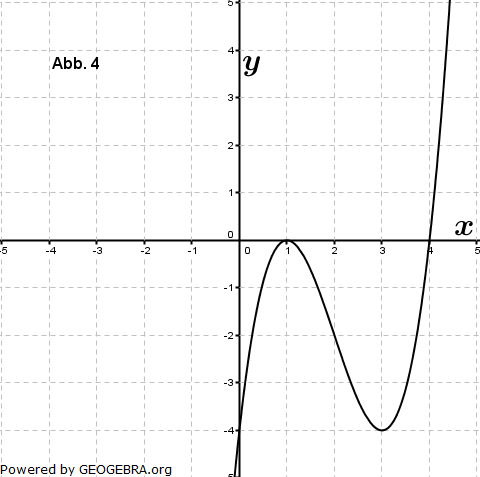 |
|
| a) | Begründen Sie, dass die Abbildung 2 den Graphen von f zeigt. |
| b) | Von den anderen drei Abbildungen gehört eine zur Funktion g mit g(x)=f(x-a) und eine zur Funktion h mit h(x)=b∙f(x). Ordnen Sie diesen beiden Funktionen die zugehörigen Abbildungen zu und begründen Sie Ihre Entscheidung. Geben Sie die Werte für a und b an. |
| |
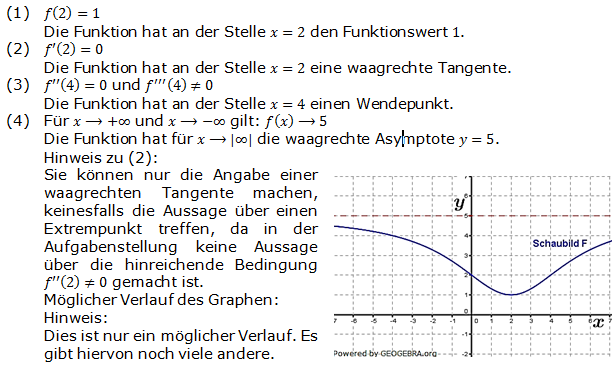
Aufgabe A4/13
Eine Funktion f hat die folgenden Eigenschaften:
Skizzieren Sie einen möglichen Verlauf des Graphen. |
| |
Aufgabe A4/14
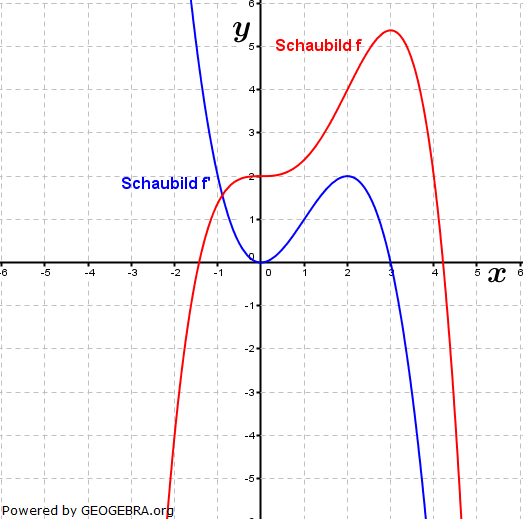
| Die Abbildung zeigt die Graphen Kf und Kg zweier Funktionen f und g. | 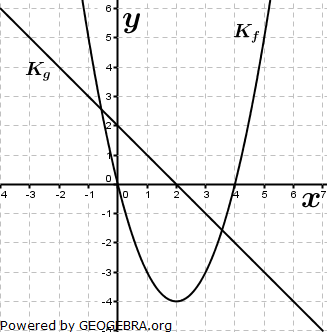 |
|
| a) | Bestimmen Sie f(g(3)). Bestimmen Sie einen Wert für x so, dass f(g(x))=0 ist. |
|
| b) | Die Funktion h ist gegeben durch h(x)=f(x)⋅g(x). Bestimmen Sie h'(2). |
|
| |
Aufgabe A4/15
| Die Abbildung zeigt den Graphen der Ableitungsfunktion einer ganzrationalen Funktion f. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind. Bergründen Sie jeweils Ihre Antwort. |
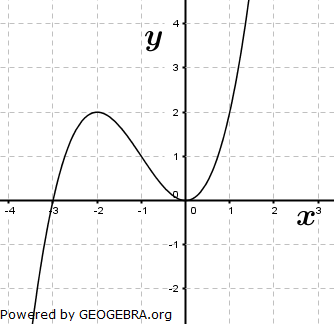 |
|
| (1) | Der Graph von f hat bei x=-3 einen Tiefpunkt. | |
| (2) | f(-2)<f(-1) | |
| (3) | f''(-2)+f'(-2)<1 | |
| (4) | Der Grad der Funktion f ist mindestens 4. | |
| |
Aufgabe A4/16
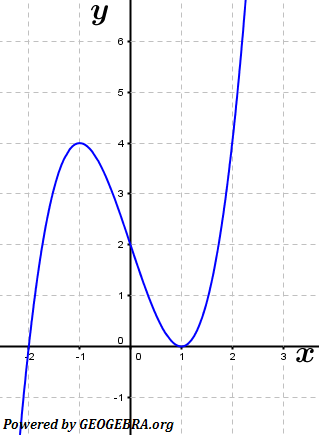
| Die Abbildung zeigt den Graphen einer Stammfunktion F einer Funktion f. Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Bergründen Sie jeweils Ihre Entscheidung. |
 |
|
| (1) | f(1)=F(1) | |
| (2) |  |
|
| (3) | f' besitzt im Bereich -1≤x≤1 eine Nullstelle. | |
| (4) | f(F(-2))>0 | |
| |
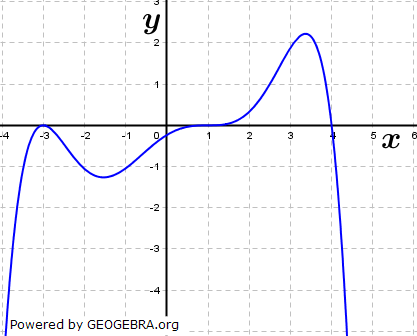
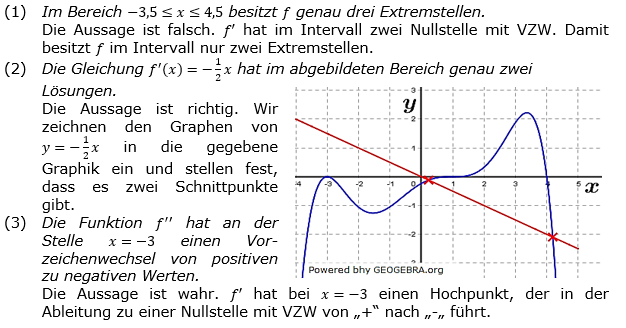
Aufgabe A4/18
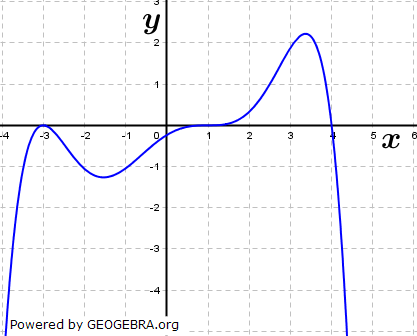
| Die Abbildung zeigt den Graphen der Ableitungsfunktion f' einer ganzrationalen Funktion f. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind. Begründen Sie jeweils Ihre Antwort. |
 |
|
| (1) | Im Bereich -3,5≤x≤4,5 besitzt f genau drei Extremstellen. | |
| (2) | Die Gleichung 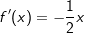 hat im abgebildeten Bereich genau zwei Lösungen. hat im abgebildeten Bereich genau zwei Lösungen. |
|
| (3) | Die Funktion f'' hat an der Stelle x=-3 einen Vorzeichenwechsel von positiven zu negativen Werten. | |
| |
| Du befindest dich hier: |
| Grafisch Differenzieren|Integrieren Pflichtteil allg. Gymnasium 2004-2018 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. September 2019 16. September 2019











 .
.