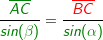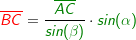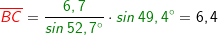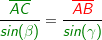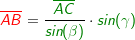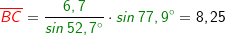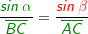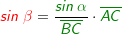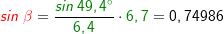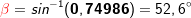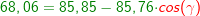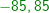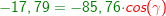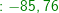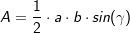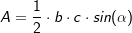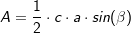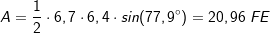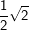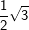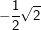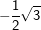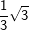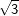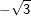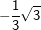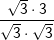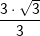|
Trigonometrie Realschulabschluss |
Realschulabschluss Trigonometrie | Themenerläuterung
aaa(linke Maustaste zum Schließen/Öffnen)
| Im Kapitel Trigonometrie bekommst du Zeichnungen von zusammengesetzten Figuren aus Dreiecken, Quadraten, Rechtecken, Parallelogrammen, Trapezen und eventuell Kreisbögen. Einige Streckenlängen und/oder einige Winkel der Figuren werden vorgegeben. Du sollst an Hand dieser Angaben andere Strecken, Winkel und Flächeninhalte von Teilfiguren berechnen. Die Lösung dieser Aufgaben ist in den meisten Fällen nur über Teildreiecke der Figuren möglich. Dabei handelt es sich um rechtwinklige Dreiecke oder allgemeine Dreiecke. Oftmals musst du diese Dreiecke durch geeignete Hilfslinien bilden, um an die geforderten Ergebnisse zu gelangen. Dabei beachte bitte Folgendes: Bei rechtwinkligen Dreiecken verwendest du die trigonometrischen Funktionen sin, cos und tan sowie den Satz des Pythagoras. Bei allgemeinen Dreiecken, also Dreiecken, in denen kein rechter Winkel vorhanden ist, benutzt du am schnellsten den Sinussatz bzw. Kosinussatz und für Flächenberechnungen die Formel des trigonometrischen Flächeninhalts (siehe nachfolgend „Die wichtigsten benötigten Formeln“). Beachte auch bitte: Alle erforderlichen Formeln stehen in der Formelsammlung mit Ausnahme des Kosinussatzes. Da die Verwendung des Sinus- und des Kosinussatzes in vielen Fällen den Rechenweg wesentlich vereinfacht, solltest du dir den Kosinussatz gut einprägen. Im nächsten Thema wird der Sinus- und Kosinussatz sowie der trigonometrische Flächeninhalt nochmals ausführlich erläutert. Bei den einzelnen Aufgaben erhältst du jeweils einen Hinweis/Tipp, ob eine schnellere Lösung mit dem Sinus- bzw. Kosinussatz möglich ist. Die Lösungsteile der Aufgaben sind in diesen Fällen aufgeteilt in die einfache Lösung und in die herkömmliche – als umständlich gekennzeichnet – Lösung. |
Die wichtigsten benötigten Formeln
....(linke Maustaste zum Schließen/Öffnen)
1. Der Satz des Pythagoras
| Ist im rechtwinkligen Dreieck c die Hypothenuse (= längste Seite) und a und b die beiden Katheten, so gilt: |
c2=a2+b2 bzw. 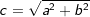 |
a2=c2-b2 bzw. 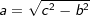 |
b2=c2-a2 bzw. 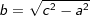 |
2. Die trigonometrischen Formeln
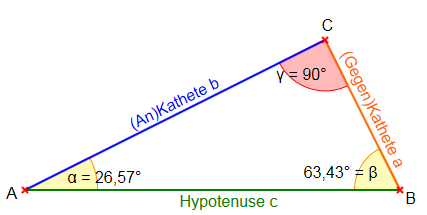 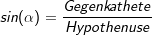 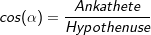 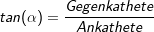 Die Hypothenuse ist immer die längste Seite im rechtwinkligen Dreieck und liegt dem rechten Winkel gegenüber. Die Gegenkathete ist die Kathete, die dem Winkel, um den es geht, gegenüber liegt. Die Ankathete ist die Kathete, die an dem Winkel, um den es geht, anliegt. |
3. Die Flächenformeln
| Dreieck: | 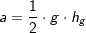 mit g als Grundseite und hg als Höhe auf die Grundseite. mit g als Grundseite und hg als Höhe auf die Grundseite.Beim rechtwinkligen Dreieck ist die eine Kathete die Grundseite und die andere Kathete die Höhe auf diese Grundseite. |
| Quadrat: | A=a2 mit a als der Seitenlänge. |
| Rechteck: | A=a⋅b mit a und b als die beiden Seitenlängen des Rechtecks. |
| Parallelogramm: | A=a⋅ha bzw. b⋅hb mit a bzw. b als eine der beiden Seiten des Parallelogramms und ha bzw hb als Höhe auf die jeweilige Seite. |
| Trapez: | 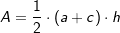 mit a und c als den beiden parallelen Seiten des Trapezes und h als Höhe auf diese Seiten. mit a und c als den beiden parallelen Seiten des Trapezes und h als Höhe auf diese Seiten. |
| Drachen/Raute: | 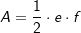 mit e und f als den beiden Diagonalen. mit e und f als den beiden Diagonalen. |
4. Der Sinussatz
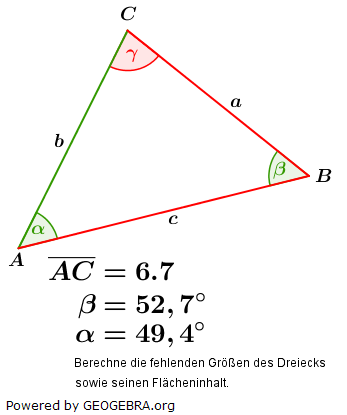 Im allgemeinen Dreieck gilt: Im allgemeinen Dreieck gilt: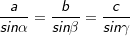 Diese allgemeine Form des Sinussatzes lässt sich aber nur sehr schwer merken. Deshalb bilden wir uns eine „Eselsbrücke“. Für die Anwendung des Sinussatzes brauchst du eine bekannte Seite (im Beispiel die Seite 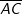 und den dieser Seite gegenüberliegenden bekannten Winkel (im Beispiel ist dies β), eine zweite unbekannte Seite (im Beispiel die Strecke und den dieser Seite gegenüberliegenden bekannten Winkel (im Beispiel ist dies β), eine zweite unbekannte Seite (im Beispiel die Strecke 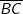 ) und einen dieser Seite gegenüberliegenden bekannten Winkel (im Beispiel α). Mit dem Sinussatz kannst du nun die unbekannte Seite direkt ausrechnen, indem du schreibst: ) und einen dieser Seite gegenüberliegenden bekannten Winkel (im Beispiel α). Mit dem Sinussatz kannst du nun die unbekannte Seite direkt ausrechnen, indem du schreibst: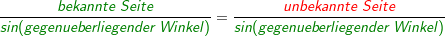
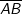 bestimmen. Jetzt ist wie zuvor bestimmen. Jetzt ist wie zuvor  die bekannte Seite und β der gegenüberliegende bekannte Winkel, die bekannte Seite und β der gegenüberliegende bekannte Winkel,  die unbekannte Seite und γ der gegenüberliegende bekannte Winkel, also die unbekannte Seite und γ der gegenüberliegende bekannte Winkel, also
 Natürlich kannst du mit dem Sinussatz auch unbekannte Winkel bestimmen. Hierzu haben wir jetzt die bekannte Strecke Natürlich kannst du mit dem Sinussatz auch unbekannte Winkel bestimmen. Hierzu haben wir jetzt die bekannte Strecke  und den bekannten gegenüberliegenden Winkel α, die bekannte Strecke und den bekannten gegenüberliegenden Winkel α, die bekannte Strecke  und den unbekannten gegenüberliegenden Winkel β. Wie bilden nun das Verhältnis über den Sinussatz mit und den unbekannten gegenüberliegenden Winkel β. Wie bilden nun das Verhältnis über den Sinussatz mit
|
||||||||||||||||||||||||||||||||||||||||||
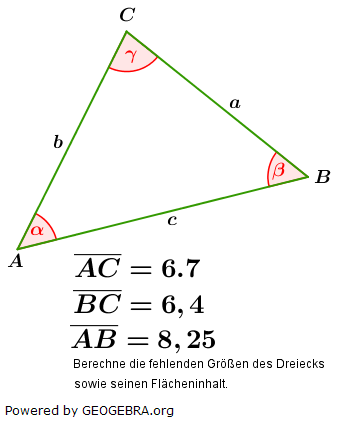
5. Der Kosinussatz
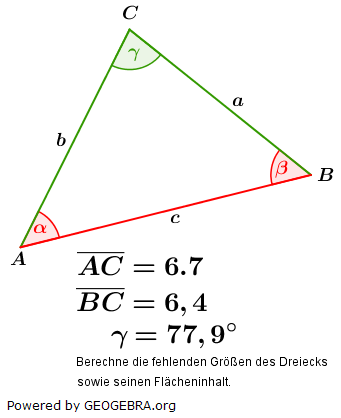 Im allgemeinen Dreieck gilt c2=a2+b2-2ab⋅cosγ bzw. Im allgemeinen Dreieck gilt c2=a2+b2-2ab⋅cosγ bzw.  . Diese allgemeine Form des Kosinussatzes lässt sich auch nur sehr schwer merken. Deshalb bilden wir uns erneut eine „Eselsbrücke“. . Diese allgemeine Form des Kosinussatzes lässt sich auch nur sehr schwer merken. Deshalb bilden wir uns erneut eine „Eselsbrücke“. Für die Anwendung des Kosinussatzes brauchst du zwei bekannte Seite (im Beispiel die Seiten  und und  ) und den von diesen Seiten eingeschlossenen bekannten Winkel (im Beispiel ist dies ) und den von diesen Seiten eingeschlossenen bekannten Winkel (im Beispiel ist dies  ) Mit dem Kosinussatz kannst du nun die unbekannte dritte Seite direkt ausrechnen, indem du schreibst: ) Mit dem Kosinussatz kannst du nun die unbekannte dritte Seite direkt ausrechnen, indem du schreibst: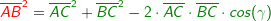 Wir setzen Zahlen ein und erhalten: 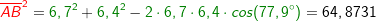 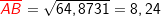 Die restlichen Werte des Dreiecks können nun mühelos über den Sinussatz ermittelt werden. 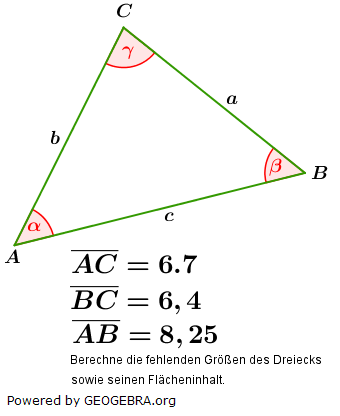 Natürlich kannst du mit dem Kosinussatz auch unbekannte Winkel bestimmen. Hierzu müssen alle drei Seiten des Dreiecks bekannt sein. Wir entscheiden uns zur Berechnung des Winkels Natürlich kannst du mit dem Kosinussatz auch unbekannte Winkel bestimmen. Hierzu müssen alle drei Seiten des Dreiecks bekannt sein. Wir entscheiden uns zur Berechnung des Winkels  und bilden: und bilden: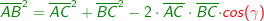 Wir setzen Zahlen ein: 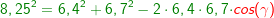
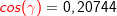 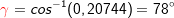 Die restlichen Werte des Dreiecks lassen sich dann wieder einfach über den Sinussatz berechnen. |
6. Trigonometrischer Flächeninhalt
 Im allgemeinen Dreieck gilt für dessen Flächeninhalt: Im allgemeinen Dreieck gilt für dessen Flächeninhalt:
Du benötigst zur Flächenberechnung mithilfe des trigonometrischen Flächeninhaltes zwei bekannte Seite (im Beispiel die Seiten  und und  ) und den von diesen Seiten eingeschlossenen bekannten Winkel (im Beispiel ist dies ) und den von diesen Seiten eingeschlossenen bekannten Winkel (im Beispiel ist dies  ). ).
|
7. Besondere Werte für sin, cos und tan
| In bestimmten Aufgaben sollst du den Nachweis eines Flächeninhalts, des Umfangs einer Figur, der Länge einer Strecke oder gar dem Wert eines sin, cos bzw. tan führen in Abhängigkeit einer sogenannten „Formvariablen“. Diese Formvariable wird mit dem Buchstaben "e" bezeichnet. In diesen Aufgaben wird verlangt, dass du den Nachweis ohne gerundete Werte führen sollst. Dies bedeutet für dich, dass du keinen Taschenrechner verwenden kannst und die Aufgabe manuell lösen musst. In diesen Aufgaben handelt es sich stets nur um Winkel der Größe 30° , 45° , 60° bzw. 90° . Für diese Winkelgrößen gibt es besondere Werte, die in nachstehender Tabelle aufgeführt sind. Diese Tabelle findest du auch in deiner Formelsammlung.
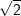 bzw. bzw. 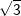 vor – kann es vorkommen, dass du zum Erreichen der korrekten Lösung der Aufgabe oftmals den Nenner eines Bruchs rational machen musst, weshalb dies hier nochmals aufgeführt wird. vor – kann es vorkommen, dass du zum Erreichen der korrekten Lösung der Aufgabe oftmals den Nenner eines Bruchs rational machen musst, weshalb dies hier nochmals aufgeführt wird. Angenommen, du erhältst ein Ergebnis wie etwa 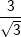 . Das geforderte Ergebnis laut Aufgabe soll aber . Das geforderte Ergebnis laut Aufgabe soll aber 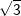 sein. Du musst jetzt erkennen, dass man eine Wurzel im Nenner eines Bruchs nicht stehenlassen darf, die Wurzel im Nenner muss verschwinden. Dies wird als „Rationalmachen eines Nenners“ verstanden, was so erfolgt, dass du den Bruch mit der Wurzel im Nenner um diesen Wert erweitern musst. sein. Du musst jetzt erkennen, dass man eine Wurzel im Nenner eines Bruchs nicht stehenlassen darf, die Wurzel im Nenner muss verschwinden. Dies wird als „Rationalmachen eines Nenners“ verstanden, was so erfolgt, dass du den Bruch mit der Wurzel im Nenner um diesen Wert erweitern musst. Für unser Beispiel 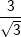 bedeutet dies: bedeutet dies:
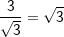 . . |
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |