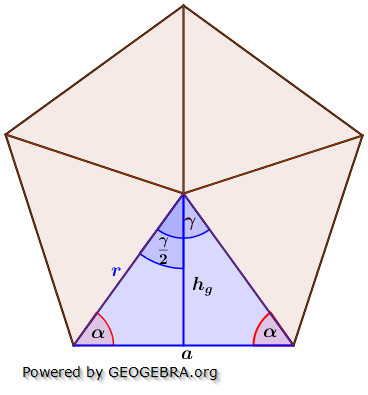
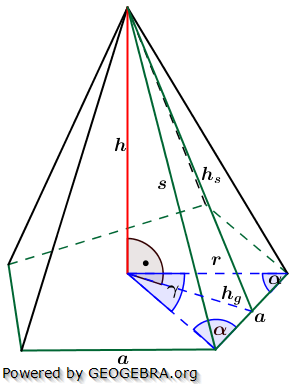
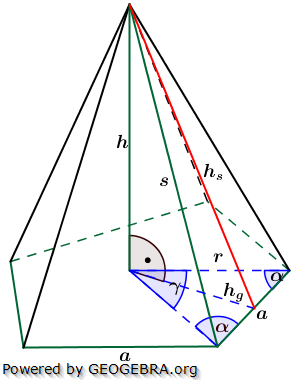
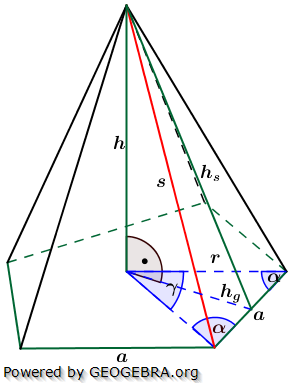
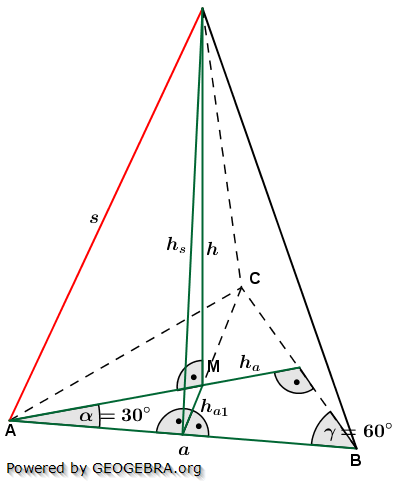
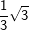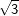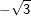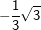 Die nachfolgenden Regeln und Formeln werden beispielhaft an einer 5-Eckpyramide erläutert. Grundlage der Betrachtung ist dabei die Grundfläche, die ja aus einem regelmäßigen n-Eck besteht. Die nachfolgenden Regeln und Formeln werden beispielhaft an einer 5-Eckpyramide erläutert. Grundlage der Betrachtung ist dabei die Grundfläche, die ja aus einem regelmäßigen n-Eck besteht.
Wie du aus der Grafik erkennst, ist die Grundfläche des n-Ecks in n kongruente Dreiecke unterteilt. Diese Dreiecke sind gleichschenklig, das heißt, a ist die Grundeite und r sind die beiden gleich langen Schenkel jeden Dreiecks. hg ist die Höhe dieser n Dreiecke. γ ist der Spitzenwinkel und α ist der Basiswinkel. Wenn du nun die n Spitzenwinkel zusammenzählst, müssen ja 360° herauskommen, denn einmal um die Mittelpunkt herum entspricht ja 360°.
Aus dieser Gesetzmäßigkeit heraus kannst du in jeder n–Eckaufgabe sofort die Größe der Winkel α und γ bestimmen, denn es gilt:
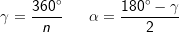
Hast du die Winkel bestimmt, steht der Berechnung der Seitenlänge r sowie der Grundflächendreieckshöhe hg nichts mehr im Wege.
Berechnung von r:
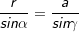 ⟹ ⟹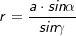 |
|
Sinussatz 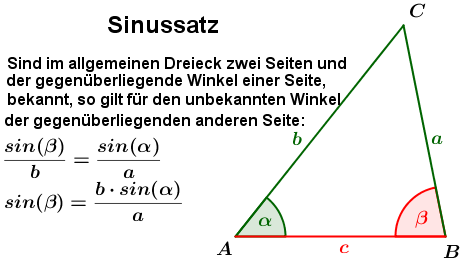 |
oder
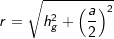 |
|
Satz des Pythagoras 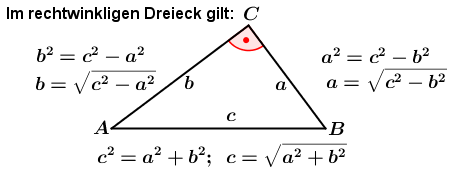 |
Für letzteres benötigst du jedoch zuerst die Berechnung von hg.
Berechnung von hg:
 ⟹ ⟹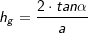 |
Weiterhin ermöglicht dir dies jetzt auch die Berechnung der Fläche des regelmäßigen n–Ecks.
Die Fläche eines einzelnen Teildreiecks ist: |
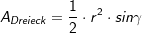 |
|
trigonometrischer Flächeninhalt 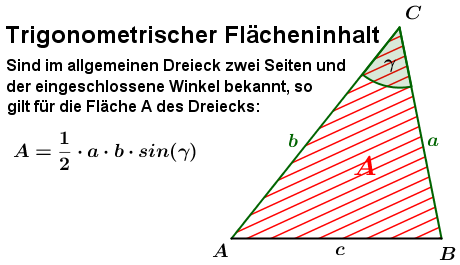 |
oder
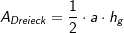
und hieraus dann die Fläche des n-Ecks:
 bzw. bzw. 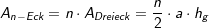 . . |
5.1 Volumen, Oberfläche, Mantel
 Das Volumen einer regelmäßigen n-Eckpyramide errechnet sich aus Das Volumen einer regelmäßigen n-Eckpyramide errechnet sich aus 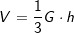 mit mit 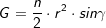 (Fläche eines regelmäßigen n-Ecks), somit: (Fläche eines regelmäßigen n-Ecks), somit: 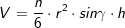 . .
Alternativ 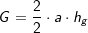 somit: somit:
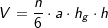 . a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide. . a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
Der Mantel der Pyramide errechnet sich aus 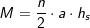 , a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks. , a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
Die Oberfläche der Pyramide errechnet sich aus O=G+M somit:
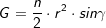 und und 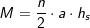 . .
Alternativ: 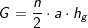 und und 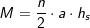 . .
a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks. |
5.2 Höhe h
Welche Werte vorgegeben sind, bestimmt die Rechenoperation zur Ermittlung der Höhe h:
| a) |
aus dem Volumen über 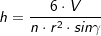 , alternativ , alternativ 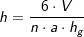 . . |
| b) |
über die Seitenkante s eines Seitendreiecks und der Länge a der Grundfläche mit  . . |
| c) |
über die Höhe hs eines Seitendreicks und der Höhe hg eines Teildreiecks der Grundfläche  mit mit 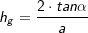 , a ist Seitenkante der Grundfläche. , a ist Seitenkante der Grundfläche. |
|
 |
5.3 Höhe hS
Welche Werte vorgegeben sind bestimmt die Rechenoperation der Höhe hs der Seitendreiecke:
| a) |
aus dem Mantel über 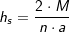 , a ist Seitenkante der Grundfläche. , a ist Seitenkante der Grundfläche. |
| b) |
über die Seitenkante s der Pyramide und der Seitenkante a des n-Ecks mit 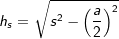 . . |
| c) |
über die Höhe h der Pyramide und der Höhe hg eines Teildreiecks der Grundfläche 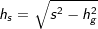 mit mit 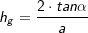 , a ist Seitenkante der Grundfläche. , a ist Seitenkante der Grundfläche. |
|
 |
5.4 Kante s
Welche Werte vorgegeben sind bestimmt die Rechenoperation der Länge s der Seitenkante der Seitendreiecke:
| a) |
über die Höhe h der Pyramide und der Länge r der Seitenkante eines Teildreiecks der Grundfläche mit 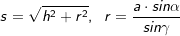 . . |
| b) |
über die Höhe hs der Seitendreiecke und der halben Länge a mit 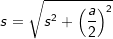 , a ist die Seitenkante der Grundfläche. , a ist die Seitenkante der Grundfläche. |
|
 |
|

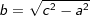
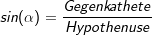
 Die nachfolgenden Regeln und Formeln werden beispielhaft an einer 5-Eckpyramide erläutert. Grundlage der Betrachtung ist dabei die Grundfläche, die ja aus einem regelmäßigen n-Eck besteht.
Die nachfolgenden Regeln und Formeln werden beispielhaft an einer 5-Eckpyramide erläutert. Grundlage der Betrachtung ist dabei die Grundfläche, die ja aus einem regelmäßigen n-Eck besteht. 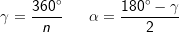

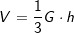 mit
mit 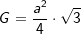 (Fläche eines gleichseitigen Dreiecks), a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
(Fläche eines gleichseitigen Dreiecks), a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide. 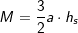 , a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks. 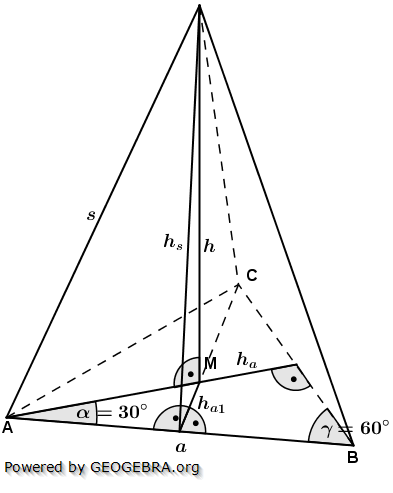
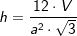 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche. mit
mit 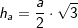 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.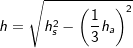 mit
mit 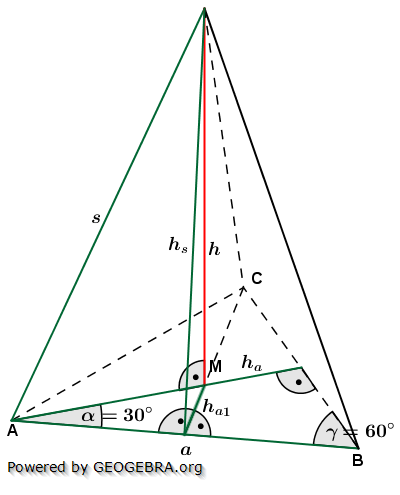
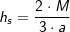 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.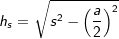 .
.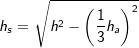 mit
mit 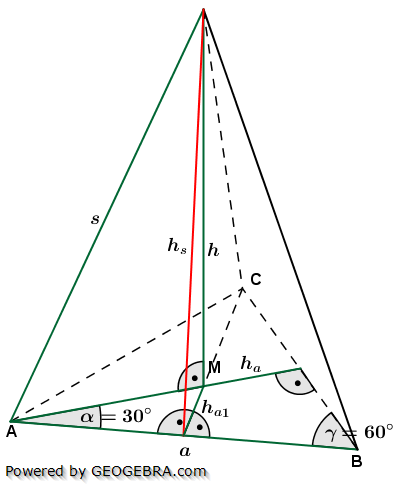
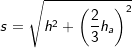 mit
mit 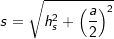 .
.
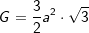 (Fläche eines regelmäßigen Sechsecks), somit
(Fläche eines regelmäßigen Sechsecks), somit 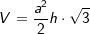 . a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
. a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.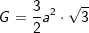 und M=3a⋅hs, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
und M=3a⋅hs, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.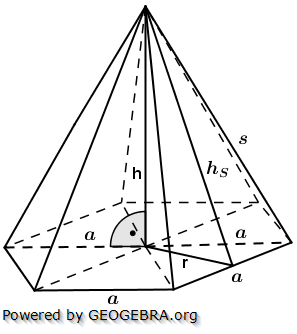
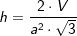 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.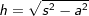 .
.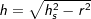 mit
mit 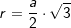 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.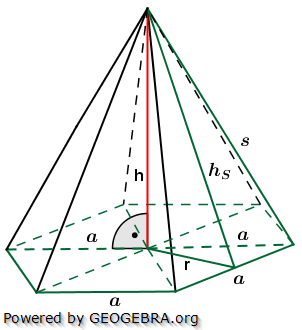
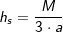 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.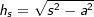 .
.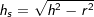 mit
mit 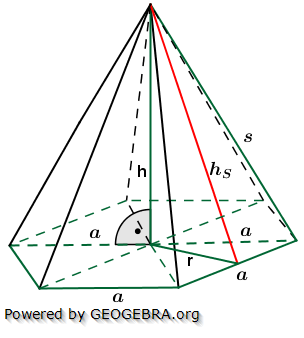
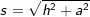 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.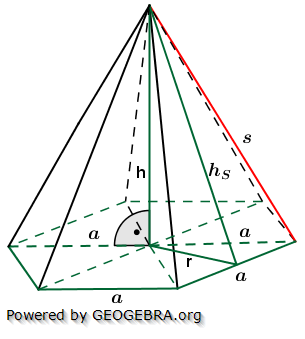
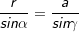 ⟹
⟹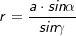

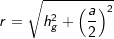

 ⟹
⟹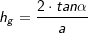
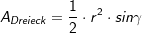

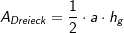
 bzw.
bzw. 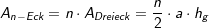 .
. Das Volumen einer regelmäßigen n-Eckpyramide errechnet sich aus
Das Volumen einer regelmäßigen n-Eckpyramide errechnet sich aus 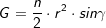 (Fläche eines regelmäßigen n-Ecks), somit:
(Fläche eines regelmäßigen n-Ecks), somit: 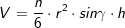 .
.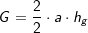 somit:
somit: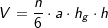 . a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.
. a ist Seitenkante der Grundfläche, h ist die Höhe der Pyramide.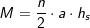 , a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.
, a ist Seitenkante der Grundfläche, hs ist die Höhe eines Seitendreiecks.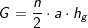 und
und 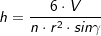 , alternativ
, alternativ 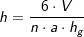 .
. .
. mit
mit 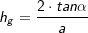 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.
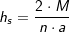 , a ist Seitenkante der Grundfläche.
, a ist Seitenkante der Grundfläche.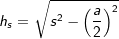 .
.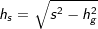 mit
mit 
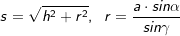 .
.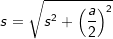 , a ist die Seitenkante der Grundfläche.
, a ist die Seitenkante der Grundfläche.