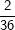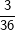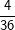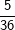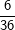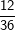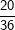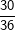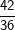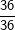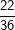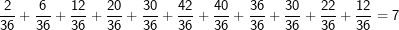|
Zufall und Wahrscheinlichkeit Realschulabschluss |

Realschulabschluss Zufall / Wahrscheinlichkeit | Themenerläuterung
aaa(linke Maustaste zum Schließen/Öffnen)
| Dieses Thema handelt von der Berechnung der relativen Häufigkeit (Wahrscheinlichkeit) des Auftretens bestimmter Ereignisse bei Zufallsexperimenten. Unter einem Zufallsexperiment wird z.B. das Ziehen von Kugeln unterschiedlicher Farben aus einer Urne verstanden, oder das Werfen einer Münze, oder das Würfeln von zwei Würfeln, oder das Drehen eines Glücksrades usw. Das Auftreten des Ergebnisses eines Zufallsexperiments wird als Ereignis bezeichnet. Die Summe aller möglichen Ereignisse eines Zufallsexperiments bezeichnet man als Ergebnisraum des Experiments. So hat z.B. das Werfen einer Münze die Ereignisse „Wappen“ und „Zahl“. Der Ergebnisraum dieses Experiments hat damit die Anzahl 2, da ja nur die genannten beiden Ereignisse auftreten können. Die grafische Veranschaulichung aller möglichen Ereignisse eines Zufallsexperiments erfolgt häufig über sogenannte „Baumdiagramme“. Die einzelnen Ereignisse werden durch relative Häufigkeiten, der sogenannten „Wahrscheinlichkeit“ beschrieben. Die Wahrscheinlichkeit für „Wappen“ beim Werfen einer Münze beträgt 0,5=50%, da ja nur zwei Ereignisse auftreten können. Beim Werfen eines Würfels hat das Auftreten einer 6 die Wahrscheinlichkeit 1/6, da beim Würfel ja die Ereignisse 1, 2, 3, 4, 5 oder 6 auftreten können. Wir unterscheiden noch nach einstufigen, zweistufigen usw. bzw. mehrstufigen Zufallsexperimenten und zusätzlich noch zwischen Ziehen „mit Zurücklegen“ und „ohne Zurücklegen“. Je nach Art des Zufallsexperiments gelten unterschiedlich Regeln für die Berechnung der Wahrscheinlichkeit eines Ereignisses. Ereignisse werden mit großen Buchstaben beschrieben, z. B. E: „Werfen einer 6 beim Würfeln mit einem Würfel“ Die zugehörige Wahrscheinlichkeit wird dann mit P(E) bezeichnet. |
Die wichtigsten benötigten Formeln / Begriffe
aaa(linke Maustaste zum Schließen/Öffnen)
1. Summe aller Wahrscheinlichkeiten
| Die Summe aller möglichen Ereignisse eines Zufallsexperiments ist stets 1 bzw. 100 %. |
2. Baumdiagramme und Pfadregeln
Ziehen mit Zurücklegen
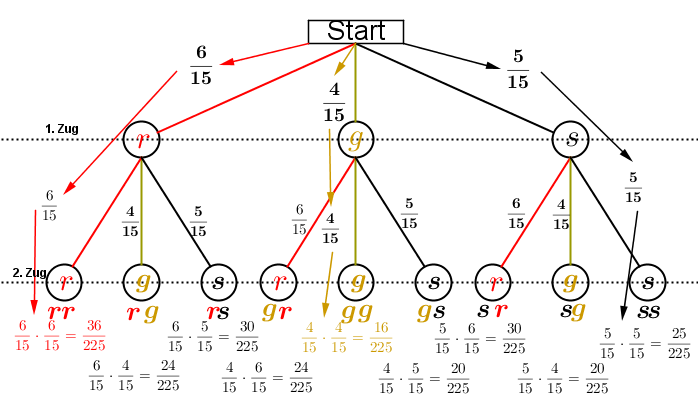 Das vorstehende Baumdiagramm zeigt das zweimalige Ziehen von Kugeln aus einer Urne mit 6 roten, 4 gelben und 5 schwarzen Kugeln mit Zurücklegen. An den einzelnen Ästen steht jeweils die Wahrscheinlichkeit für den jeweiligen Zug. Das Ziehen einer roten Kugel hat die Wahrscheinlichkeit Das vorstehende Baumdiagramm zeigt das zweimalige Ziehen von Kugeln aus einer Urne mit 6 roten, 4 gelben und 5 schwarzen Kugeln mit Zurücklegen. An den einzelnen Ästen steht jeweils die Wahrscheinlichkeit für den jeweiligen Zug. Das Ziehen einer roten Kugel hat die Wahrscheinlichkeit 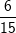 , denn es gibt 6 rote von insgesamt 15 Kugeln. Für die gelbe Kugel ist die Wahrscheinlichkeit , denn es gibt 6 rote von insgesamt 15 Kugeln. Für die gelbe Kugel ist die Wahrscheinlichkeit 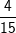 , denn es gibt 4 gelbe von insgesamt 15 Kugeln. Für die schwarze Kugel ist die Wahrscheinlichkeit , denn es gibt 4 gelbe von insgesamt 15 Kugeln. Für die schwarze Kugel ist die Wahrscheinlichkeit 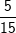 , denn es gibt 5 schwarze von insgesamt 15 Kugeln. , denn es gibt 5 schwarze von insgesamt 15 Kugeln. |
Ziehen ohne Zurücklegen
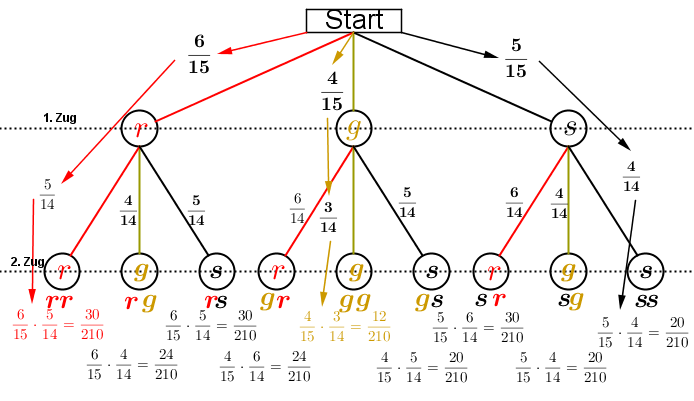 Dieses Baumdiagramm entspricht dem Baumdiagramm aus „Ziehen ohne Zurücklegen“ mit dem Unterschied, dass jetzt die erste gezogene Kugel nicht in die Urne zurückgelegt wird, wir sprechen von „Ziehen ohne Zurücklegen“. Im ersten Zug bleibt alles wie es war, jedoch verändern sich jetzt die Wahrscheinlichkeiten an den Ästen des zweiten Zuges. Da die zuerst gezogene Kugel ja nicht zurückgelegt wird, befinden sich für den zweiten Zug ja nur noch 14 Kugeln in der Urne. Wurde zuerst eine rote Kugel gezogen, befinden sich nur noch 5 rote Kugeln in der Urne, jedoch weiterhin 4 gelbe und 5 schwarze. Analog gilt dies für das Ziehen einer gelben oder schwarzen Kugel im ersten Zug. Dieses Baumdiagramm entspricht dem Baumdiagramm aus „Ziehen ohne Zurücklegen“ mit dem Unterschied, dass jetzt die erste gezogene Kugel nicht in die Urne zurückgelegt wird, wir sprechen von „Ziehen ohne Zurücklegen“. Im ersten Zug bleibt alles wie es war, jedoch verändern sich jetzt die Wahrscheinlichkeiten an den Ästen des zweiten Zuges. Da die zuerst gezogene Kugel ja nicht zurückgelegt wird, befinden sich für den zweiten Zug ja nur noch 14 Kugeln in der Urne. Wurde zuerst eine rote Kugel gezogen, befinden sich nur noch 5 rote Kugeln in der Urne, jedoch weiterhin 4 gelbe und 5 schwarze. Analog gilt dies für das Ziehen einer gelben oder schwarzen Kugel im ersten Zug. |
1. Pfadregel
| In einem Baumdiagramm gibt es zwei Regeln: Wandert man eine Pfad entlang vom Startpunkt bis zum Ausgang, so werden die Wahrscheinlichkeiten an den Ästen multipliziert. Werden also zwei rote Kugeln gezogen, so ist die Wahrscheinlichkeit für zwei rote Kugeln 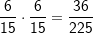 , für zwei gelbe Kugeln , für zwei gelbe Kugeln 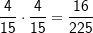 und für zwei schwarze Kugeln und für zwei schwarze Kugeln 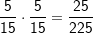 . Analog gilt dies auch für alle anderen Farbkombinationen. . Analog gilt dies auch für alle anderen Farbkombinationen. |
2. Pfadregel
| In einem Baumdiagramm gibt es zwei Regeln: Liegen die Wahrscheinlichkeiten für ein Elementarereignis fest (jeder einzelne Ausgang des Baumdiagramms wird als Elementarereignis bezeichnet), werden die Einzelwahrscheinlichkeiten zur Gesamtwahr-scheinlichkeit addiert. Wird z.B. nach dem Ereignis „zwei rote Kugeln“ gefragt, so gibt es nur einen einzigen Ausgang, nämlich den mit 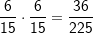 bei „mit Zurücklegen“ bzw. bei „mit Zurücklegen“ bzw. 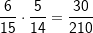 bei „ohne Zurücklegen“. bei „ohne Zurücklegen“.Es könnte ja aber auch nach dem Ereignis „eine rote und eine gelbe Kugel“ gefragt sein. Wenn du nun das Baumdiagramm „Ziehen mit Zurücklegen“ betrachtest, so kommt das Ereignis „eine rote Kugel und eine gelbe Kugel“ ja zweimal vor, nämlich der Ausgang „rg“ und der Ausgang „gr“. Und jetzt besagt die zweite Pfadregel, dass du die Einzelwahrscheinlichkeiten für „rg“ und „gr“ addieren musst, was zu 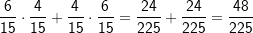 bei „mit Zurücklegen“ bzw. bei „mit Zurücklegen“ bzw. 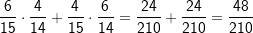 bei „ohne Zurücklegen“ führt. bei „ohne Zurücklegen“ führt.Oder du sollst die Wahrscheinlichkeit für zwei gleichfarbige Kugeln ermitteln. Zwei gleichfarbige Kugeln können sein „rr“, „gg“, „ss“. Somit musst du addieren, nämlich 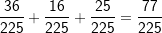 bei „mit Zurücklegen“. bei „mit Zurücklegen“. |
3. Das Gegenereignis
| Zum „Gegenereignis“ greifen wir immer dann, wenn in einer Aufgaben-stellung die Begriffe „mindestens“ oder „höchstens“ vorkommen. Wir bleiben bei unserem Beispiel von oben mit den 6 roten, 4 gelben und 5 schwarzen Kugeln. Das Ereignis lautet nun „mindestens eine rote Kugel“. Mindestens eine rote Kugel bedeutet aber eine oder gar zwei rote Kugeln. Jetzt können wir zwar an Hand des Baumdiagramms gemäß der zweiten Pfadregel die Wahr-scheinlichkeiten aller der Elementarereignisse addieren, in denen eine oder zwei rote Kugeln auftreten. Das wären dann die Ereignisse „rr“, „rg“, „rs“, „gr“ und „sr“, also (beim Ziehen mit Zurücklegen): 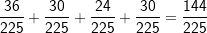 , ein nicht unerheblicher Rechenaufwand also. , ein nicht unerheblicher Rechenaufwand also.Wir können aber auch das Gegenereignis definieren. Das Gegenereignis von „mindestens eine rote Kugel“ ist „keine rote Kugel“. Da jedoch die Summe aller Elementarereignisse 1 ergeben muss, kann das Ereignis P(mindestens eine rote Kugel)=1-P(keine rote Kugel) beschrieben werden. P(keine rote Kugel) kommt im Baumdiagramm jedoch nur als „gg“, „gs“, „sg“ und „ss“ vor. Somit ist: P(mindestens eine rote Kugel)= 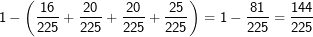 . .Das Ereignis lautet nun „höchstens eine rote Kugel“. Höchstens eine rote Kugel bedeutet aber eine oder keine rote Kugel. Jetzt können wir zwar an Hand des Baumdiagramms gemäß der zweiten Pfadregel die Wahrscheinlichkeiten aller der Elementarereignisse addieren, in denen eine oder keine rote Kugel auftritt. Das wären dann die Ereignisse „rg“, „rs“, „gr“, „gg“, „gs“, „sr“, „sg“ und „ss“, also (beim Ziehen mit Zurücklegen): 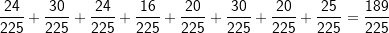 , ebenfalls nicht unerheblicher Rechenaufwand. , ebenfalls nicht unerheblicher Rechenaufwand.Wir können aber auch hier das Gegenereignis definieren. Das Gegenereignis von „höchstens eine rote Kugel“ ist „zwei rote Kugeln“. Da jedoch die Summe aller Elementarereignisse 1 ergeben muss, kann das Ereignis über P(höchstens eine rote Kugel)=1-P(zwei rote Kugeln) dargestellt werden. P(zwei rote Kugeln) kommt im Baumdiagramm jedoch nur als „rr“ vor. Somit ist: P(höchstens eine rote Kugel)= 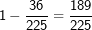 bei „Ziehen mit Zurücklegen“. bei „Ziehen mit Zurücklegen“. |
4. Reduzierte Baumdiagramme
| Es genügt, ein reduziertes Baumdiagramm zu erstellen, wenn nicht alle Ereignisse eines Zufallsexperiments dargestellt werden müssen/sollen. Betrachten wir uns hierzu nochmal das o.a. Ereignis E: „mindestens eine rote Kugel“. Selbst mit dem Gegenereignis F: „keine rote Kugel“ mussten wir insgesamt vier Einzelereignisse ermitteln gegenüber fünf, wenn wir nicht über das Gegenereignis berechnet hätten. Der Rechenaufwand hat sich also nicht wesentlich vermindert. Wir erstellen für diesen Fall somit ein reduziertes Baumdiagramm, was folgendermaßen aussieht: |
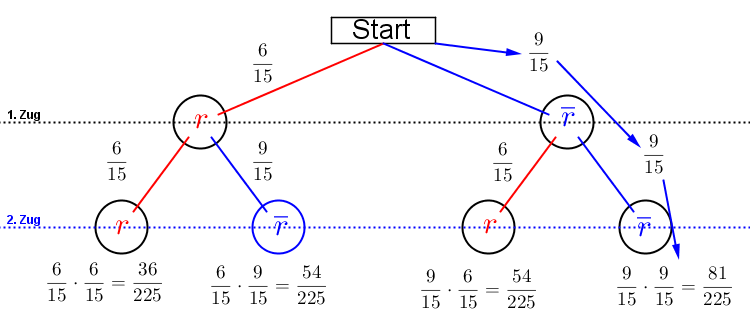 |
In diesem reduzierten Baumdiagramm haben wir einfach die gelben und schwarzen Kugeln zusammengezählt und gesagt, das sind die „nicht roten“ Kugeln. Davon haben wir ja insgesamt neun Stück. Jetzt sind wir in der Lage, das Gegenereignis F: „keine rote Kugel“ sehr schnell zu errechnen, aus dem Baumdiagramm lesen wir ab P(keine rote Kugel)=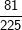 und damit ist das Ereignis P(mindestens eine rote Kugel)= und damit ist das Ereignis P(mindestens eine rote Kugel)=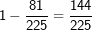 . . |
5. Tabellarische Ermittlung der Wahrscheinlichkeit
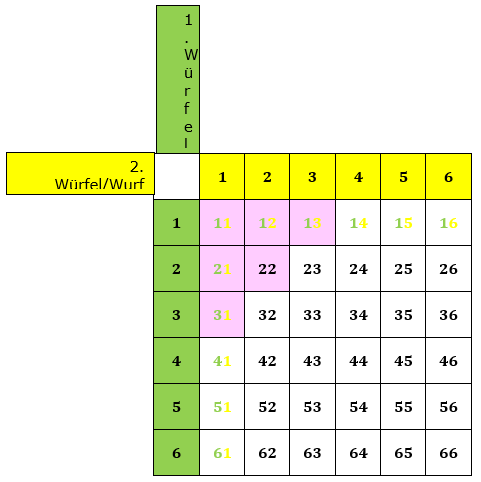
| Baumdiagramme haben die Eigenschaft, dass sie sehr schnell unübersichtlich werden. Bei bis zu drei unterschiedlichen Ästen (rote, gelbe, schwarze Kugel) geht es ja noch. Werden es aber mehr Äste, wie z.B. beim Würfeln, haben wir im 1. Wurf bereits sechs Äste, die sich beim zweiten Wurf an jedem der Äste wiederum um sechs Äste verzweigen. Beim zweistufigen Zufallsexperiment bekommen wir also insgesamt 36 Ausgänge und müssten 36 Rechenoperationen durchführen, um die Wahrscheinlichkeit jedes Elementarereignisses zu ermitteln. In solchen Fällen ist es günstiger, sich einer Tabelle zu bedienen, wie die nachfolgende Grafik beweist. Wir führen ein Zufallsexperiment aus, in dem ein Würfel zweimal geworfen wird und wir möchten feststellen, mit welcher Wahrscheinlichkeit die Augensumme kleiner ist als 5. |
||||||||
 |
||||||||
Die senkrechte (grüne) und waagrechte (gelbe) Spalte stehen jeweils für eine Würfelzahl. Im 6X6-Gitter stehen dann die einzelnen Kombinationen, die durch zweimaliges Würfeln eines Würfels bzw. einmaliges Würfeln mit zwei Würfeln entstehen können. Nun ist die Wahrscheinlichkeit, mit einem Würfel eine Augenzahl zu werfen ja für alle 6 Würfelseiten dieselbe, also 1/6. Wird nun zweimal geworfen, so gilt nach der 1. Pfadregel für jede Kombination die Wahrscheinlichkeit 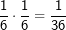 . Somit hat jedes einzelne Ereignis aus obiger Tabelle die Wahrscheinlichkeit . Somit hat jedes einzelne Ereignis aus obiger Tabelle die Wahrscheinlichkeit 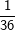 . .Mit dieser grundsätzlichen Überlegung wenden wir uns nun der Lösung der Aufgabe zu:
|
||||||||
6. Der Erwartungswert
| Der Erwartungswert bei der Wahrscheinlichkeitsrechnung ist nichts anderes als das arithmetische Mittel aus der Anzahl der Elementarereignisse multipliziert mit ihrer Wahrscheinlichkeit. Allerdings muss nun das Elementarereignis eine Zahl sein. Mit dem Elementarereignis „zwei rote Kugeln“ lässt sich kein Erwartungswert berechnen. Wir machen uns dies am Beispiel mit dem zweimaligen Werfen eines Würfels und der daraus entstehenden Augensumme klar. Die Augensumme als Elementarereignis ist ja eine Zahl. Wenn du einen Erwartungswert ermitteln sollst, fertigst du bitte sofort eine Tabelle an. Die Anzahl der Zeilen ist dabei stets 4. Die Anzahl der Spalten richtet sich nach der Anzahl der Elementarereignisse plus 1. In unserem Beispiel mit den Würfel können ja die Augensummen von 2 bis 12 auftreten. Das sind also insgesamt 11 Elementarereignisse. Die Tabelle hat also 4 Zeilen und 12 Spalten. Zunächst stellen wir einmal zusammen, wie häufig jedes Elementarereignis vorkommt und erhalten:
In der Zeile xi haben wir die Elementarereignisse eingetragen. In der Zeile P(xi) die Wahrscheinlichkeit des jeweiligen Elementarereignisse. In der Zeile xi⋅P(xi) wurde spaltengerecht das Elementarereignis xi mit seiner Wahrscheinlichkeit P(xi) multipliziert. In der Zeile 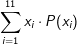 wurden dann die Ergebnisse der Zeile xi⋅P(xi) addiert. Das Resultat dieser Addition ist dann der Erwartungswert E(X). wurden dann die Ergebnisse der Zeile xi⋅P(xi) addiert. Das Resultat dieser Addition ist dann der Erwartungswert E(X).Erwartungswertaufgaben kommen in der Regel bei „Spielaufgaben“ vor. Man errechnet mit E(X) den Verlust bzw. den Gewinn eines Spielers bzw. eines Spielebetreibers. Ist der Erwartungswert bei einem Spiel E(X)=0, so wird das Spiel als "fair" bezeichnet. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |

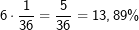 .
.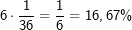 . Dann ist das Ereignis
. Dann ist das Ereignis 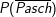 das Gegenereignis zu P(Pasch) und somit
das Gegenereignis zu P(Pasch) und somit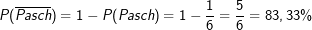 .
.