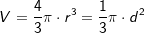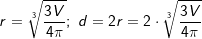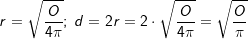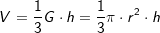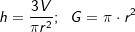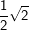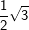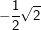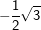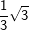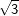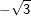|
Zusammengesetzte Körper Realschulabschluss |
Zusammengesetzte Körper Realschulabschluss | Themenerläuterung
aaa(linke Maustaste zum Schließen/Öffnen)
| Im Kapitel Zusammengesetzte Körper Realschulabschluss geht es um die Berechnung von Volumen und Oberfläche von zusammengesetzten Körpern aus z.B. Würfeln, Quadern, Pyramiden, Kegeln, Halbkugeln usw. Es kommen auch Aufgaben vor, bei denen ein Körper aus einem anderen Körper „ausgebohrt“, „ausgearbeitet“ wurde. Bei diesen Aufgaben ist es wichtig zu erkennen, ob die Volumen der einzelnen Körper addiert oder subtrahiert werden müssen, bzw. welche Oberflächen „verdeckt“ sind bzw. „nicht vorhanden“ und damit nicht mehr zur gesamten Oberfläche gehören. Einige Aufgaben sind auch mit der sogenannten „Formvariablen e“ gestellt. |
Die wichtigsten benötigten Formeln
....(linke Maustaste zum Schließen/Öffnen)
1. Der Satz des Pythagoras
| Ist im rechtwinkligen Dreieck c die Hypothenuse (= längste Seite) und a und b die beiden Katheten, so gilt: |
c2=a2+b2 bzw. 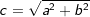 |
a2=c2-b2 bzw. 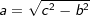 |
b2=c2-a2 bzw. 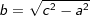 |
2. Die trigonometrischen Formeln
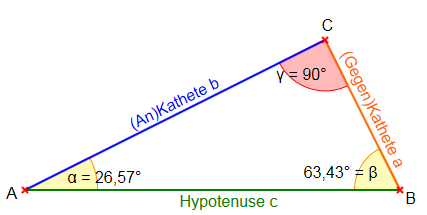 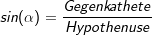 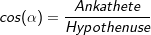 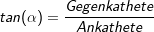 Die Hypothenuse ist immer die längste Seite im rechtwinkligen Dreieck und liegt dem rechten Winkel gegenüber. Die Gegenkathete ist die Kathete, die dem Winkel, um den es geht, gegenüber liegt. Die Ankathete ist die Kathete, die an dem Winkel, um den es geht, anliegt. |
3. Quadrat und Würfel
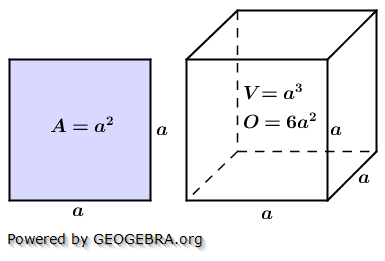 Sei a die Seitenkante, dann gilt: Sei a die Seitenkante, dann gilt: Fläche des Quadrates: A=a2; 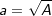 Volumen des Würfels: V=a3; 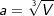 Oberfläche des Würfels: O=6∙a2; 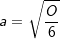 |
4. Rechteck und Quader
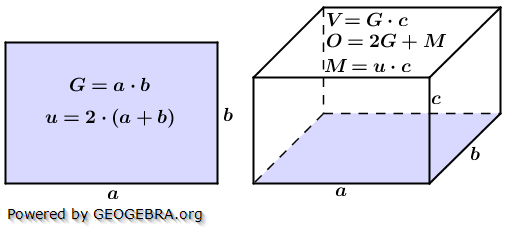 Seien a und b die Seitenkante der rechteckigen Grundfläche und c die Höhe des Quaders, dann gilt: Seien a und b die Seitenkante der rechteckigen Grundfläche und c die Höhe des Quaders, dann gilt:Grundfläche des Quaders: G=a⋅b Volumen des Quaders: V=G⋅c=a∙b∙c Oberfläche des Quaders: O=2∙G+M Mantelfläche des Quaders: M=u∙c mit u=2⋅ (a+b); (u = Umfang der Grundfläche) |
5. Prisma
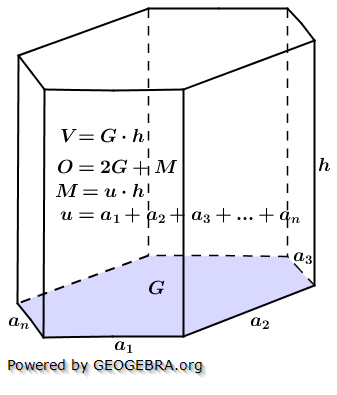 Sei G die Grundfläche eines Prismas und h dessen Höhe, so gilt: Sei G die Grundfläche eines Prismas und h dessen Höhe, so gilt:Volumen des Prismas: V=G⋅h; h=V/G; G=V/h Oberfläche des Prismas: O=2∙G+M Mantelfläche des Prismas: M=u⋅h mit (u = Umfang der Grundfläche) |
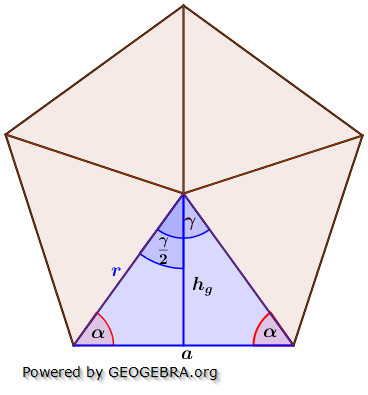
6. Regelmäßige n-Eck-Pyramide
Sei G die Grundfläche einer Pyramide h deren Höhe und n die Anzahl der Ecken der Grundfläche, so gilt:
Diese Formeln gelten auch für Dreieck-, quadratische und Sechseck-Pyramiden. |
  |
||||||||||||||||||||||||||
8. Kreiskegel
 Sei G die Grundfläche eines Kreiskegels und h dessen Höhe, so gilt: Sei G die Grundfläche eines Kreiskegels und h dessen Höhe, so gilt:
|
||||||||||||||||
9. Besondere Werte für sin, cos und tan
Einige Aufgaben sind in Abhängigkeit einer sogenannten „Formvariablen“ gestellt. Diese Formvariable wird mit dem Buchstaben "e" bezeichnet. In diesen Aufgaben wird verlangt, dass du den Nachweis ohne gerundete Werte führen sollst. Dies bedeutet für dich, dass du keinen Taschenrechner verwenden kannst und die Aufgabe manuell lösen musst. In diesen Aufgaben handelt es sich stets nur um Winkel der Größe 30°, 45°, 60° bzw. 90°. Für diese Winkelgrößen gibt es besondere Werte, die in nachstehender Tabelle aufgeführt sind. Diese Tabelle findest du auch in deiner Formelsammlung.
|
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |

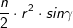 bzw.
bzw.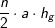
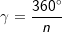 und
und 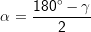
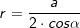 und
und 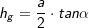
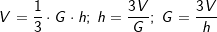
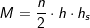
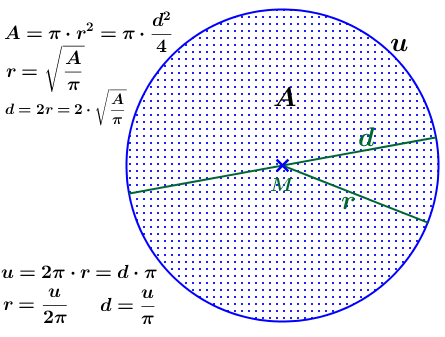 Für die Fläche A eines Kreises mit Radius r und Durchmesser d gilt:
Für die Fläche A eines Kreises mit Radius r und Durchmesser d gilt:
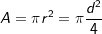
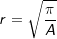
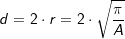
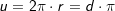
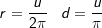
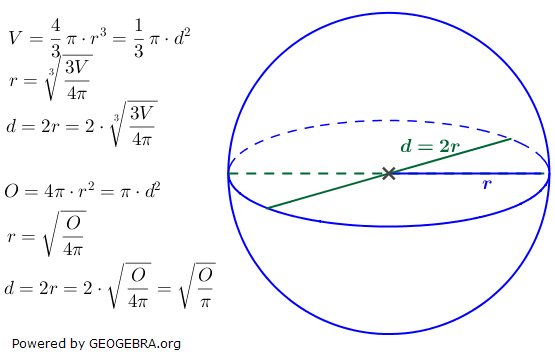 Für eine Kugel mit Radius r und Durchmesser d gilt:
Für eine Kugel mit Radius r und Durchmesser d gilt: