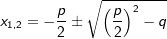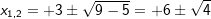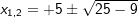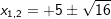|
Gerade und Parabel Realschulabschluss |

Realschulabschluss Gerade und Parabel | Themenerläuterung
aaa(linke Maustaste zum Schließen/Öffnen)
| In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene Punkte aufstellt, was es bedeutet, wenn von Parallelen Geraden die Rede ist, du musst die allgemeine Gleichung einer Parabel in die Scheitelpunktform bringen können und wie man aus der Scheitelpunktgleichung wieder die allgemeine Gleichung berechnet. Weiterhin ist nach den Schnittpunkten von Geraden und Parabeln mit den Koordinatenachsen gefragt bzw. von Schnittpunkten von zwei Parabeln untereinander oder von Schnittpunkten einer Parabel mit einer Geraden. Du solltest weiterhin wissen, wie man eine vorgegebene Parabel an eine andere Stelle im Koordinatensystem verschiebt und wie man durch die Aufgabenstellung wieder auf die neue Parabelgleichung kommt. |
Die wichtigsten benötigten Formeln
....(linke Maustaste zum Schließen/Öffnen)
2. Äquivalenzumformungen
| Es werden alle Rechenoperationen der Äquivalenzumformung von Gleichungen verlangt. |
3. Binomische Formeln
| Die Auflösung der drei binomischen Formeln (a+b)2=a2+2ab+b2, (a-b)2=a2-2ab+b2 sowie (a+b)∙(a-b)=a2-b2 muss bekannt sein. |
4. Aufstellung einer Geradengleichung durch zwei vorgegebene Punkte
Bestimme zunächst die Steigung der Geraden durch die zwei Punkte P1(x1|y1) und P2(x2|y2) mit 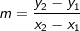 . .Die allgemeine Gleichung der Geraden lautet y=mx+b. Nachdem du m bestimmt hast, machst du eine Punktprobe mit einem der beiden vorgegebenen Punkte, damit kannst du dann b ausrechnen, z. Bsp.
|
||||||
5. Parallele Geraden
| Geraden sind dann parallel zueinander, wenn die beiden Steigungen m1 und m2 den gleichen Wert haben. Die Steigung ist immer die Zahl, die vor dem x in der Gleichung steht. Beispiel: |
 |
| Beide Geraden haben die Steigung 2, also sind sie parallel zueinander. |
6. Parallelverschiebung von Geraden
| Gegeben ist eine Gerade, z. Bsp. y=0,5x-1. Du sollst die Gleichung einer parallelen Geraden durch den Punkt P(2|5) aufstellen. Schreibe zunächst: y=0,5x+b und mache dann mit dem Punkt P die Punktprobe 5=0,5⋅2+b. Hieraus kannst du b ausrechnen mit b=4. Die parallele Gerade hat somit die Gleichung y=0,5x+4. |
7. Die allgemeine Gleichung der Parabel
| Sie lautet y=ax2+bx+c. In 99 % aller Prüfungsaufgaben ist a=1 bzw. a=-1. Da der Mathematiker 1⋅x2 bzw. -1⋅x2 nicht schreibt, findest du nur die Schreibweise x2 bzw. -x2. In all diesen Fällen handelt es sich um einer Normalparabel. Wenn du eine Normalparabel in ein Koordinatensystem einzeichnen sollst, benötigst du keine Wertetabelle, für das Einzeichnen genügt deine Schablone. Findest du nur x2, so ist die Normalparabel nach oben geöffnet. Findest du hingegen -x2, so ist die Normalparabel nach unten geöffnet. Für die wenigen Fälle, in denen a nicht gleich 1 oder -1 ist, musst du wissen: Liegt a zwischen 0 und 1, ist die Parabel nach oben geöffnet und ist breiter. Liegt a zwischen -1 und 0, ist die Parabel nach unten geöffnet und ist breiter. Ist a größer als 1, ist die Parabel nach oben geöffnet und ist schmäler. Ist a kleiner als -1, ist die Parabel nach unten geöffnet und ist schmäler. |
8. Die Scheitelpunktgleichung der Parabel
| Sie lautet y=(x-xs )2+ys, wobei xs für die x–Koordinate und ys für die y–Koordinate des Scheitelpunkts steht. Der Scheitelpunkt ist immer der tiefste Punkt einer nach oben geöffneten, bzw. der höchste Punkt einer nach unten geöffneten Parabel. Bei der x–Koordinate ist besondere Vorsicht geboten. Liest man diese aus der Scheitelpunktgleichung ab (xs) und es steht ein Minus vor der Zahl, so ist die x–Koordinate des Scheitels positiv. Steht hingegen ein Plus vor der Zahl, so ist die x–Koordinate des Scheitels negativ. Beispiel: Die Parabel mit der Gleichung y=(x-3)2+1 hat den Scheitel S(3|1). Die Parabel mit der Gleichung y=-(x+1)2-2 hat den Scheitel S(-1|-2) und ist zusätzlich, wegen des - vor (x+1)2 nach unten geöffnet. |
9. Umformen der Scheitelpunktgleichung in die allgemeine Form
| Aufstellen der allgemeinen Form der Parabelgleichung aus der Scheitelpunktgleichung: Du musst das Binom auflösen und die entstehenden beiden Zahlen zusammenfassen. Beispiel:
|
10. Umformen der allgemeinen Form in die Scheitelpunktgleichung
| Aufstellen der Scheitelpunktgleichung aus der allgemeinen Form. Die allgemeine Form ist über die quadratische Ergänzung in die Scheitelpunktform zu bringen. 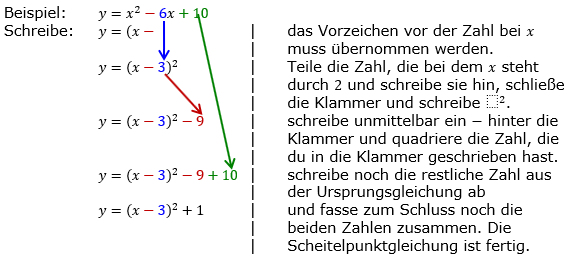 |
11. Schnittpunktbestimmung mit der x-Achse (Nullstellen)
| Setze y=0 und Gerade: Löse die Gleichung durch Äquivalenzumformung nach x auf.
Löse die Gleichung mit der Mitternachtsformel nach x auf.
|
||||||||||||||||||||||||||||||||||||||||||||
12. Schnittpunktbestimmung mit der y-Achse
| Setze x=0 Gerade und Parabel: Löse die Gleichung durch Äquivalenzumformung nach y auf. Beispiel Gerade:
|
||||||||||||||||||||||||||||||||||||
13. Schnittpunktbestimmung Gerade/Parabel bzw. Parabel/Parabel
| Schnittpunktbestimmung erfolgt über Gleichsetzung. Beispiel Gerade/Parabel.
Berechnung derselben durch Einsetzen der beiden x–Werte in eine der Ausgangsgleichungen.
|
||||||||||||||||||||||||||||||||||||||||||||
14. Verschiebung einer Parabel in x-Richtung und y-Richtung
| Bei gegebener Scheitelpunktgleichung der Parabel: Berechne den neuen Scheitelpunkt und ändere die Werte in der Scheitelpunktgleichung auf den neuen Scheitelpunkt ab. Beispiel:S(-1|1-2)
Stelle die allgemeine Form zunächst um in die Scheitelpunktform und verfahre dann wie im Beispiel zuvor. Beispiel:
|
||||||||||||||||||||||||||||||||||||||||
| Aufgaben nach Aufgabengebiet Übungen / Pflicht- / Wahlteile |