|
2010 Abituraufgaben allg. Gymnasium Wahlteil Analytische Geometrie |
Aufgaben des Prüfungsjahres 2010 BW |
| Dokument mit 3 Aufgaben |
Aufgabe B1
| Gegeben sind die Punkte A(0|4|0), B(0|0|2) und C(4|0|0). | |
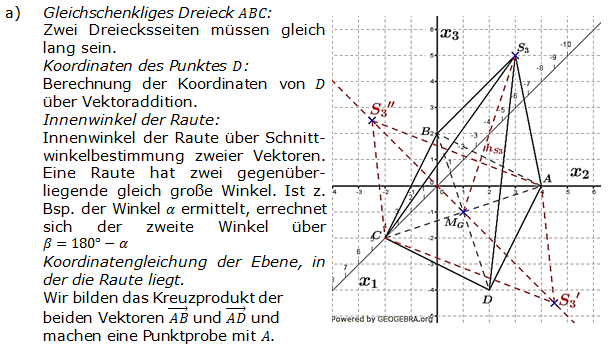
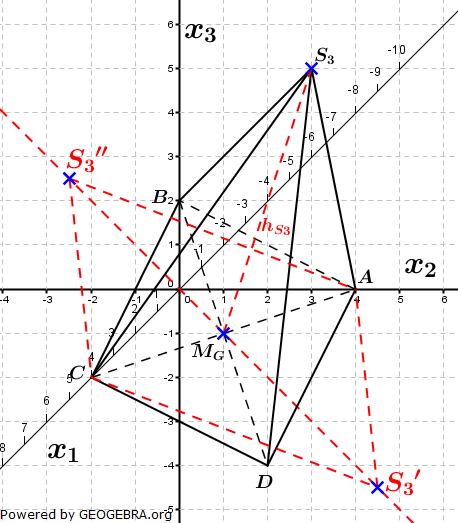
| a) | Zeigen Sie, dass das Dreieck ABC gleichschenklig ist. Ergänzen Sie das Dreieck ABC durch einen Punkt D zu einer Raute. Berechnen Sie die Innenwinkel der Raute. Zeigen Sie, dass die Raute in der Ebene E: x1+x2+2x3=4 liegt. (Teilergebnis: D(4|4|-2)) |
| Gegeben ist für jedes t≠0 der Punkt St(-3+3t|-3+3t|5+t). Die Pyramide Pt hat die Grundfläche ABCD und die Spitze St. | |
| b) | Zeichnen Sie die Pyramide P3 in ein Koordinatensystem. Die Punkte B, D und S3 legen eine Ebene F fest. Bestimmen Sie eine Koordinatengleichung von F. Zeigen Sie, dass die Ebene F Symmetrieebene der Pyramide P3 ist. |
| c) | Für welchen Wert von t geht die Höhe der Pyramide Pt durch den Mittelpunkt der Grundfläche? Das gleichschenklige Dreieck ACS3 wird um die Achse AC gedreht. In welchen Punkten durchstößt dabei seine Spitze die x1x2-Ebene? |
| |
Aufgabe B2.1
Gegeben sind der Punkt A(4,5|6|3,5) spwie die Gerade 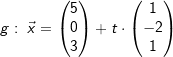 . . |
|
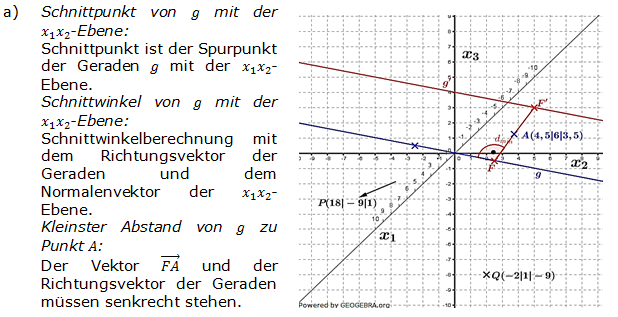
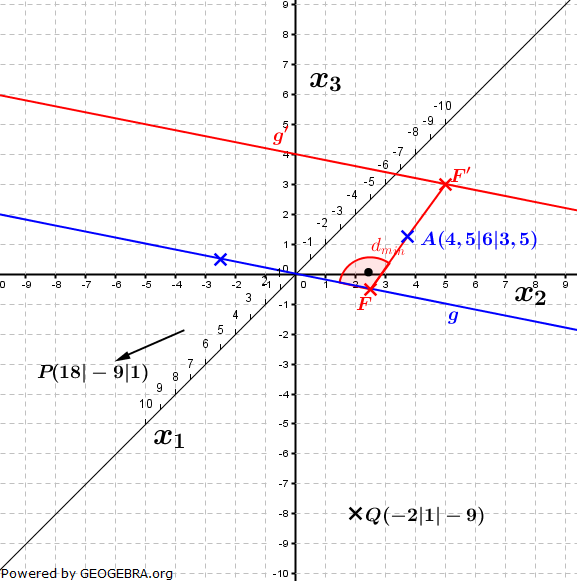
| a) | Bestimmen Sie den Schnittpunkt der Geraden g mit der x1x2-Ebene. Zeichnen Sie die Gerade g in ein Koordinatensystem. Unter welchem Winkel schneidet g die x1x2-Ebene? Welcher Punkt F auf der Geraden g hat vom Punkt A den kleinsten Abstand? Die Gerade h entsteht durch Spiegelung von g an A. Bestimmen Sie eine Gleichung der Geraden h. (Teilergebnis: F(3|4|1)) |
| b) | Begründen Sie, dass bei Rotation der Geraden g um die Gerade durch A und F eine Ebene entsteht. Zeigen Sie, dass 3x1+4x2+5x3=30 eine Gleichung dieser Ebene ist. Untersuchen Sie, ob die Punkte P(18|-9|1) und Q(-2|1|-9) auf verschiedenen Seiten dieser Ebene liegen. |
| |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 17. Juli 2019 17. Juli 2019








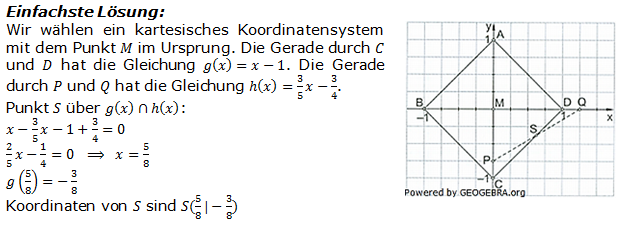
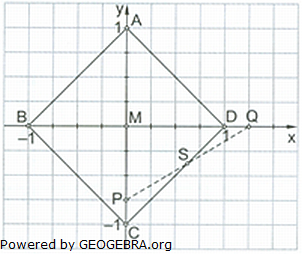
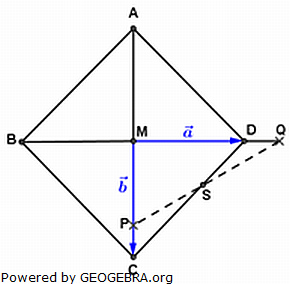
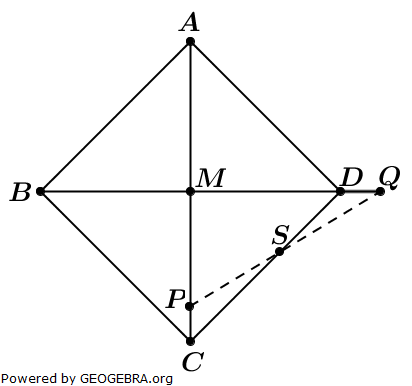 Das Quadrat ABCD hat den Mittelpunkt M. Die Punkte P und Q werden so gewählt, dass
Das Quadrat ABCD hat den Mittelpunkt M. Die Punkte P und Q werden so gewählt, dass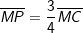 und
und 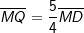 gilt.
gilt.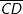 und
und 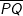 schneiden sich im Punkt S.
schneiden sich im Punkt S.