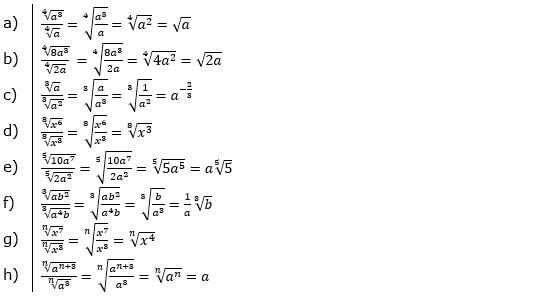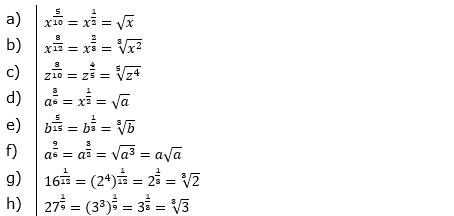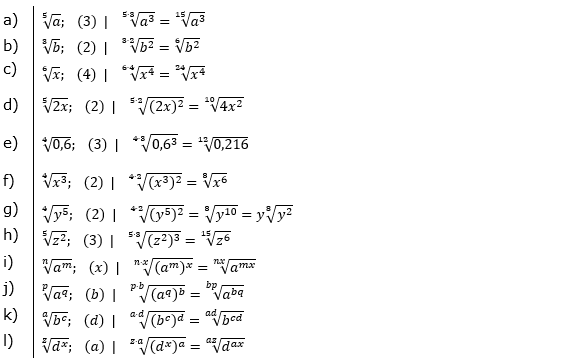|
Vermischte Aufgaben mit Wurzeln - Aufgabenblatt 4 |
| Dokument mit 37 Aufgaben |
Aufgabe A1 (8Teilaufgaben)
| Vereinfache. | |||
| a) | 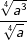 |
= | _______________________ |
| b) | 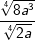 |
= | _______________________ |
| c) | 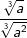 |
= | _______________________ |
| d) | 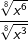 |
= | _______________________ |
| e) | 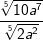 |
= | _______________________ |
| f) | 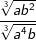 |
= | _______________________ |
| g) | 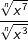 |
= | _______________________ |
| h) | 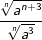 |
= | _______________________ |
| |
Aufgabe A2 (8 Teilaufgaben)
| Kürze die Exponenten und stelle den Term in Wurzeldarstellung auf. | |||
| a) | 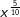 |
= | _______________________ |
| b) | 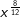 |
= | _______________________ |
| c) | 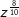 |
= | _______________________ |
| d) | 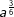 |
= | _______________________ |
| e) | 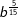 |
= | _______________________ |
| f) | 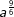 |
= | _______________________ |
| g) | 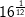 |
= | _______________________ |
| h) | 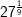 |
= | _______________________ |
| |
Aufgabe A3 (12 Teilaufgaben)
| Erweitere die Exponenten mit der angegebenen Zahl. | |||
| a) | 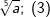 |
= | _______________________ |
| b) | 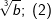 |
= | _______________________ |
| c) | 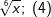 |
= | _______________________ |
| d) | 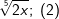 |
= | _______________________ |
| e) | 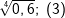 |
= | _______________________ |
| f) | 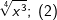 |
= | _______________________ |
| g) | 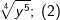 |
= | _______________________ |
| h) | 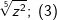 |
= | _______________________ |
| i) | 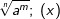 |
= | _______________________ |
| j) | 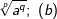 |
= | _______________________ |
| k) | 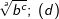 |
= | _______________________ |
| l) | 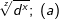 |
= | _______________________ |
| |
Aufgabe A4 (9 Teilaufgaben)
| Bringe auf den gleichen Wurzelexponenten: | |
| Beispiel: | 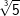 und und 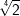 |
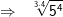 und und 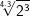 |
|
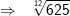 und und 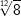 |
|
| a) | 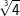 und und 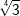 |
= | _______________________ |
| b) | 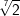 und und 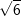 |
= | _______________________ |
| c) | 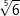 und und 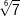 |
= | _______________________ |
| d) | 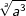 und und 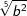 |
= | _______________________ |
| e) | 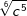 und und 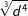 |
= | _______________________ |
| f) | 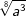 und und 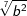 |
= | _______________________ |
| g) | 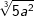 und und 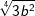 |
= | _______________________ |
| h) | 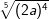 und und 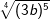 |
= | _______________________ |
| i) | 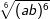 und und 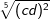 |
= | _______________________ |
| |
| Du befindest dich hier: |
| Vermischte Aufgaben mit Wurzeln - Aufgabenblatt 4 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 15. Juli 2021 15. Juli 2021