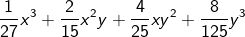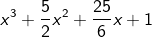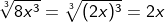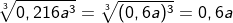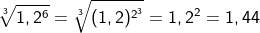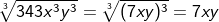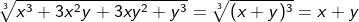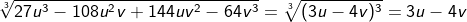| Ziehe, falls möglich, die Kubikwurzel. |
|
Hinweis:
Bisweilen müssen wir den Radikanten, also den unter dem Wurzelzeichen stehenden Term, zunächst in einen Ausdruck der dritten Potenz umwandeln, ehe wir die dritte Wurzel ziehen können, wie die folgenden Beispiele zeigen.
|
|
Wie wir bei den beiden letzten Beispielen gesehen haben, ist die Kenntnis der 1. und 2. binomischen Formel dritten Grades zwingend.
Aber ACHTUNG !!! Nicht jeder viergliedrige Ausdruck lässt sich in ein Binom umwandeln. So kann der Term 27u3+20u2v+14uv2+64v3 nicht in der Form (3u+2b)3 geschrieben werden, denn: |
|
(3u+2b)3=27u3+18u2b+12ub2+8b3 |
|
Also Vorsicht, bei der nächsten Übung. |
| a) |
64a3 |
b) |
1,331x3 |
c) |
512a3b3 |
| d) |
8x3+6x2y+6xy2+y3 |
e) |
126 |
f) |
(-12)6 |
| g) |
-126 |
h) |
-46 |
i) |
64x6 |
| j) |
8(s3-3s2t+3st2-t3) |
k) |
0,027a3-0,054a2b+0,036ab2-0,008b3 |
| l) |
125x3-300x2y-240xy2+64y3 |
| m) |
125x3+50x2y+20xy2+8y3 |
| n) |
 |
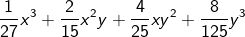o) |
9a3+2a2+4a+16 |
| p) |
27a3-108a2+144a-64 |
q) |
0,125a3+0,75a2+1,5a+1 |
| r) |
s3+t3 |
s) |
(s+t)3 |
| t) |
(s2+t2)3 |
u) |
(s2-t2)3 |
| v) |
a3-a2b+ab2+b3 |
w) |
 |
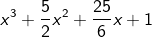| x) |
x3-45x2+675x-3375 |
y) |
a3-27a2+9a-17 |
Eine Frage stellen...
Fehler melden...
