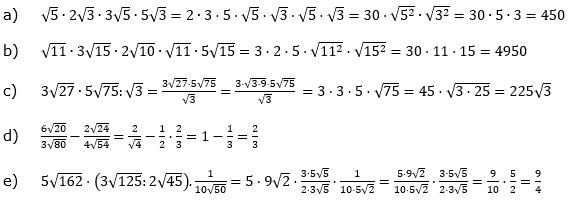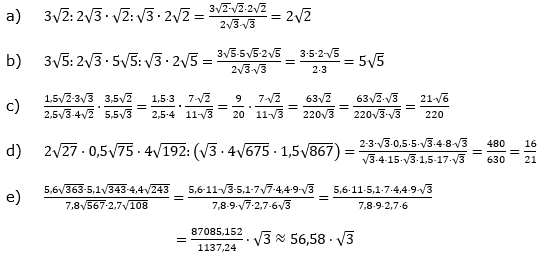 |
Multiplikation und Division von Wurzeln - Level 2 - Fortgeschritten - Blatt 1 |
| Dokument mit 10 Aufgaben |
Aufgabe A1 (5 Teilaufgaben)
| Fasse so weit wie möglich zusammen. | |
| a) |  |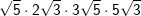
| _______________________________________________________ | |
| b) |  |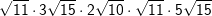
| _______________________________________________________ | |
| c) |  |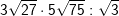
| _______________________________________________________ | |
| d) |  |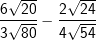
| _______________________________________________________ | |
| e) |  |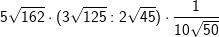
| _______________________________________________________ | |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (5 Teilaufgaben)
| Berechne und bereinfache so weit wie möglich. Manchmal ist es einfacher, vor der Multiplikation / Division teilweise die Wurzel zu ziehen. | |
| a) |  |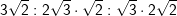
| _______________________________________________________ | |
| b) |  |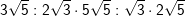
| _______________________________________________________ | |
| c) |  |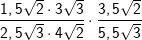
| _______________________________________________________ | |
| d) |  |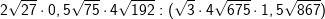
| _______________________________________________________ | |
| e) |  |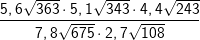
| _______________________________________________________ | |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Multiplikation und Division von Wurzeln Level 2 - Fortgeschritten - Blatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 15. Juli 2021 15. Juli 2021
