|
Vermischte Aufgaben mit Wurzeln - Aufgabenblatt 9 |
| Dokument mit 34 Aufgaben |
Aufgabe A1 (6 Teilaufgaben)
| Vereinfache. | |||
| a) | 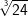 |
= | _______________________ |
| b) | 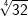 |
= | _______________________ |
| c) | 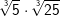 |
= | _______________________ |
| d) | 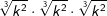 |
= | _______________________ |
| e) | 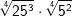 |
= | _______________________ |
| f) | 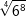 |
= | _______________________ |
| |
Aufgabe A2 (3 Teilaufgaben)
| Mache den Nenner rational. | |||
| a) | 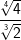 |
= | _______________________ |
| b) | 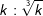 |
= | _______________________ |
| c) | 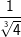 |
= | _______________________ |
| |
Aufgabe A3 (6 Teilaufgaben)
| Schreibe als Potenz. | |||
| a) | 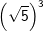 |
= | _______________________ |
| b) | 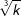 |
= | _______________________ |
| c) | 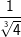 |
= | _______________________ |
| d) | 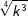 |
= | _______________________ |
| e) | 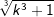 |
= | _______________________ |
| f) | 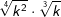 |
= | _______________________ |
| |
Aufgabe A4 (9 Teilaufgaben)
| Vereinfache und schreibe das Ergebnis als Wurzel. | |||
| a) | 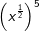 |
= | _______________________ |
| b) | 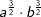 |
= | _______________________ |
| c) | 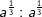 |
= | _______________________ |
| d) | 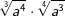 |
= | _______________________ |
| e) | 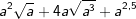 |
= | _______________________ |
| f) | 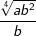 |
= | _______________________ |
| g) | 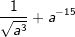 |
= | _______________________ |
| h) | 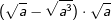 |
= | _______________________ |
| i) | 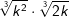 |
= | _______________________ |
| |
Aufgabe A5 (6 Teilaufgaben)
| Vereinfache. | |||
| a) | 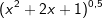 |
= | _______________________ |
| b) | 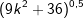 |
= | _______________________ |
| c) | 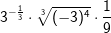 |
= | _______________________ |
| d) | 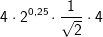 |
= | _______________________ |
| e) | 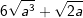 |
= | _______________________ |
| f) | 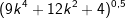 |
= | _______________________ |
| |
Aufgabe A7
| Welche der folgenden Aussagen sind wahr oder falsch? Begründe. | ||
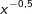 ist ist |
||
| a) für alle x ≥ 0 definiert | b) für alle 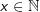 definiert definiert |
c) gleich 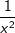 |
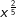 ist ist |
||
a) für alle 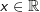 definiert definiert |
b) die 5. Wurzel von x2 | c) die Quadratwurzel von x2 |
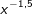 ist ist |
||
a) für alle 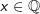 definiert definiert |
b) gleich 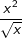 |
c) gleich 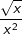 |
| |
| Du befindest dich hier: |
| Vermischte Aufgaben mit Wurzeln - Aufgabenblatt 9 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 15. Juli 2021 15. Juli 2021

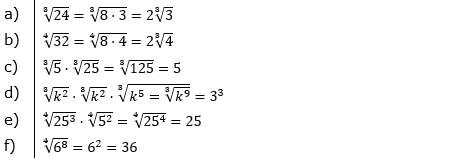
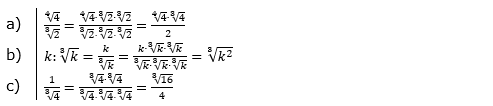
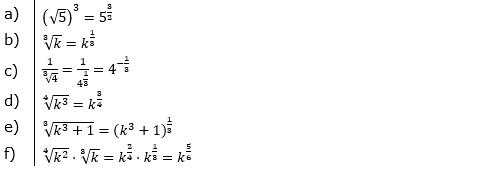
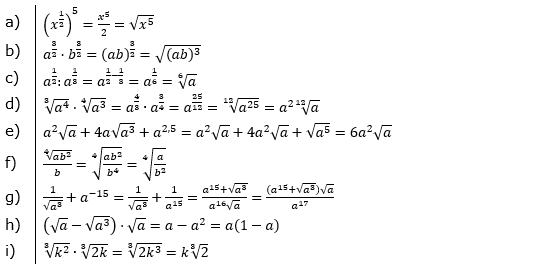
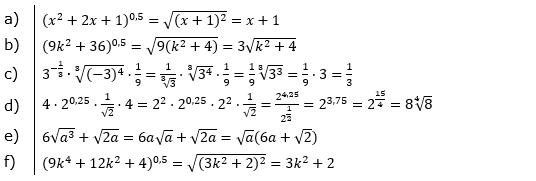
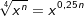 ?
?