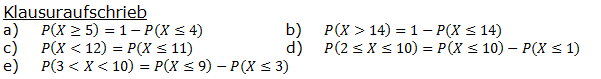 |
Stochastik Binomialverteilung Fortgeschritten - Aufgabenblatt 1 |
| Dokument mit 26 Aufgabe |
Aufgabe A1 (5 Teilaufgaben)
| Stelle die Wahrscheinlichkeiten so um, damit eine Berechnung mit dem GTR bzw. WTR möglich wäre. | |||||
| a) | P(X≥5) | b) | P(X>14) | c) | P(X<12) |
| d) | P(3≤X≤10) | e) | P(3<X<10) | ||
 Eine Frage stellen... |
Fehler melden...
(8 Teilaufgaben)Aufgabe A2 (8 Teilaufgaben)
| Herr Maier muss jeden Morgen auf dem Weg zur Arbeit einen Bahnübergang passieren. Die Schranke ist mit einer Wahrscheinlichkeit von 25 % geschossen. Berechne die Wahrscheinlichkeit, dass Herr Maier innerhalb eines Monats (mit 22 Arbeitstagen) |
|
| a) | genau fünfmal warten muss. |
| b) | höchstens fünfmal warten muss. |
| c) | mindestens achtmal warten muss. |
| d) | weniger als sechsmal warten muss. |
| e) | mehr als zehnmal warten muss. |
| f) | nie warten muss. |
| g) | mindestens fünf und höchstens zwölfmal warten muss. |
| h) | weniger als fünfzehnmal und mehr als sechsmal warten muss. |
| Eine Frage stellen... |
Aufgabe A3 (3 Teilaufgaben)
| In einer Urne befinden sich 12 schwarze und 4 weiße Kugeln. Es werden 12 Kugeln mit Zurücklegen gezogen. Die Zufallsvariable X zählt die Anzahl der schwarzen Kugeln. | |
| a) | Berechne die Wahrscheinlichkeit, dass genau fünf schwarze Kugeln gezogen werden. |
| b) | Berechne μ=E(X) (Erwartungswert von X) und interpretiere diesen Wert. |
| c) | Berechne P(X=μ) und P(μ-1≤X≤μ+1). |
| Eine Frage stellen... |
Aufgabe A4 (3 Teilaufgaben)
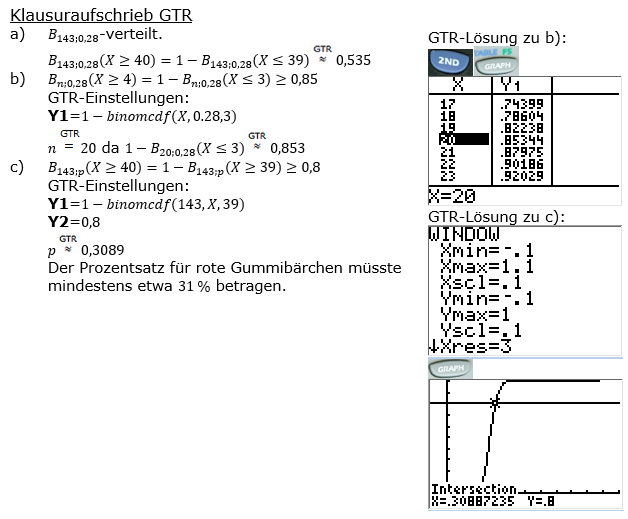
| a) | Ein Hersteller von Gummibärchen produziert 28 % rote Bärchen. Wie groß ist die Wahrscheinlichkeit, dass in einer Tüte mit 143 Gummibärchen mindestens 40 rote sind? |
| b) | Ein Hersteller von Gummibärchen produziert 28 % rote Bärchen. Marlene entnimmt mit geschlossenen Augen aus einem großen Behälter (der sehr viele Gummibärchen enthält) ein Gummibärchen nach dem anderen. Wie viele muss sie entnehmen, damit sie mit mindestens 85 % Wahrscheinlichkeit mindestens vier rote Bärchen bekommt? |
| c) | Ein Hersteller von Gummibärchen verkauft diese in Tüten zu 143 Stück. Wie hoch muss der Anteil der roten Gummibärchen in der Produktion sein, damit in einer Tüte mit einer Wahrscheinlichkeit von mindestens 80 % mindestens 40 Rote sind? |
| Eine Frage stellen... |
Aufgabe A5 (3 Teilaufgaben)
| In einer Vogelkolonie auf einer Nordseeinsel leben 8000 Möwen. Ein Wissenschaftlerteam fängt 100 von ihnen und versieht jeden mit einem Markierungsring. | |
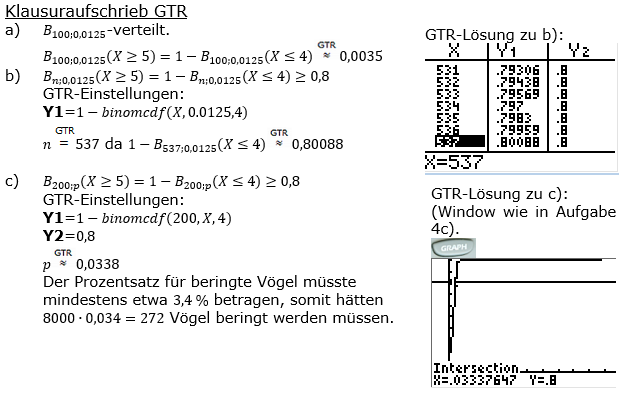
| a) | Ein halbes Jahr später werden wiederum 100 Vögel dieser Kolonie gefangen. Mit welcher Wahrscheinlichkeit haben mindestens fünf von ihnen einen Ring? |
| b) | Wie viele Vögel muss man fangen, um mit mindestens 80 % Wahrscheinlichkeit mindestens fünf mit Ring zu erhalten? |
| c) | Wie viele Vögel hätte das Wissenschaftsteam mit einem Ring versehen müssen, damit unter 200 Vögeln mit mindestens 80 % Wahrscheinlichkeit mindestens fünf mit Ring sind? |
| Eine Frage stellen... |
Aufgabe A6 (4 Teilaufgaben)
| In einem Unternehmen werden Sauerkirschen maschinell entsteint und dann in Gläser abgefüllt. 1,5 % der fertigen Kirschen haben trotzdem noch ihren Kern. | |
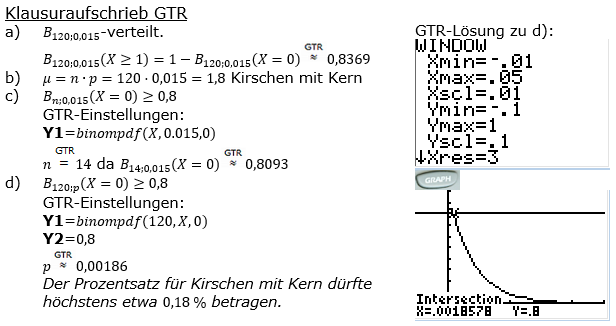
| a) | Herr Becker backt einen Kirschkuchen. Dafür nimmt er 120 dieser Kirschen. Wie groß ist die Wahrscheinlichkeit, dass sich in dem Kuchen mindestens ein Kirschkern befindet? |
| b) | Wie viele Kirschkerne sind in einem solchen Kuchen zu erwarten? |
| c) | Wie viele Kirschen dürfte Herr Becker für seinen Kuchen höchstens nehmen, damit er mit mindestens 80 % Wahrscheinlichkeit keinen Kern darin hat? |
| d) | Wie groß darf die Wahrscheinlichkeit, dass eine Kirsche noch ihren Kern hat, sein, damit sich mit mindestens 80 % Wahrscheinlichkeit in einem Kirschkuchen mit 120 Kirschen kein Kirschkern befindet? |
| Eine Frage stellen... |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 03. November 2024 03. November 2024
