 |
Stochastik Erwartungswert Fortgeschritten - Aufgabenblatt 2 |
| Dokument mit 12 Aufgaben |
| Hinweis Bei Aufgaben zum Erwartungswert empfehlen wir dir, unmittelbar eine Tabelle der xi und P(X=xi) anzulegen. |
(2 Teilaufgaben)Aufgabe A1 (2 Teilaufgaben)
| Bei einer großen Produktionsserie von Speicherchips beträgt der Ausschussanteil 10 %. Chips dieser Serie werden ungeprüft in Packungen zu je 100 Stück verkauft. | ||
| a) | Mit welcher Wahrscheinlichkeit sind in einer Packung höchstens 10 defekte Chips? | |
| b) | Der Kaufpreis für einen Großabnehmer beträgt pro Packung 800 €. Mit dem Abnehmer wird vereinbart, dass eine Packung zurückgegeben und der Kaufpreis erstattet wird, wenn mehr als k defekte Chips in der Packung sind. Für eine solche Rücknahme entstehen der Herstellerfirma Kosten in Höhe von 250 €. Welchen Wert muss k mindestens haben, damit der durchschnittliche Erlös pro Packung mindestens 700 € beträgt? |
|
 Eine Frage stellen... |
Fehler melden...
Aufgabe A2 (2 Teilaufgaben)
| Bei einem Glücksspiel wird ein idealer Würfel viermal geworfen und die Anzahl der Sechsen notiert. Als Auszahlungen sind vorgesehen: |
||
| 0 € | bei höchstens einer Sechs, | |
| 2 € | bei zwei Sechsen, | |
| 10 € | bei drei Sechsen, | |
| 50 € | bei viker Sechsen. | |
| Der Einsatz pro Spiel beträgt 1 €. | ||
| a) | Begründen Sie, dass das Spiel nicht fair ist. | |
| b) | Der Auszahlungsplan soll so geändert werden, dass der Erwartungswert für den Verlust eines Spielers 20 Cent beträgt. Dazu soll auch für den Fall, dass höchstens eine Sechs notiert wird, ein Betrag ausgezahlt werden sowie das 10–fache dieses Betrages bei zwei Sechsen. Die beiden anderen Auszahlungsbeträge bleiben unverändert. Bestimme die geänderten Auszahlungsbeträge. | |
| Eine Frage stellen... |
Aufgabe A3 (2 Teilaufgaben)
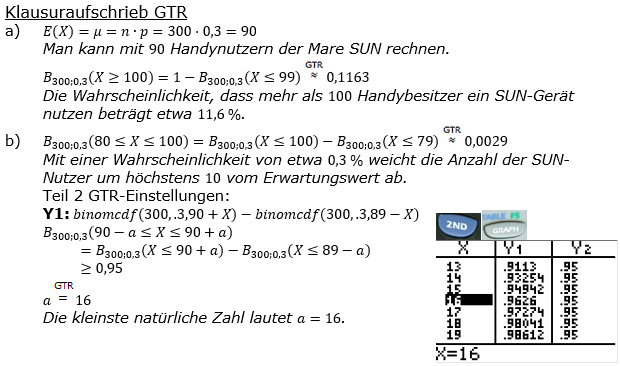
| Aus Umfragen weiß man, dass aller Handybesitzer ein Gerät der Marke SUN verwenden. Es werden zufällig 300 Handybesitzer ausgewählt. Die Zufallsvariable X beschreibt darunter die Anzahl der Handybesitzer, die ein Gerät der Marke SUN nutzen. | ||
| a) | Mit welcher Anzahl von SUN-Nutzern kann man rechnen? Mit welcher Wahrscheinlichkeit nutzen mehr als 100 Handybesitzer ein SUN-Gerät? |
|
| b) | Mit welcher Wahrscheinlichkeit weicht die Anzahl der SUN-Nutzer um höchstens 10 vom Erwartungswert von X ab? Bestimme eine möglichst kleine natürliche Zahl a so, dass die Anzahl der SUN-Nutzer mit mindestens 95 % Wahrscheinlichkeit um höchstens a vom Erwartungswert von X abweicht. |
|
| Eine Frage stellen... |
Aufgabe A4 (2 Teilaufgaben)
| Bei einer Lotterie werden Lose verkauft, auf denen jeweils eine von einem Computer zufällig erzeugte sechsstellige Zahl aufgedruckt ist. Jede dieser Zahlen besteht nur aus den Ziffern 0 und 1, die mit Wahrscheinlichkeiten 0,75 bzw. 0,25 erzeugt werden. Jedes Los, bei dem die aufgedruckte Zahl mehr als dreimal die Ziffer 1 enthält, ist ein Gewinnlos. | ||||||
| a) | Wie groß ist die Wahrscheinlichkeit, ein Gewinnlos zu erhalten? | |||||
| b) | Für Gewinnlose gilt der folgende Auszahlungsplan: | |||||
| Anzahl der Ziffern 1 auf dem Gewinnlos | 4 | 5 | 6 | |||
| Auszahlung in € | 5 | 50 | 500 | |||
| Die Lotteriegesellschaft will pro Los durchschnittlich mindestens 0,50 € verdienen. Wie muss dazu der Preis für ein Los kalkuliert werden? | ||||||
| Eine Frage stellen... |
Aufgabe A5 (2 Teilaufgaben)
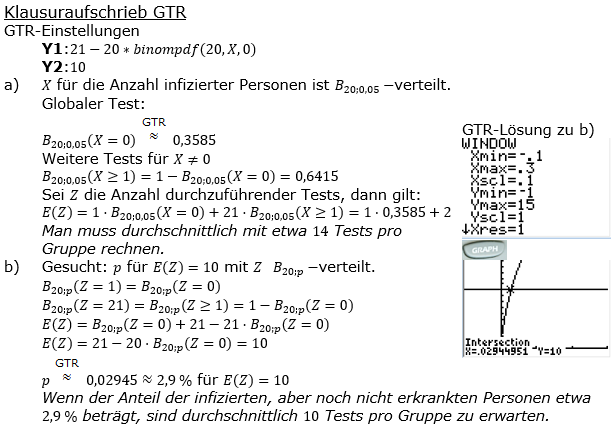
| In einer Bevölkerung ist eine Viruserkrankung ausgebrochen. Der Anteil der infizierten Personen, bei denen die Krankheit aber noch nicht ausgebrochen ist, ist p. Mit einem neu entwickelten Bluttest kann man das Virus sicher nachweisen. Er soll bei einer Reihenuntersuchung eingesetzt werden, um die Krankheit bereits vor Ausbruch zu diagnostizieren. Um die Zahl der teuren Tests möglichst klein zu halten, wird dabei Blut von 20 Personen gemischt und untersucht. Nur wenn sich dabei das Virus nachweisen lässt, wird das Blut jeder der 20 Personen noch einmal einzeln untersucht. | |
| a) | Man geht zunächst von p=0,05 aus. Mit wie vielen Tests muss man durchschnittlich bei Gruppen von 20 Personen rechnen? |
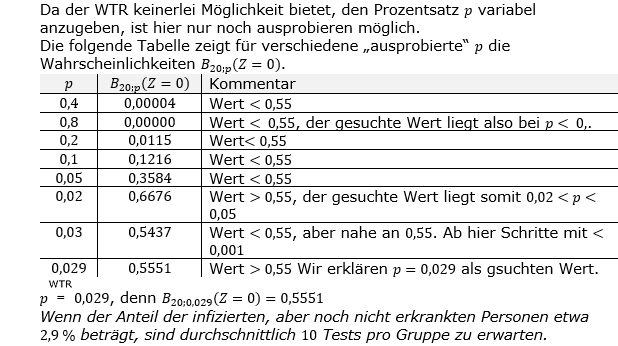
| b) | Für welchen Wert von p sind bei diesem Verfahren durchschnittlich 10 Tests pro Gruppe von 20 Personen zu erwarten? |
| Eine Frage stellen... |
Aufgabe A6 (2 Teilaufgaben)
| Eine Firma produziert elektrische Rasierapparate. Erfahrungsgemäß sind 6 % der produzierten Apparate defekt. Um die defekten Rasierapparate vor dem Verkauf auszusondern, werden alle Geräte überprüft. Bei dieser Überprüfung kommt es bei den defekten Geräten mit der Wahrscheinlichkeit 0,09 und bei den intakten Geräten mit einer Wahrscheinlichkeit von 0,01 zu einer Fehlentscheidung. Alle bei der Überprüfung als intakt deklarierten Geräte werden zum Verkauf freigegeben. | |
| a) | Wie groß ist die Wahrscheinlichkeit, dass es bei der Kontrolle eines Rasierapparats zu einer Fehlentscheidung kommt? |
| b) | Bei wie vielen von 10000 produzierten Rasierapparaten kann man mit einer Verkaufsfreigabe rechnen? Mit welcher Wahrscheinlichkeit weicht die Anzahl der tatsächlich freigegebenen Apparate um höchstens 25 davon ab? |
| Eine Frage stellen... |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 20. Juli 2021 20. Juli 2021
