 |
Kombinatorik in der Stochastik |

1. Einführung
| Die Bezeichnung Kombinatorik geht auf Leibniz zurück. In seiner "Dissertatio de arte combinatoria" aus dem Jahr 1666 beschäftigte er sich mit Permutationen. Historisch entstand die Kombinatorik aus Abzählproblemen von diskreten Strukturen, wie sie im 17. Jahrhundert bei der Wahrscheinlichkeitsanalyse von Glücksspielen auftraten. |
| Dieser klassische Bereich der Kombinatorik wird zusammenfassend als abzählende Kombinatorik (Stichwörter: Variationen und Kombinationen) bezeichnet. Kennzeichnend für die in der abzählenden Kombinatorik auftretenden Probleme war, dass meist für jedes Einzelproblem ad hoc neue Methoden ersonnen werden mussten. Lange Zeit spielte die Kombinatorik deshalb eine Außenseiterrolle in der Mathematik, zusammenfassende Theorien ihrer Teilgebiete entstanden erst im 20. Jahrhundert. |
| Die Kombinatorik hat zahlreiche Anwendungen in anderen Gebieten der Mathematik wie Geometrie, Wahrscheinlichkeitstheorie, Algebra, Mengenlehre und Topologie, in der Informatik (zum Beispiel Kodierungstheorie) und der theoretischen Physik, insbesondere in der statistischen Mechanik sowie in der Unternehmensforschung (zum Beispiel Optimierung, Lagerhaltung). |
2. Zählprinzip von Mengen
In der „Klassischen Wahrscheinlichkeit“ haben wir gesehen, wie sich dieselbe aus der Zahl der günstigen und der möglichen Fälle zu 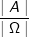 ergibt. ergibt. |
| Bei kleinen Mächtigkeiten |A| und |Ω| helfen Baumdiagramme zur Ermittlung. Spätestens aber, wenn die Baumdiagramme mehrstufig werden und sogar noch aus mehr als drei Elementarereignissen bestehen, ist die Übersichtlichkeit des Baumdiagramms stark eingeschränkt. Stell dir vor, du müsstest |A| und/oder |Ω| für das Lottospiel 6 aus 49 mithilfe eines Baumdiagramms ermitteln. |
| Haben die Ereignisse A und Ω große Mächtigkeiten, lassen sich diese mithilfe der Kombinatorik auf geschickte Weise bestimmen, ohne dass die Elemente, aus denen die Ereignisse bestehen, einzeln notiert und abgezählt werden müssen. Die Grundlage der Kombinatorik in der Sochastik dafür ist das allgemeine Zählprinzip. |
2.1. Beispiel 1
| Horst kombiniert fünf Pullover mit drei Hosen und zwei Paar Schuhen. Gib an, über wie viele verschiedene Outfits Horst damit verfügt. |
| Eine gute Veranschaulichung bietet das Baumdiagramm. |
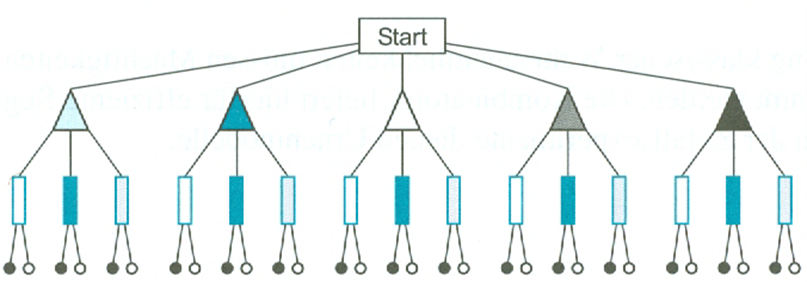 |
| In der Grafik stellen die Dreiecke die verschiedenen Pullover dar, die Rechtecke die Hosen und die Kreise die Schuhe. Wir stellen fest, dass es 5 Möglichkeiten gibt, einen Pullover auszuwählen, 3 Möglichkeiten für die Hosen und 2 Möglichkeiten für die Schuhe. Das Ereignis A: „Outfit“ besteht aus drei Elementarereignisse a1: „Pullover“, a2: „Hose“ und a3: „Schuhe“, also A=(a1;a2;a3). Der Mathematiker führt jetzt den Begriff des „Tupels“ ein. Unser Ereignis A ist ein 3–Tupel, 3-Tupel deshalb, weil es sich aus drei Elementarereignissen zusammensetzt. Tupel ist ein Erweiterungsbegriff zum Begriff Paar. Ein Paar besteht ja aus zwei Elementen, ist im mathematischen Begriff somit ein 2–Tupel. Da die Anzahl der Elemente aber variabel sein kann, führen wir den Begriff des k–Tupels ein. Das k steht also für die Anzahl der Elemente eines Ereignisses. Ein Ereignis E als k–Tupel hat die Elemente (e1;e2;e3;…ek). Jetzt stellen wir die Mächtigkeit der Elementarereignisse fest. a1 hat genau n1=5 Auswahlmöglichkeitgen, a2 hat genau n2=3 Auswahlmöglichkeiten und für a3 ist n3=2. |
| Das allgemeine Zählprinzip für Mengen (für k–Tupel) besagt nun folgendes: | ||||||||||||||||||||||||||||
Merksatz allgemeines Zählprinzip
|
||||||||||||||||||||||||||||
| Bezogen auf unser Beispiel heißt dies, dass Horst genau über 5⋅3⋅2=30 verschiedene Outfits verfügt. | ||||||||||||||||||||||||||||
3. Teilbereiche der stochastischen Kombinatorik
| Zunächst müssen wir unterscheiden, ob alle Elemente eines Tupels zu berücksichtigen sind oder nur einzelne Elemente. In unserem obigen Beispiel sind alle Elemente des 4-er, 3-er sowie 2-er-Tupels zu berücksichtigen. Beim klassischen Lottospiel 6 aus 49 beispielsweise sind aus dem 49-er Tupel nur 6 Elemente zu berücksichtigen. Bei einem 4-gliedrigen Zahlenschloss (Fahrrad) haben wir ja in jeder Zahlenreihe ein 10-er Tupel, von jedem 10er-Tupel ist aber nur ein einziges Element zu berücksichtigen. Im ersten Fall sprechen wir von einer Permutation, im zweitem Fall von einer Kombination und im 3. Fall von einer Variation. |
3.1. Die Permutation
| Aus dem allgemeinen Zählprinzip lassen sich Formeln für einige wichtige spezielle Auswahlprozesse ableiten. |
Merksatz Permutation
| Gegeben sei eine Menge A der Mächtigkeit |A|=k. Eine Anordnung aller k Elemente in einer bestimmten Reihenfolge heißt Permutation der Elemente von A. | |||
| Eine Permutation einer k–elementigen Menge ist also ein k–Tupel, in dem jedes Element der Menge (genau einmal) vorkommt. Um die Zahl der Permutationen zu berechnen, benötigen wir den Begriff der Fakultät. |
Merksatz Fakultät
| Die Fakultät einer natürlichen Zahl k ist das Produkt aller natürlichen Zahlen von 1 bis k, falls k≠0 und k≠1. Wir schreiben k⋅(k-1)⋅(k-2)⋅(k-3)∙…⋅3⋅2⋅1=k! und sprechen „k Fakultät“. Es wird weiterhin festgelegt, dass 0!=1 und 1!=1 ist. | |||
3.1.1. Beispiel 2
 Vor einem Wettlauf werden acht Bahnen unter den acht Läufern ausgelost, indem jeder ein Los aus einer Urne zieht (ohne Zurücklegen). Bestimmen Sie die Anzahl der möglichen Startaufstellungen. Vor einem Wettlauf werden acht Bahnen unter den acht Läufern ausgelost, indem jeder ein Los aus einer Urne zieht (ohne Zurücklegen). Bestimmen Sie die Anzahl der möglichen Startaufstellungen. |
| Der erste Läufer zieht eins von acht Losen, der zweite hat nur noch sieben zur Auswahl, der dritte nur noch sechs und so weiter. Mit den acht Läufern haben wir ein 8–Tupel. Der erste Läufer hat acht Auswahlmöglichkeiten, also ist n1=8. Der zweite Läufer hat nur noch 7 Auswahlmöglichkeiten, somit n2=7 usw., der achte Läufer hat n8=1. Wenden wir nun das allgemeine Zählprinzip an, kommen wir auf: |
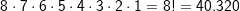 |
| mögliche Startaufstellungen. |
| Wesentlich in unseren Beispielen bislang ist die Tatsache, dass die Elemente a1;a2;a3;…;ak innerhalb des k–Tupels nicht mehrfach vorkommen. Im Beispiel 1 hatten wir es mit Pullover, Hosen und Schuhen zu tun; Im Beispiel 2 mit acht Läufern. Aus dieser Erkenntnis heraus leiten wir dann folgende Regel ab: |
Merksatz Permutation ohne Wiederholung
| Wenn ein Ereignis A aus den k–Tupeln (a1;a2;a3;…;ak) besteht, wobei sich die einzelnen k-Tupel nur durch die Anordnung der zur Verfügung stehenden k Elemente unterscheiden und keine Wiederholungen von Elementen auftreten, so beträgt die Gesamtzahl der Anordnungsmöglichkeiten oder Permutationen ohne Wiederholung: | ||
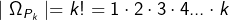 |
| Wenn wir nun festgestellt haben, dass dies nur gilt, wenn keine Wiederholungen auftreten, muss es ja wohl auch Fälle geben, in denen Wiederholungen auftreten. Ein typisches Beispiel für Permutationen mit Wiederholung sind Anagramme. Ein Anagramm ist die beliebige Umstellung eines Wortes, wobei die Wortlänge gleich bleibt. So ist z.B. TAPSA ein Anagramm des Wortes PASTA, ebenso wie TASAP oder PATSA. |
„PASTA“ ist ein 5–Tupel. Nach unsrer bisherigen Definition wäre die Gesamtzahl der Permutationen 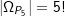 . Jetzt tritt der Buchstabe „A“ aber doppelt auf. Wir haben ja PA1STA2. Eines der Anagramme zu PASTA wäre besipielsweise „TAPSA“. Wir erkenne jetzt aber leicht, dass, wenn wir aus TA1PSA2 TA2PSA1 bilden, kein neues Anagramm entsteht. Daher reduziert sich die Anzahl der Permutationen auf . Jetzt tritt der Buchstabe „A“ aber doppelt auf. Wir haben ja PA1STA2. Eines der Anagramme zu PASTA wäre besipielsweise „TAPSA“. Wir erkenne jetzt aber leicht, dass, wenn wir aus TA1PSA2 TA2PSA1 bilden, kein neues Anagramm entsteht. Daher reduziert sich die Anzahl der Permutationen auf 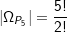 . . |
Die Anzahl der Permutationen des Wortes „PASTA“ beträgt 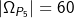 . . |
| Aus den Beispielen 3 und 4 heraus müssen wir die Regel zur Feststellung der Anzahl von Permutationen erweitern auf: |
Merksatz Permutation mit Wiederholung
| Wenn ein Ereignis A aus den k–Tupeln (a1;a2;a3;…;ak) besteht, wobei sich die einzelnen k-Tupel nur durch die Anordnung der zur Verfügung stehenden k Elemente unterscheiden und Wiederholungen auftreten, sind also Elemente mehrfach vorhanden und zwar das Element ak nk-mal, so beträgt die Gesamtzahl der Permutationen mit Wiederholung: | ||
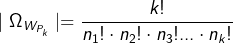 mit (n1+n2+n3+...+nk)=k mit (n1+n2+n3+...+nk)=k |
| Titel Aufgabenblatt | Level / Blattnr. |
Kombinatorik Aufgabenblatt Level 1 / Blatt 1  xx Aufgaben im Blatt |
| Du befindest dich hier: |
| Kombinatorik in der Stochastik |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 25. Juni 2022 25. Juni 2022

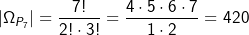 .
.

