|
Stochastik Urnenmodelle Fortgeschritten - Aufgabenblatt 1 |
| Dokument mit 8 Aufgabe |
Aufgabe A1 (2 Teilaufgaben)
| In einer Schachtel liegen fünf weiße Kugeln und eine schwarze Kugel. Aus der Schachtel wird wiederholt eine Kugel zufällig gezogen. Ist die gezogene Kugel schwarz, wird sie in die Schachtel zurückgelegt. Ist sie weiß, wird an ihrer Stelle eine schwarze Kugel in die Schachtel gelegt. | ||
| a) | Aus der Schachtel wird dreimal gezogen. Berechnen Sie die Wahrscheinlichkeiten der Ereignisse: | |
| A: | "Genau eine Kugel ist schwarz." | |
| B: | "Mindestens eine Kugel ist schwarz." | |
| b) | Wie oft muss man mindestens ziehen, um mit einer Wahrscheinlichkeit von mehr als 99,9 % mindestens eine weiße Kugel zu erhalten? | |
| |
Aufgabe A2 (2 Teilaufgaben)
| In einer Urne befinden sich zwei rote und eine bestimmte Anzahl schwarzer Kugeln. Es werden zwei Kugeln mit einem Griff gezogen. | ||
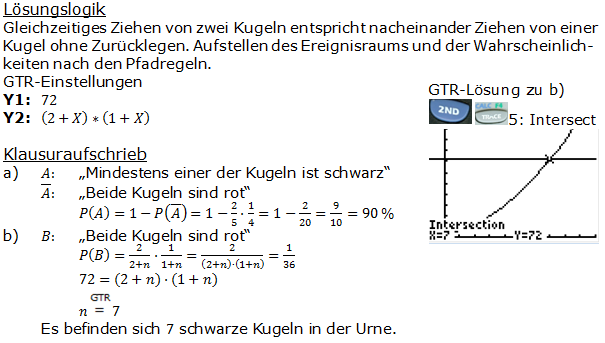
| a) | Mit welcher Wahrscheinlichkeit ist mindestens eine der Kugeln schwarz, wenn die Urne drei schwarze Kugeln enthält? | |
| b) | Die Wahrscheinlichkeit, dass beide Kugeln rot sind, beträgt nun 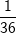 . Wie viele schwarze Kugeln sind in der Urne? . Wie viele schwarze Kugeln sind in der Urne? |
|
| |
Aufgabe A3 (2 Teilaufgaben)
| In einer Urne befinden sich fünf rote und eine bestimmte Anzahl schwarzer Kugeln. Insgesamt passen höchstens 50 Kugeln in die Urne. Aus der Urne werden nacheinander zwei Kugeln ohne Zurücklegen gezogen. | ||
| a) | Wie groß ist die Wahrscheinlichkeit, dass die Kugeln verschiedene Farben haben, wenn in der Urne zwei schwarze Kugeln sind? | |
| b) | Wie groß muss die Anzahl der schwarzen Kugeln in der Urne sein, damit die Wahrscheinlichkeit, zwei verschiedene Farben zu ziehen, maximal ist? | |
| |
Aufgabe A4 (2 Teilaufgaben)
| Ein Betrieb produziert Schrauben, die mit einer Wahrscheinlichkeit von 25 % fehlerhaft sind. Vor der Auslieferung an den Kunden werden die Schrauben durch ein Prüfgerät kontrolliert. Das Prüfgerät findet 95 % der fehlerhaften Schrauben, hält aber auch 10 % der einwandfreien Schrauben für fehlerhaft. Diese Schrauben kommen nicht in der Verkauf. |
||
| a) | Bestimme die Wahrscheinlichkeit der folgenden Ereignisse: | |
| A: | „Eine fehlerhafte Schraube kommt in den Verkauf.“ | |
| B: | „Eine einwandfreie Schraube wird nicht verkauft.“ | |
| C: | „Das Prüfgerät trifft eine falsche Entscheidung. | |
| b) | Das Prüfgerät soll so verbessert werden, dass die Wahrscheinlichkeit für eine falsche Entscheidung höchstens 2 % beträgt. Dazu soll der Anteil p der einwandfreien Schrauben, die das Prüfgerät fehlerhaft aussortiert, gesenkt werden. Wie groß darf p höchstens sein? | |
| |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021