 |
Stochastik Urnenmodelle Grundlagen - Aufgabenblatt 1 |
| Dokument mit 21 Aufgabe |
Aufgabe A1 (3 Teilaufgaben)
Ein Glücksrad hat drei Sektoren mit den Farben Rot, Gelb und Grün. Das Rad bleibt mit einer Wahrscheinlichkeit von 0,1 so stehen, dass der Zeiger in den roten Sektor zeigt, und mit einer Wahrscheinlichkeit von 0,3 so, dass der Zeiger in den gelben Sektor zeigt.
|
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (3 Teilaufgaben)
| In einem Karton sind zwei Dosen mit je 20 Keksen. Dose I enthält 12 Kekse mit Schokolade, Dose II nur vier. Es wird zufällig eine Dose ausgewählt und ein Keks herausgenommen. | |
| a) | Bestimme die Wahrscheinlichkeit für das Ereignis : A: "Der gewählte Keks ist ein Schokoladenkeks". |
| b) | Beweise, dass P(A) gleich bleibt, wenn die vorhandenen Kekse anders auf die beiden Dosen verteilt werden, wobei aber jede Dose nach wie vor insgesamt 20 Kekse enthält. |
| Eine Frage stellen... |
Aufgabe A3 (2 Teilaufgaben)
| In einer Urne befinden sich drei weiße und fünf schwarze Kugeln. Es werden zwei Kugeln mit Zurücklegen gezogen. | |
| a) | Berechne, wie groß die Wahrscheinlichkeit ist, dass mindestens eine der gezogenen Kugeln weiß ist. |
| b) | Ermittle, wie viele weiße Kugeln zusätzlich in die Urne getan werden müssen, damit die in Aufgabenteil a) berechnete Wahscheinlichkeit auf den Wert  ansteigt. |
| Eine Frage stellen... |
Aufgabe A4
| In einer Lostrommel sind vier Nieten und zwei Gewinnlose. Ein Kunde kauft so lange Lose, bis er alle Gewinnlose besitzt. Berechne, wie groß die Wahrscheinlichkeit ist, dass er höchstens vier Käufe tätigen muss. |
| Eine Frage stellen... |
Aufgabe A5 (2 Teilaufgaben)
| In einem Behälter befinden sich zwi rote und vier scharze Kugeln. | |
| a) | Es werden nacheinander zwei Kugeln mit Zurüklegen gezogen. Mit welcher Wahrscheinlichkeit haben beide Kugeln die gleiche Farbe? |
| b) | Es werden nun nacheinander zwei Kugeln ohne Zurüklegen gezogen. Berechne die Wahrscheinlichkeit, dass mindestens eine der beiden Kugeln rot ist. |
| Eine Frage stellen... |
Aufgabe A6 (2 Teilaufgaben)
| Mit einem idealen Würfel wird zweimal gewürfelt. | |
| a) | Wie groß ist die Wahrscheinlichkeit, dass mindestens eine 6 fällt? |
| b) | Mit welcher Wahrscheinlichkeit ist die Augenzahl beim zweiten Wurf größer als beim ersten? |
| Eine Frage stellen... |
Aufgabe A7 (3 Teilaufgaben)
| In einer Urne liegen zwei rote und drei blaue Kugeln. Es werden nacheinander zwei Kugeln wie folgt gezogen: | |
| Ist die erste Kugel rot, wird sie in die Urne zurückgelegt. | |
| Ist die erste Kugel blau, so wird sie nicht zurückgelegt. | |
| Berechne die Wahrscheinichkeiten der Ereignisse: | |
| a) | A: "Die zweite Kugel ist rot". |
| b) | B: "Die zweite Kugel ist blau". |
| c) | C: "Die zwei Kugeln haben verschiedene Farben". |
| Eine Frage stellen... |
Aufgabe A8
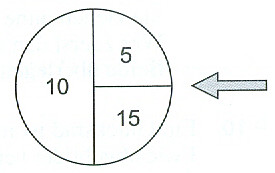 Das nebenstehende Glücksrad wird dreimal gedreht.Berechne die Wahrscheinlichkeit der Ereignisse:
|
|||||||
| Eine Frage stellen... |
Aufgabe A9 (2 Teilaufgaben)
| Ein Tennismatch besteht aus drei Sätzen. Das Match gewinnt der Spieler, der zuerst zwei Sätze für sich entscheidet. Erfahrungsgemäß gewinnt Felix gegen Max zwei von drei Sätzen. | |
| a) | Mit welcher Wahrscheinlichkeit dauert da Match nur zwei Sätze? |
| b) | Mit welcher Wahrscheinlichkeit kann Max das Match für sich entscheiden? |
| Eine Frage stellen... |
Aufgabe A10 (2 Teilaufgaben)
| In einer Schachtel liegen sechs gleich große Zettel, auf denen je ein Wort des Satzes "In der Kürze liegt die Würze" steht. | |
| a) | Aus der Schachtel wird zufällig ein Zettel gezogen. Die Zufallsvariable X gibt die Anzahl der Buchstaben des gezogenen Wortes an. Welche Werte kann X annehmen? |
| b) | Es werden nun so lange Zettel ohne Zurücklegen aus der Schachtel gezogen, bis man ein Wort mit fünf Buchstaben erhält. Die Zufallsvariable Y gibt die Anzahl der Ziehungen an. Welche Werte kann Y annehmen? Berechne P(Y≤2). |
| Eine Frage stellen... |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021
