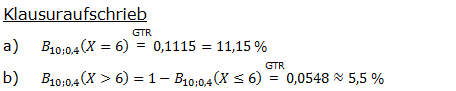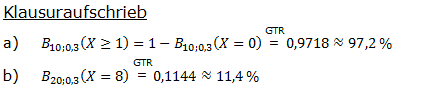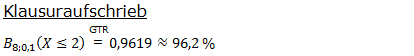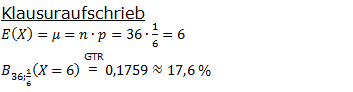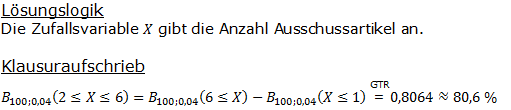 |
Stochastik Binomialverteilung Level 1 - Grundlagen - Aufgabenblatt 3 |
| Dokument mit 26 Aufgabe |
Aufgabe A1 (2 Teilaufgaben)
| Ein Jäger trifft sein Ziel mit einer Wahrscheinlichkeit 40 %. Mit welcher Wahrscheinlichkeit erzielt er bei zehn Schüssen | |
| a) | genau sechs Treffer |
| b) | mehr als sechs Treffer? |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (2 Teilaufgaben)
| Bei einem Automaten gewinnt man in 30 % aller Spiele. Wie groß ist die Wahrscheinlichkeit, dass man | |
| a) | bei 10 Spielen mindestens einmal gewinnt? |
| b) | bei 20 Spielen achtmal gewinnt? |
| Eine Frage stellen... |
Aufgabe A3
| In einem "Nachrichtenkanal" wird ein Zeichen mit der Wahrscheinlichkeit p=0,9 richtig übertragen. Eine Nachricht besteht aus acht Zeichen. Mit welcher Wahrscheinlichkeit werden höchstens zwei Zeichen falsch übertragen? |
| Eine Frage stellen... |
Aufgabe A4
| Ein fairer Würfel wird 36-mal geworfen. Berechne die Wahrscheinlichkeit dafür, dass die Augenzahl 6 in der erwarteten Anzahl eintritt. |
| Eine Frage stellen... |
Aufgabe A5
| Eine Firma produziert einen bestimmten Massenartikel mit einem Ausschussanteil von 4 %. Berechne die Wahrscheinlichkeit, dass sich unter 100 zufällig ausgewählten Artikeln mindestens 2 und höchstens 6 Ausschussartikel befinden. |
| Eine Frage stellen... |
Aufgabe A6 (3 Teilaufgaben)
| Die Musikgesellschaft "Harmonie" führt ihr Jubiläumskonzert durch. In den Pausen werden Tombola-Lose angeboten. Die Wahrscheinlichkeit für einen Gewinn ist 10 %. | |
| a) | Fritz ist ein eifriger Loskäufer. 490 Lose hat er schon gekauft und 10 Gewinne erzielt. Wie groß ist die Wahrscheinlichkeit, dass man bei 90 Losen höchstens 10-mal gewinnt? |
| b) | Hans hat schon 100 Lose gekauft und dabei 16 Gewinne eingestrichen. Er behauptet, er habe eben eine besonders begabte Hand. Mit welcher Wahrscheinlichkeit kommt man ohne besondere Begabung auf mindestens 16 Treffer? |
| c) | Die Besucher können auch Säckchen kaufen, die je 10 zufällig ausgewählte Lose enthalten. Der Veranstalter verspricht mindestens einen Gewinn, ansonsten wird das Geld zurückerstattet. Wie groß ist das Risiko, dass der Veranstalter zahlen muss? |
| Eine Frage stellen... |
Aufgabe A7 (2 Teilaufgaben)
| Wie oft muss man einen idealen Würfel mindestens werfen, wenn man mit einer Wahrscheinlichkeit von | |||
| a) | mehr als 90 % | b) | mehr als 99 % |
| mindestens eine Sechs haben will? | |||
| Eine Frage stellen... |
Aufgabe A8 (7 Teilaufgaben)
| Die Zufallsvariable X ist binomialverteilt mit den Parametern n=30 und p=0,25. Berechne: | |||||
| a) | P(X=10) | b) | P(X≤10) | c) | P(X>5) |
| d) | P(15<X<25) | e) | den Erwartungswert von X | ||
| f) | Für welchen Wert k wird P(X=k) maximal? | ||||
| g) | Erstelle mit dem GTR/WTR mit Hilfe von 2 Listen eine Wertetabelle für die Zuordnung k⟶P(X=k). | ||||
| Eine Frage stellen... |
Aufgabe A9 (3 Teilaufgaben)
| Ein Spielwürfel mit den Augenzahlen 1 bis 6 wird 18-mal geworfen. Berechne die Wahrscheinlichkeiten der folgenden Ereignisse. Gib die Ereignisse in Prozent an und runde auf eine Dezimale. |
|
| A: | Es wird 6-mal eine Augenzahl gewürfelt, die größer als 4 ist. |
| B: | Es wird mehr als 4-mal eine Augenzahl gewürfelt, die größer als 4 ist. |
| C: | Es wird mindestens 4-mal aber höchstens 7-mal eine Augenzahl gewürfelt, die größer als 4 ist. |
| Eine Frage stellen... |
Aufgabe A10 (2 Teilaufgaben)
| In einer Fabrik werden die hergestellten Teile von einer Kontrolleurin überprüft, die jedes Teil mit einer Wahrscheinlichkeit von 97 % richtig beurteilt. | |
| a) | Ab welcher Anzahl von untersuchten Teilen ist die Wahrscheinlichkeit, dass die Kontrolleurin mindestens eines davon falsch beurteilt, größer als 99,9 %? |
| b) | Bei einer anderen Kontrolleurin liegt die Wahrscheinlichkeit, von 100 untersuchten Teilen mindestens drei falsch zu beurteilen, bei etwa 75 %. Mit welcher Wahrscheinlichkeit beurteilt diese Kontrolleurin ein von ihr untersuchtes Teil falsch? (Ergebnis in Prozent, auf eine Dezimale gerundet). |
| Eine Frage stellen... |
Aufgabe A11 (2 Teilaufgaben)
| In einer Urne sind 400 schwarze und 600 weiße Kugeln. | ||
| a) | Aus dieser Urne werden nacheinander 5 Kugeln mit Zurücklegen gezogen. Bestimmen Sie die Wahrscheinlichkeiten der Ereignisse | |
| A: | Die fünf Kugeln haben dieselbe Farbe. | |
| B: | Es sind mehr schwarze als weiße Kugeln. | |
| C: | Die Kugel, die im vierten Zug gezogen wird, ist mindestens die dritte weiße Kugel. | |
| b) | Nun wird 100-mal eine Kugel mit Zurücklegen gezogen. Wie groß ist die Wahrscheinlichkeit, dass die Zahl der gezogenen schwarzen Kugeln um höchstens 5 vom Erwartungswert abweicht? |
|
| Eine Frage stellen... |
Aufgabe A12 (2 Teilaufgaben)
| Bei dem abgebildeten Glücksrad sind die Mittelpunktswinkel der Kreisausschnitte gleich groß. Das Glücksrad wird mehrfach gedreht und nach jeder Drehung wird die Zahl beim Pfeil notiert. |  |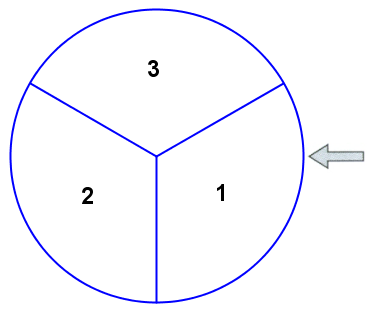
||
| a) | Mit welcher Wahrscheinlichkeit erhält man bei vier Drehungen | ||
| - | nur bei der letzten Drehung die Zahl 1, | ||
| - | mindestens einmal die Zahl 1, | ||
| - | genau zweimal die Zahl 1 und zwar bei direkt aufeinanderfolgenden Drehungen? | ||
| b) | Das Glücksrad wird n-mal gedreht. Für ein Ereignis A gilt: |
||
 |
|||
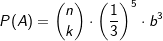| Gib geeignete Werte für n, k und b an und beschreibe ein mögliches Ereignis A in Worten. | |||
| Eine Frage stellen... |
| Du befindest dich hier: |
| Stochastik Binomialverteilung Level 1 - Grundlagen - Aufgabenblatt 3 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021
