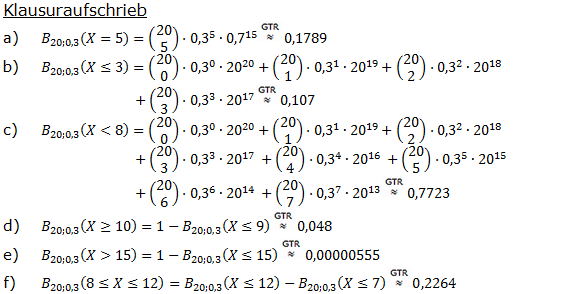 |
Stochastik Binomialverteilung Fortgeschritten - Aufgabenblatt 2 |
| Dokument mit 20 Aufgabe |
Aufgabe A1 (6 Teilaufgaben)
| Stelle zunächst die Bernoulliformel auf und berechne dann mit dem GTR/WTR, mit welcher Wahrscheinlichkeit man bei einer Bernoulli-Kette der Länge n=20 und der Wahrscheinlichkeit p=0,3 | |||
| a) | fünf Treffer, | b) | höchstens drei Treffer, |
| c) | weniger als acht Treffer, | d) | mindestens zehn Treffer, |
| e) | mehr als 15 Treffer, | f) | mindestens 8 und höchstens 12 Treffer |
| erhält. | |||
 Eine Frage stellen... |
Fehler melden...Aufgabe A2
| Ein Hersteller von Schrauben behauptet, dass mindestens 98 % der Schrauben normgerechte Längen haben. Ein Händler kontrolliert eine Schraubenlieferung mit einer Stichprobe vom Umfang 200 und findet k Schrauben mit nicht normgerechter Länge. |
| Die Lieferung soll zurückgewiesen werden, wenn die Wahrscheinlichkeit für mindestens k nicht normgerechte Schrauben in der Stichprobe höchstens 5 % beträgt. Ab welcher Anzahl k sollte er die Lieferung zurückweisen? |
| Eine Frage stellen... |
Aufgabe A3
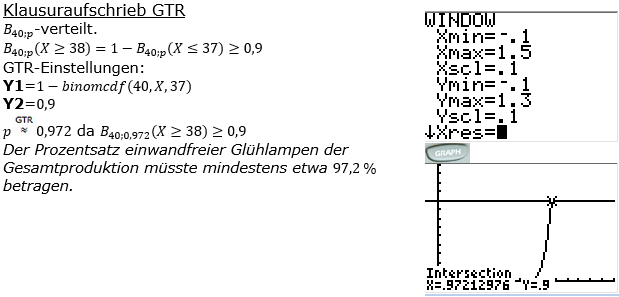
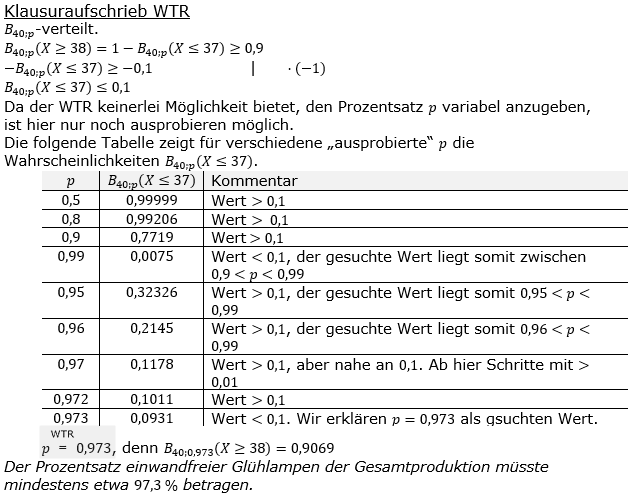
| Eine Glühlampe, die zufällig der Produktion entnommen wird, leuchtet einwandfrei mit der unbekannten Wahrscheinlichkeit p. |
| Jemand entnimmt zufällig 40 Glühlampen. Mit einer Wahrscheinlichkeit von mindestens 90 % sollen mindestens 38 Glühlampen dieser Stichprobe einwandfrei sein. Wie groß muss die Wahrscheinlichkeit p mindestens sein? |
| Eine Frage stellen... |
Aufgabe A4
| Ein Zahnarzt weiß, dass die Wahrscheinlichkeit dafür, bei einem Patienten Karies zu diagnostizieren, etwa p=0,8 beträgt. |
| Wie viele Karteikarten muss man der Patientenkartei zufällig entnehmen, wenn dabei mit einer Wahrscheinlichkeit von mindestens 95 % drei oder mehr Patienten mit Kariesbefund sein sollen? |
| Eine Frage stellen... |
Aufgabe A5 (2 Teilaufgaben)
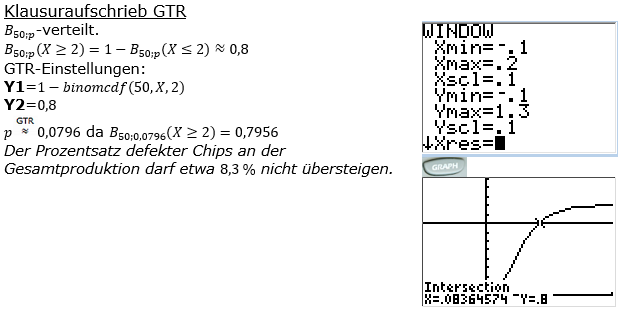
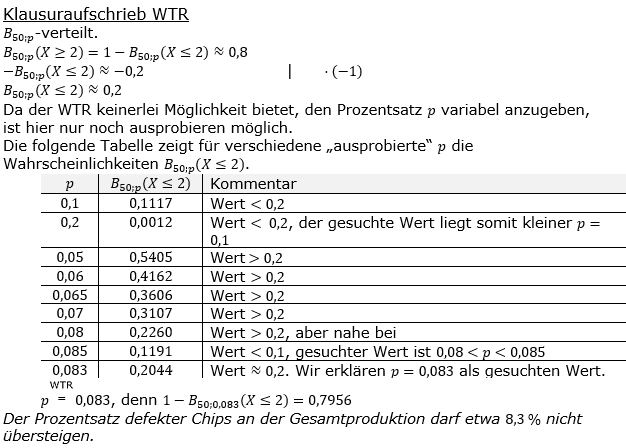
| Statistische Untersuchungen ergaben, dass bei einer Produktion von Computerchips 1 % fehlerbehaftet sind. | |
| a) | Wie viele Chips muss man mindestens überprüfen, damit die Wahrscheinlichkeit, darunter mindestens einen defekten Chip zu finden, größer als 90 % ist? |
| b) | Aufgrund eines Gerätefehlers erhöht sich der Anteil der fehlerhaften Chips in der Produktion. Die Wahrscheinlichkeit, unter 50 untersuchten Chips mindestens zwei defekte zu finden, liegt jetzt bei etwa 80 %. Bestimme den Anteil der defekten Chips in dieser Produktion. (Ergebnis in Prozent, auf eine Dezimale gerundet) |
| Eine Frage stellen... |
Aufgabe A6 (2 Teilaufgaben)
| Ein Großhändler bezieht von zwei Herstellern A und B Energiesparlampen, die äußerlich nicht zu unterscheiden sind. Erfahrungsgemäß sind 9,6 % der Lampen von Hersteller A und 4,6 % der Lampen von Hersteller B defekt. | |
| a) | Mit welcher Wahrscheinlichkeit sind in einer Packung mit 10 Lampen von Hersteller A alle intakt? |
| b) | Bei einer Inventur stellt der Großhändler fest, dass 6 % aller Lampen defekt sind. Berechnen Sie die Anteile der Hersteller A und B an den gelieferten Lampen. |
| Eine Frage stellen... |
Aufgabe A7 (3 Teilaufgaben)
| Ein Medikament heilt eine bestimmte Krankheit mit einer Wahrscheinlichkeit von 85 %. Eine Gruppe von 100 erkrankten Patienten erhält das Medikament. Mit welcher Wahrscheinlichkeit werden | ||
| - | höchstens 80, | |
| - | mindestens 40 und höchstens 90, | |
| - | mindestens 85 | |
| Patienten dieser Gruppe geheilt? Wie groß darf eine Gruppe höchstens sein, damit mit mindestens 50 % Wahrscheinlichkeit alle Patienten der Gruppe geheilt werden? |
||
| Eine Frage stellen... |
Aufgabe A8 (2 Teilaufgaben)
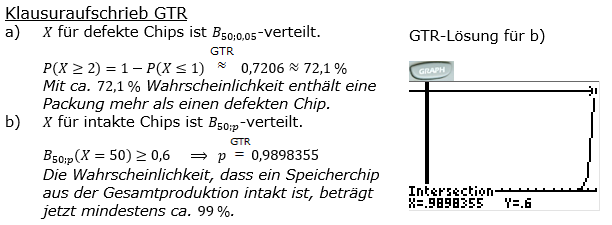
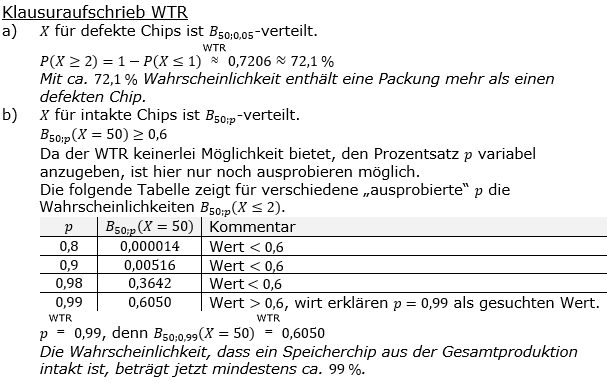
| Eine Firma stellt Speicherchips her, die mit der Wahrscheinlichkeit p intakt sind. Man geht nach Erfahrungswerten von p=0,95 aus. | |
| a) | Mit welcher Wahrscheinlichkeit enthält eine Packung mit 50 Chips mehr als einen defekten Speicherchip? |
| b) | Nach einer Optimierung der Produktion versichert die Firma, dass mit einer Wahrscheinlichkeit von mindestens 60 % in einer Packung mit 50 Chips alle intakt sind. Wie groß ist p dann mindestens? |
| Eine Frage stellen... |
Aufgabe A9 (2 Teilaufgaben)
 Ein Glücksrad hat die Felder G und N. Das Feld G erscheint mit der Wahrscheinlichkeit 0,6 und das Feld N mit der Wahrscheinlichkeit 0,4. Bei einem Spiel wird das Glücksrad fünfmal gedreht. Man gewinnt, wenn dabei mindestens viermal G erscheint. |
|
| a) | Berechnen Sie die Wahrscheinlichkeit p, dass man bei diesem Spiel gewinnt. |
| b) | Max spielt dieses Spiel 20-mal. Mit welcher Wahrscheinlichkeit gewinnt er dabei mindestens 6 Spiele? Wie groß ist die Wahrscheinlichkeit, dass er beim 20. Spiel zum sechsten Mal gewinnt? |
| Eine Frage stellen... |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 03. November 2024 03. November 2024
