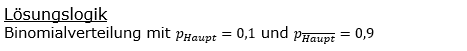 |
Stochastik Binomialverteilung Fortgeschritten - Aufgabenblatt 3 |
| Dokument mit 15 Aufgabe |
Aufgabe A1 (2 Teilaufgaben)
| Zwei Maschinen M1 und M2 stellen die gleiche Sorte Schrauben her. Erfahrungsgemäß sind 1 % der von Maschine M1 produzierten Schrauben fehlerhaft. Bei Maschine M2 sind es 5 %. | ||
| a) | Berechne die Wahrscheinlichkeiten der Ereignisse: | |
| A: | "Von 100 Schrauben aus der Maschine M1 sind höchstens zwei fehlerhaft". | |
| B: | "Von 200 Schrauben aus der Maschine M2 sind mehr als 180, aber höchstens 190 einwandfrei". | |
| b) | Die Schrauben werden in Beutel zu jeweils 500 Stück verpackt und mit einem Aufkleber versehen, auf dem die Maschine vermerkt ist, die sie produziert hat. Gelegentlich fallen diese Aufkleber beim Transport der Beutel ab. In diesem Fall werden einem solchen Beutel 50 Schrauben entnommen und überprüft. Bei höchstens einer fehlerhaften Schraube wird der Beutel der Maschine M1, ansonsten der Maschine M2 zugeordnet. Mit welcher Wahrscheinlichkeit wird dabei ein Beutel mit Schrauben, die von der Maschine M1 produziert wurden, falsch zugeordnet? | |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (2 Teilaufgaben)
| Bei einem Glücksrad beträgt die Wahrscheinlichkeit für einen Hauptgewinn bei einer Drehung 10 %. | ||
| a) | Bestimme die Wahrscheinlichkeit, dass man bei 10 Drehungen des Rades | |
| - | genau einen Hauptgewinn, | |
| - | mindestens zwei Hauptgewinne | |
| erhält. | ||
| b) | Wie oft muss das Glücksrad mindestens gedreht werden, damit man mit mindestens 80 % Wahrscheinlichkeit zwei oder mehr Hauptgewinne erhält? | |
| Eine Frage stellen... |
Aufgabe A3 (4 Teilaufgaben)
| Ein Betrieb stellt Infrarotsensoren her, wobei erfahrungsgemäß 10 % der Sensoren defekt sind. Die Sensoren werden in Packungen zu 50 Stück ausgeliefert. | |
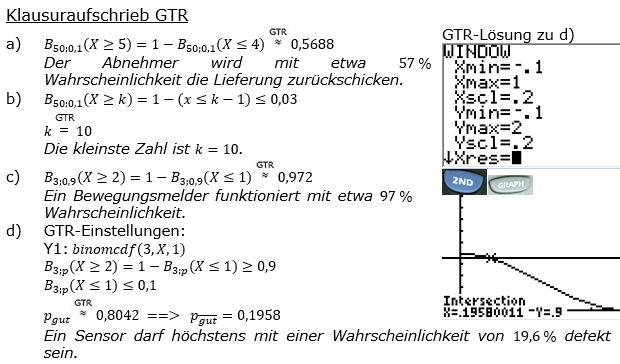
| a) | Ein Abnehmer überprüft eine Packung. Wenn er mehr als fünf defekte Sensoren darin findet, will er die Lieferung zurückschicken. Mit welcher Wahrscheinlichkeit ist dies der Fall? |
| b) | Der Betrieb verspricht, alle Packungen zurückzunehmen, die mehr als k defekte Sensoren enthalten. Bestimme die kleinste Zahl k, für die die Wahrscheinlichkeit einer Rücksendung bei 3 % liegt. |
| Eine Firma verwendet die Infrarotsensoren ungeprüft zur Herstellung von Bewegungsmeldern. In einen Bewegungsmelder werden drei Sensoren verbaut. Damit er funktioniert, müssen mindestens zwei Sensoren intakt sein. | |
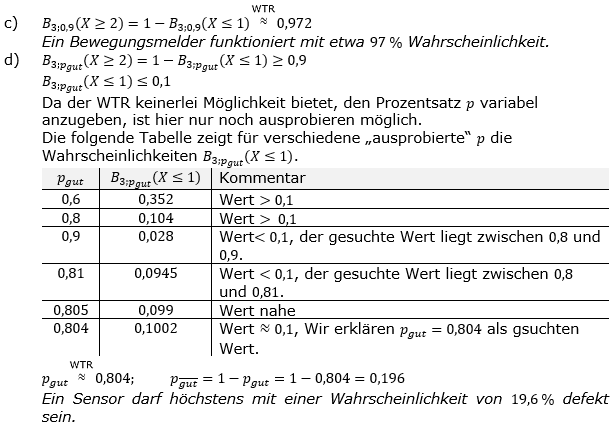
| c) | Mit welcher Wahrscheinlichkeit funktioniert ein Bewegungsmelder? |
| d) | Mit welcher Wahrscheinlichkeit p darf ein Sensor höchstens defekt sein, damit ein Bewegungsmelder mit einer Wahrscheinlichkeit von mindestens 90 % funktioniert? Bestimme p auf die zweite Nachkommastelle gerundet. |
| Eine Frage stellen... |
Aufgabe A4 (2 Teilaufgaben)
| Bei einer Fluggesellschaft ist aus langjähriger Erfahrung bekannt, dass ein Kunde mit einer Wahrscheinlichkeit von 5 % seinen gebuchten Flug nicht antritt. | |
| a) | Die Fluggesellschaft setzt für eine bestimmte Strecke eine kleine Maschine mit 70 Sitzplätzen ein. Wie groß ist die Wahrscheinlichkeit, dass bei 70 Buchungen tatsächlich alle Sitzplätze belegt sind? Die Fluggesellschaft überbucht die Maschine und verkauft 72 Flugtickets. Mit welcher Wahrscheinlichkeit kann dies dazu führen, dass nicht alle Passagiere mitfliegen können? |
| b) | Eine größere Maschine der Fluggesellschaft hat 300 Sitzplätze. Wie viele Tickets darf die Gesellschaft maximal verkaufen, wenn die Wahrscheinlichkeit, dass mehr als 300 Personen den Flug antreten wollen, weniger als 3 % betragen soll? |
| Eine Frage stellen... |
Aufgabe A5 (3 Teilaufgaben)
| Ein Ferienhotel hat 260 Zimmer, die in der Hauptsaison jeweils für eine Woche gebucht werden können. Der Hotelbesitzer weiß aus Erfahrung, dass im Mittel nur 90 % der Buchungen in Anspruch genommen werden. Der Rest wird kurzfristig storniert. Die Anzahl der Buchungen, die tatsächlich in Anspruch genommen werden, wird durch die Zufallsvariable X beschrieben. | |
| a) | Beschreibe, unter welcher Annahme man die Wahrscheinlichkeitsverteilung von mit einer Binomialverteilung modellieren kann. Beschreibe eine reale Situation, die gegen die Annahme spricht. |
| b) | Der Hotelbesitzer nimmt genauso viele Buchungen pro Woche an, wie Zimmer vorhanden sind. Mit welcher durchschnittlichen Anzahl an belegten Zimmern kann der Hotelbesitzer in einer Woche rechnen? Mit welcher Wahrscheinlichkeit wird mindestens diese Anzahl von Zimmern belegt? |
| c) | Um das Hotel möglichst gut auszulasten, erwägt der Hotelbesitzer 290 Buchungen pro Woche anzunehmen. Wie groß ist die Wahrscheinlichkeit, dass dann das Hotel zwei Wochen in Folge überbucht ist? Die Wahrscheinlichkeit für diesen Fall soll weniger als 0,5 % betragen. Wie viele Buchungen pro Woche darf der Hotelbesitzer dann höchstens annehmen? |
| Eine Frage stellen... |
Aufgabe A6 (2 Teilaufgaben)
| Für Kühlaggregate werden Pumpen verwendet, die das Kühlmittel transportieren. Eine Pumpe fällt in einem bestimmten Zeitraum mit der Wahrscheinlichkeit p aus. Das Kühlaggregat A besitzt nur eine Pumpe, das Aggregat B vier Pumpen. Die Pumpen in B arbeiten unabhängig voneinander und es darf höchstens eine Pumpe ausfallen, damit das Kühlaggregat B noch funktioniert. | |
| a) | Mit welcher Wahrscheinlichkeit fallt das Kühlaggregat B aus, wenn p=0,1 gilt? |
| b) | Stellen Sie die Ausfallwahrscheinlichkeit von B als Funktion von p dar. Für welche Werte von p ist die Ausfallwahrscheinlichkeit von Aggregat B geringer als die von Aggregat A? |
| Eine Frage stellen... |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021
