|
Stochastik Urnenmodelle Grundlagen - Aufgabenblatt 2 |
| Dokument mit 21 Aufgabe |
Aufgabe A1 (2 Teilaufgaben)
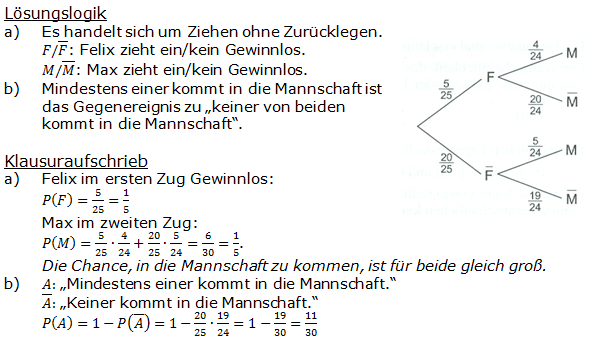
In einer Klasse von 25 Schülern soll für einen Wettbewerb eine Mannschaft von 5 Schülern gebildet werden. Da man sich nicht einigen kann, wird die Zusammensetzung der Mannschaft per Los bestimmt. In einer Lostrommel befinden sich 5 Gewinnlose und 20 Nieten. Der Reihe nach zieht jeder ein Los, ohne es zunächst zu öffnen. Felix zieht zuerst, Max als Zweiter.
|
| |
Aufgabe A2 (3 Teilaufgaben)
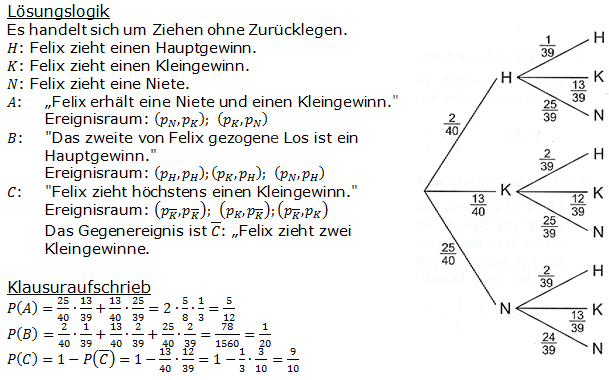
Bei einer Tombola verkauft eine Klasse 40 Lose. Unter diesen Losen sind 2 Hauptgewinne, 13 Kleingewinne und der Rest Nieten. Felix ist der erste Käufer und zieht nacheinander zwei Lose. Berechnen Sie die Wahrscheinlichkeiten der Ereignisse:
|
| |
Aufgabe A3 (2 Teilaufgaben)
In einer Klinik soll die Wirksamkeit eines neuen Medikaments getestet werden. Das Medikament wird in Packungen zu je 10 Tabletten an Patienten abgegeben. Man weiß, dass bei vielen Patienten auch Placebos (das sind Tabletten ohne Wirkstoff) die gleiche Wirkung haben wie die echten Tabletten. Daher wird in jeder Packung eine Tablette durch ein Placebo ersetzt.
|
| |
Aufgabe A4 (2 Teilaufgaben)
| In einer Schachtel liegen vier Tischtennisbälle, drei davon sind gelb und einer weiß. | |
| a) | Man zieht zweimal nacheinander mit Zurücklegen einen Ball aus der Schachtel. Mit welcher Wahrscheinlichkeit haben die Bälle verschiedene Farben? |
| b) | Max und Felix einigen sich auf folgendes Spiel: Sie ziehen ohne Zurücklegen abwechselnd jeweils einen Ball aus der Schachtel. Wer zuerst den weißen Ball zieht, hat gewonnen. Beide überlegen, ob es geschickt ist, den ersten Zug zu machen. |
| |
Aufgabe A5 (3 Teilaufgaben)
| Ein Glücksrad ist mit den Beschriftungen A, B und I wie abgebildet versehen. Die Mittelpunktswinkel der entsprechenden Kreisausschnitte haben die Weiten 90 °, 120 ° und 150 °. | ||
| Wie groß ist die Wahrscheinlichkeit, dass man bei drei Drehungen | 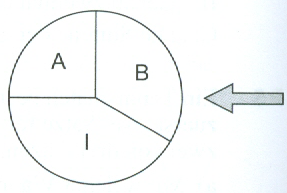 |
|
| a) | die Buchstaben in der Reihenfolge ABI, | |
| b) | mindestens einmal den Buchstaben B, | |
| c) | die Buchstabenfolge AB erhält? | |
| |
Aufgabe A6 (4 Teilaufgaben)
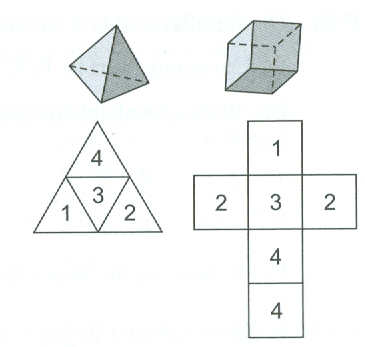
| Ein Tetraeder und ein Würfel werden gleichzeitig geworfen. Anders als beim Würfel gilt beim Tetraeder die Zahl als geworfen, die unten liegt. Die Seiten sind mit Zahlen wie in den Netzen abgebildet beschriftet. Berechne die Wahrscheinlichkeiten der Ereignisse: |
 |
|
| A: | "Man würfelt zwei ungerade Zahlen." | |
| B: | "Man erhält mindestens eine ungerade Zahl." | |
| C: | "Die Summe der Zahlen beträgt 6." | |
| D: | "Die Zahl auf dem Tetraeder ist kleiner als die auf dem Würfel." | |
| |
Aufgabe A7
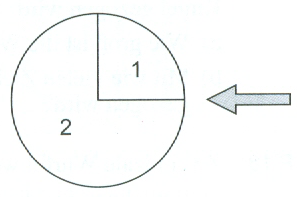 Das abgebildete Glücksrad wird zweimal gedreht. Mit welcher Wahrscheinlichkeit treten dabei nur gleiche Ziffern auf? Das abgebildete Glücksrad wird zweimal gedreht. Mit welcher Wahrscheinlichkeit treten dabei nur gleiche Ziffern auf?Beschreibe, wie man das einmalige Drehen des Glücksrades mithilfe einer idealen Münze simulieren könnte. |
| |
Aufgabe A8 (2 Teilaufgaben)
| Ein Glücksrad hat zwei Sektoren, beschriftet mit den Buchstaben G und N. Die Wahrscheinlichkeit für den Buchstaben G bei einer Drehung ist p. Das Glücksrad wird zweimal gedreht. | 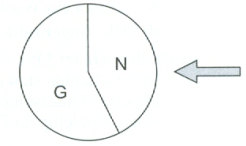 |
||
| a) | Bestimmen Sie für 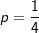 die Wahrscheinlichkeiten der Ereignisse: die Wahrscheinlichkeiten der Ereignisse: |
||
| A: | "Es erscheinen verschiedene Buchstaben." | ||
| B: | "Mindestens einmal erscheint der Buchstabe G." | ||
| b) | Die Wahrscheinlichkeit, dass mindestens einmal der Buchstabe N erscheint, ist 0,64. Wie groß ist dann p? | ||
| |
Aufgabe A9 (2 Teilaufgaben)
| Eine Urne enthält drei schwarze Kugeln, zwei rote Kugeln und eine grüne Kugel. | ||
| a) | Es werden nacheinander ohne Zurücklegen zwei Kugeln aus der Urne gezogen. Berechnen Sie die Wahrscheinlichkeiten der Ereignisse: | |
| A: | „Beide Kugeln haben verschiedene Farben." | |
| B: | "Die zweite Kugel ist schwarz oder grün." | |
| b) | Aus der Urne werden nacheinander vier Kugeln mit Zurücklegen gezogen. Wie groß ist die Wahrscheinlichkeit, dass genau eine rote Kugel dabei ist? | |
| |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 20. Juli 2021 20. Juli 2021