 |
Stochastik Erwartungswert Grundlagen - Aufgabenblatt 3 |
| Dokument mit 7 Aufgabe |
| Hinweis Bei Aufgaben zum Erwartungswert empfehlen wir dir, unmittelbar eine Tabelle der xi und P(X=xi) anzulegen. |
Aufgabe A1 (2 Teilaufgaben)
| Die SMV des ASG unterstützt jedes Jahr ein soziales Kinder- oder Jugendprojekt. Das Geld wird auf dem Schulfest mit einem Informationsstand und einem Glücksrad erwirtschaftet. Das Glücksrad wird zweimal gedreht. Folgende Gewinne sind vorgesehen: |  |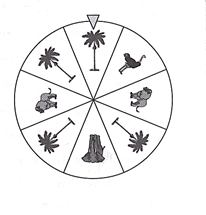
|
| Das Rad bleibt zweimal auf Elefant stehen: | 5,00 € | |
| Das Rad bleibt zweimal auf Elefant stehen: | 3,00 € | |
| Das Rad bleibt zweimal auf Elefant stehen: Die Einsätze hängen vom Alter der Kinder ab: |
1,50 € | |
| Schülerinnen/Schüler, Kinder und Jugendliche | 0,50 € | |
| Erwachsene | 1,00 € | |
| a) | Ermittle die Erwartungswerte der SMV getrennt für Schülerinnen/Schüler, Kinder und Jugendliche sowie für Erwachsene. | |
| b) | Die Endabrechnung am Ende des Schulfestes weist folgende Daten auf: Anzahl der Spiele von Schülerinnen/Schüler, |
|
| Kindern und Jugendlichen: | 372 | |
| Anzahl der Spiele Erwachsener: | 214 | |
| Gesamtgewinn: | 217,50 € | |
| Ermittle die Abweichung zwischen dem mit den Erwartungswerten ermittelten Gewinn und dem tatsächlichen Gewinn. Nenne mögliche Gründe für die festgestellte Abweichung. |
||
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (2 Teilaufgaben)
| Die Abschlussklassen des Linden-Gymnasiums in Tuttlingen organisieren zugunsten eines sozialen Projekts eine Tombola. Die Tabelle zeigt die Losverteilung und die damit jeweils verbundenen Gewinne. | |||
| Anzahl der Lose | Wert des Gewinns | ||
| 150 | Kein Gewinn | ||
| 40 Kleingewinne | Je 4,00 € | ||
| 10 Hauptgewinne | Je 20,00 € | ||
| Ein Los kostet 2,00 €. | |||
| a) | Berechne den Erwartungswert. | ||
| b) | Um den Gewinn für das soziale Projekt zu erhöhen, geben die Klassen 50 weitere Nieten in die Lostrommel. Welchen Betrag können die Abschlussklassen spenden, wenn alle Lose verkauft werden? |
||
| Eine Frage stellen... |
Aufgabe A3 (2 Teilaufgaben)
| Bei einer Wohltätigkeitsveranstaltung führt die Klasse 12 des ASG Heilbronn ein Glücksspiel durch. Die Sektoren des dafür verwendeten Glücksrades sind rot, gelb und blau gefärbt. Die Wahrscheinlichkeit für Rot beträgt 25 %, für Gelb  .Das Glücksrad wird einmal gedreht. Folgender Gewinnplan ist vorgesehen: |
|||
| Farbe | Gewinn | ||
| Rot | 4,00 € | ||
| Gelb | 1,50 € | ||
| Blau | 0,60 € | ||
| Pro Spiel werden 2,00 € Einsatz verlangt. | |||
| a) | Berechne den Erwartungswert. |
| b) | Die Klasse möchte ihren zu erwartenden Gewinn pro Spiel verdoppeln. Dabei soll das Glücksrad und der Einsatz pro Spiel nicht verändert werden. Stelle einen möglichen Gewinnplan auf. |
| Eine Frage stellen... |
Aufgabe A4
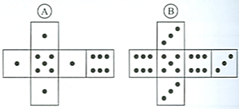
| Die beiden Netze zeigen die Augenzahlen zweier besonderer Spielwürfel. Beide Würfel werden gleichzeitig geworfen. Wie groß ist die Wahrscheinlichkeit, mindestens eine „Sechs“ zu werfen? |
 |
| Die beiden Würfel werden für ein | Wurfergebnisse | Gewinn | |
| Glücksspiel eingesetzt. Dazu wird nebenstehender Gewinnplan ge- | Gleiche Augenzahlen (Pasch) | 9,00 € | |
| prüft. Berechne den Erwartungswert. | Verschiedne Augenzahlen | Kein Gewinn | |
| Der Veranstalter möchte beim | Einsatz pro Spiel: 1,00 € | ||
Würfelnetz  die „Fünf“ durch |
|||
| eine „Sechs“ ersetzen. Der Gewinnplan soll gleich bleiben. Wäre dies für ihn vorteilhaft? Begründe. |
|||
| Eine Frage stellen... |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 20. Juli 2021 20. Juli 2021
