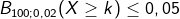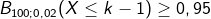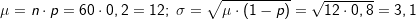Die Sigma-Regeln bieten einen Anhaltspunkt zur Feststellung einer Randgröße in den Fällen, in denen ein „Ausprobieren“ mangels fehlender Funktionalitäten eines Taschenrechners notwendig ist. Hierzu betrachten wir uns nachfolgendes
Beispiel 1
Ein Hersteller von Schrauben behauptet, dass mindestens 98 % der Schrauben normgerechte Längen haben. Ein Händler kontrolliert eine Schraubenlieferung mit einer Stichprobe vom Umfang 200 und findet k Schrauben mit nicht normgerechter Länge.
Die Lieferung soll zurückgewiesen werden, wenn die Wahrscheinlichkeit für mindestens k nicht normgerechte Schrauben in der Stichprobe höchstens 5 % beträgt.
Ab welcher Anzahl k sollte er die Lieferung zurückweisen? |
Lösung 1
Zunächst müssen wir festhalten, dass bei 98 % normgerechter Schrauben eben 2 % nicht normgerechte Schrauben vorhanden sind. Der Stichprobenumfang beträgt n=200, die Wahrscheinlichkeit für nicht normgerechte Schrauben somit p=0,02.
Die Aussage, dass sich höchstens 5 % nicht normgerechte Schrauben in der Stichprobe befinden, bedeutet, dass die kumulierte Wahrscheinlichkeit für X ≥ k nicht normgerechte Schrauben höchstens 0,05 sein darf. Mathematisch ausgedrückt: |
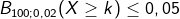 |
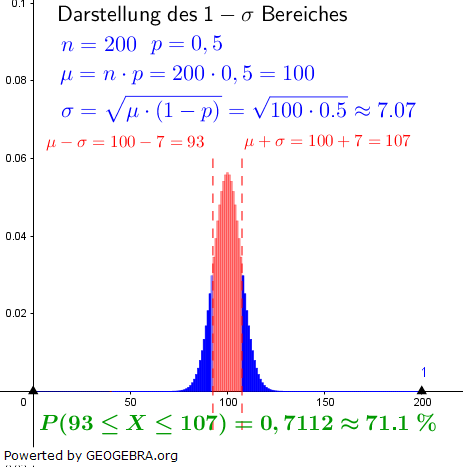
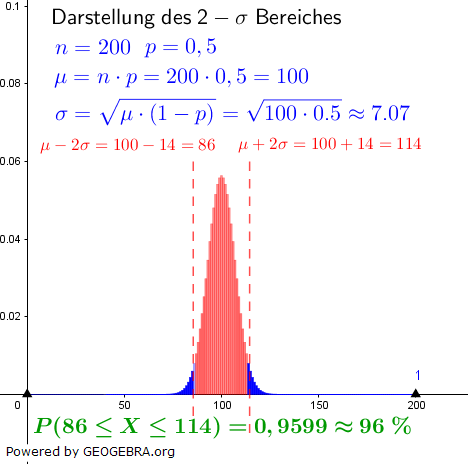
| Das Histogramm dieser Verteilung ist nachfolgend dargestellt. |
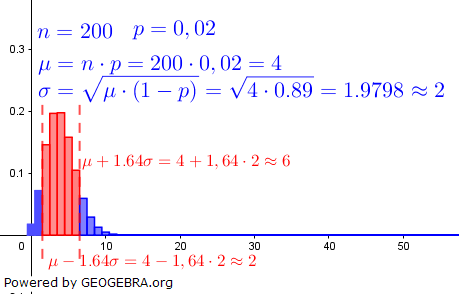 |
| Wir müssen die Formel B_(100;0,02) (X≥k)≤0,05 noch umstellen nach |
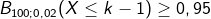 |
Eine kumulierte Wahrscheinlichkeit 0,95 befindet sich am rechten Rand des Histogramms. Da die σ-Regeln symmetrisch zum Erwartungswert liegen, sind die anderen 0,05 am linken Rand des Histogramms zu finden. Somit haben wir ein Sigma-Intervall von 100 %-2∙5,00 %=90 %. Gemäß oben angeführter Tabelle ist dies das 1,64σ-Intervall.
Da wir eine kumulierte Wahrscheinlichkeit ≥ 0,95 suchen, die ja am rechten Rand liegt, kommen wir in den Bereich des gesuchten k über k-1=μ+1,64σ, wodurch wir gerundet k-1=6 erhalten.
Wir beginnen die Berechnung der kumulierten Wahrscheinlichkeit mit k=6.
B100;0,02(X≤6)≈0,8914
Der errechnet Wert ist kleiner als 0,95. Wir erhöhen k um 1.
B100;0,02(X≤7)≈0,95066
Somit ist k-1=7 der gesuchte Wert. Aus k-1=7 folgt k=8.
Fazit:
Befinden sich mehr als 7 nicht normgerechte Schrauben in der Stichprobe, sollte der Händler die Lieferung zurückgeben. |
|



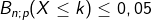
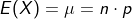
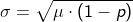
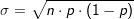 vor, gelten folgende Näherungen:
vor, gelten folgende Näherungen: