 |
WIKI Rentenrechnung mit Zinseszinsen |
wiki-rentenrechnung-mit-zinseszins_N.pdf
kapitel-rentenrechnung-mit-zinseszins_N.pdf
Einführung zur Rentenrechnung mit Zinseszinsen
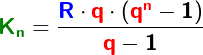
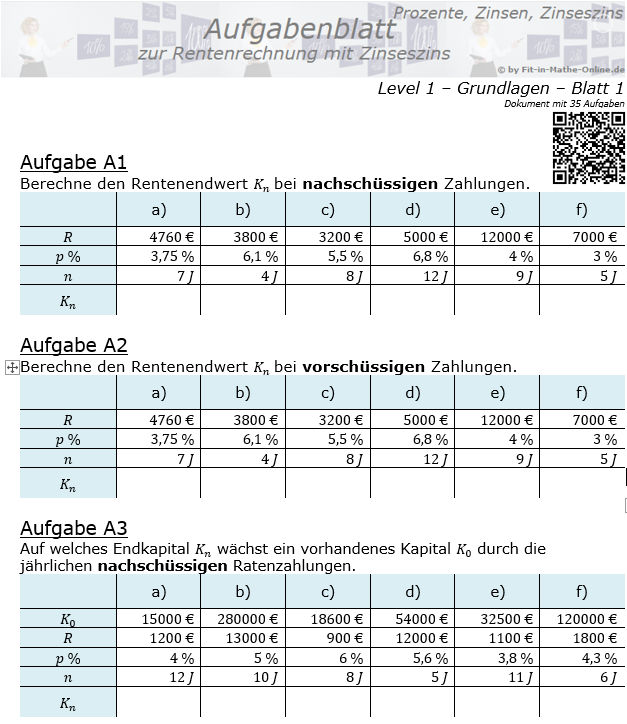
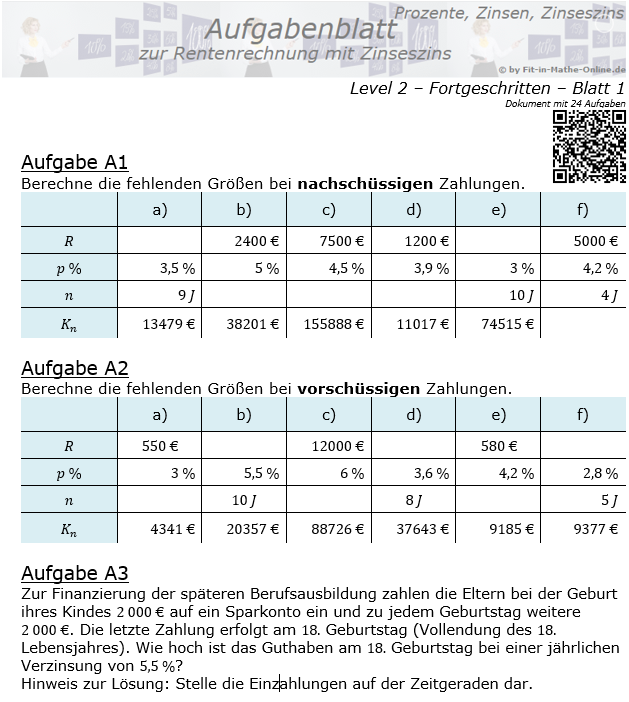
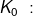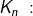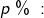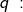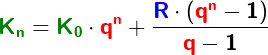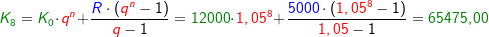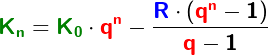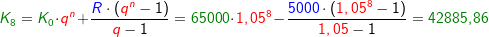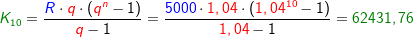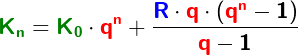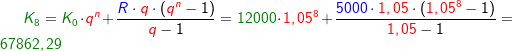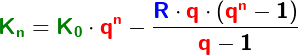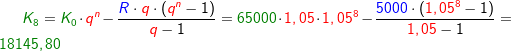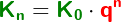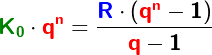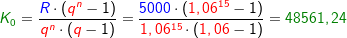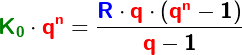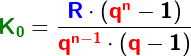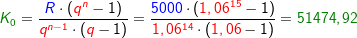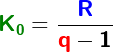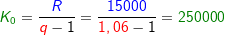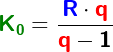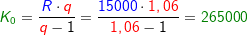| Im Kapitel Ratensparen haben wir Berechnungsformeln für die Berechnungen von Ratensparverträgen kennengelernt. In diesem Kapitel lernen wir nun eine andere und umfangreichere Berechnung dieser „Ratensparverträge“ kennen. Haben wir unter Ratensparen stets nur berechnet, nach wie vielen Raten eine bestimmtes Endkapital erreicht wird und haben dabei immer nur Einzahlungen am Anfang eines Jahres angenommen, ist es in der Rentenrechnung auch möglich, Einzahlungen am Ende eines Jahres vorzunehmen. Es entstehen dadurch zwei neue Begriffe, nämlich |
|
| • | Vorschüssige Rentenzahlungen sowie |
| • | Nachschüssige Rentenzahlungen |
| Weiterhin ist in der Rentenrechnung auch von Interesse, wie lange ein vorhandenes Kapital ausreicht, wenn man sich Jahr für Jahr einen bestimmten Betrag auszahlen lässt. Rentenrechnung ist also Ratensparen auf der einen Seite sowie Entnahmeplan auf der anderen Seite. Die wichtigsten Begriffe der Rentenrechnung – im folgenden Schritt für Schritt erläutert – sind somit: |
|
| • | Berechnung des Rentenendwertes, vorschüssig und nachschüssig |
| • | Berechnung des Rentenbarwertes, vorschüssig und nachschüssig |
| • | Regelmäßige Ein- bzw. Auszahlungen, vorschüssig und nachschüssig |
| • | Ewige Renten |
Der Rentenendwert
| Rentenendwerte sind die Werte, die nach Ablauf von regelmäßigen Einzahlungen (bzw. Auszahlungen) als effektiver Geldbetrag verfügbar sind. Wir merken uns: Ein- bzw. Auszahlungen zu Beginn eines Jahres werden „vorschüssige Zahlungen“ genannt. Ein- bzw. Auszahlungen am Ende eines Jahres werden „nachschüssige Zahlungen“ genannt. |
|
| Folgende Formelzeichen gelten bei der Verzinsung regelmäßiger Zahlungen: | |
 |
Anfangskapital |
 |
Endkapital |
 |
Zinssatz |
 |
Zinsfaktor mit  |
 |
Rate |
 |
Anzahl der jährlichen Zahlungen |
| Hinweis: Diese Formelzeichen haben wir bereits im Kapitel Ratensparen kennen gelernt. |
|
Der Rentenendwert mit nachschüssiger Zahlung
| Für den Endwert regelmäßiger nachschüssiger Zahlungen gilt: |
 |
Beispiele
Der Rentenendwert mit voschüssiger Zahlung
| Für den Endwert regelmäßiger vorschüssiger Zahlungen gilt: |
 |
Beispiele
Beispiel 4
| Herr Maier zahlt 10 Jahre lang am Anfang des Jahres 5 000 € auf ein Konto ein. Die Bank bietet einen Zinssatz von 4 %. Wie hoch ist das Endkapital nach dieser Zeit? |
| Gegeben: R=5000 €; p %=4 %, n=10 Gesucht: K10 |
 |
| Der Rentenendwert beträgt 62 431,76 €. |
| Hinweis:. Diese Berechnung hätte auch mit den Formeln aus dem Kapitel Ratensparen ausgeführt werden können. Wir erinnern uns an die Formel mit |
| Kn=R⋅(qn+qn-1+qn-2+...+q) |
| Die Berechnung mit dieser Formel bringt |
| K10=5000∙(1,0410+1,049+1,048+⋯+1,04)=5000∙12,48635=62431,76 |
| Es ergibt sich derselbe Rentenendwert |
Der Rentenbarwert
| Unter dem Rentenbarwert verstehen wir den einmalige Betrag K0, der bei einer Rentenanstalt einzuzahlen ist, um n Jahre lang entweder am Ende (nachschüssig) oder am Anfang (vorschüssig) eines jeden Jahres eine Rente von R € beziehen zu können bei einem festen Zinssatz von p %. |
Der Rentenbarwert mit nachschüssiger Zahlung
| Den nachschüssigen Barwert K0 erhalten wir durch Abzinsung des nachschüssigen Rentenendwertes Kn. Wir berechnen zunächst den Rentenendwert Kn über die Formeln der Kapitalentwicklung mit festem Zinssatz: |
 |
| Den so ermittelten Rentenendwert setzen wir dem Rentenendwert der nachschüssigen Zahlungen gleich. |
 |
| Jetzt dividieren wir noch entsprechend den Regeln der Äquivalenzumformung von Gleichungen noch mit qn und erhalten dadurch die Rentenbarwert |
 |
Der Rentenbarwert mit vorschüssiger Zahlung
| Den vortschüssigen Barwert K0 erhalten wir durch Abzinsung des vorschüssigen Rentenendwertes Kn. Wir berechnen zunächst den Rentenendwert Kn über die Formeln der Kapitalentwicklung mit festem Zinssatz: |
|
| Den so ermittelten Rentenendwert setzen wir dem Rentenendwert der vorschüssigen Zahlungen gleich. |
 |
| Jetzt dividieren wir noch entsprechend den Regeln der Äquivalenzumformung von Gleichungen noch mit qn und erhalten dadurch die Rentenbarwert |
 |
Die ewige Rente
| Unter einer ewigen Rente verstehen wir die jährliche bzw. monatliche Kapitalentnahme von einem bestehenden Guthaben nur in Höhe der Verzinsung des Guthabens. De facto bleibt der anfänglich eingezahlte Grundbetrag unberührt und lediglich die Zinsen werden abgehoben. Die ewige Rente ist defacto der Zinsertrag einer Kapitalanlage, so wie wir sie im Kapitel Zinsrechnung kennen gelernt haben. |
| Titel Aufgabenblatt | Level / Blattnr. |  |
Rentenrechnung mit Zinseszinsen Aufgabenblatt Level 1 / Blatt 1   35 Aufgaben im Blatt |
Rentenrechnung mit Zinseszinsen Aufgabenblatt Level 2 / Blatt 1  24 Aufgaben im Blatt |
- Geschrieben von Dr.-Ing. Meinolf Müller Dr.-Ing. Meinolf Müller
- Zuletzt aktualisiert: 27. Februar 2020 27. Februar 2020
