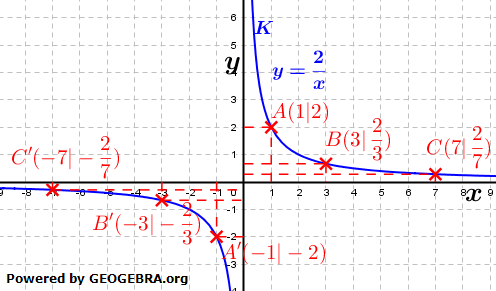
 Gegeben sei die gebrochen-rationale Funktion f mit Gegeben sei die gebrochen-rationale Funktion f mit 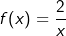 . Die rechte Abbildung zeigt den Graphen von f. Betrachten wir die Punkte A, B und C sowie deren „Spiegelpunkte“ A', B' und C', so stellen wir fest, dass die jeweiligen y-Werte die Spiegel an der x-Achse, die x-Werte die jeweiligen Spiegel an der y-Achse sind. . Die rechte Abbildung zeigt den Graphen von f. Betrachten wir die Punkte A, B und C sowie deren „Spiegelpunkte“ A', B' und C', so stellen wir fest, dass die jeweiligen y-Werte die Spiegel an der x-Achse, die x-Werte die jeweiligen Spiegel an der y-Achse sind.
Wir können hieraus den Merksatz für die Punktsymmetrie herleiten, nämlich |
Merksatz Punktsymmetrie
|
Der Graph einer Funktion f mit der Definitionsmenge 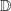 ist genau dann punktsymmetrisch zum Ursprung O(0|0), wenn für alle ist genau dann punktsymmetrisch zum Ursprung O(0|0), wenn für alle 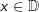 gilt: gilt: |
|
|
-f(-x)=f(x) |
|
|
|
Hinweis:
Im Schulbetrieb wird eigentlich gelehrt, dass f(-x)=-f(x) ist. Die hier aufgeführte Regel mit -f(-x)=f(x) ist identisch, denn die Multiplikation von f(-x)=-f(x) mit -1 führt ja zu -f(-x)=f(x). Letztere Formel führt jedoch zu einfacheren Berechnungen, wenn Symmetrie rechnerisch nachgewiesen werden soll. |




