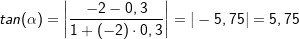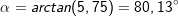|
|
Lineare Funktionen (Geraden) der Funktionsklassen |


Die lineare Funktion (Gerade)
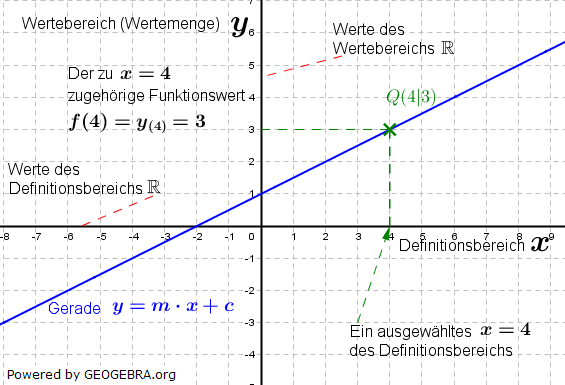 Den angeführten Definitions-begriff einer Funktion verdeutlicht die nebenstehende Graphik. Den angeführten Definitions-begriff einer Funktion verdeutlicht die nebenstehende Graphik.Jedem einzelnen x ist durch die Funktionsvorschrift y=m⋅x+c genau ein und nur ein y-Wert zugeordnet. In der allgemeinen Geraden-gleichung f(x)=y=m⋅x+c haben die Variablen m und c die nachfolgende Bedeutung: m steht für die „Steigung“ der Geraden. c steht für den „y-Achsenabschnitt“ der Geraden. |
Die Steigung m einer linearen Funktion
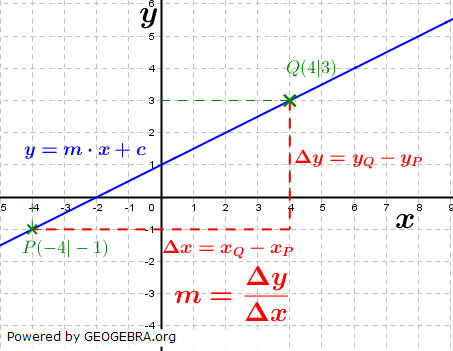 Die Steigung m einer linearen Funktion lässt sich berechnen, wenn die Koordinaten zweier Punkte, durch die die lineare Funktion verläuft, bekannt sind. Die Steigung m einer linearen Funktion lässt sich berechnen, wenn die Koordinaten zweier Punkte, durch die die lineare Funktion verläuft, bekannt sind.Sie wird berechnet über den Differenzenquotienten Δy/Δx. In nebenstehender Graphik sind die beiden Punkte P(-4|-1) und Q(4|3) bekannt. Δy ergibt sich aus yQ-yP=3-(-1)=4. Δx ergibt sich aus xQ-xP=4-(-4)=8. Somit ergibt sich: 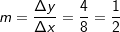 . .Die Funktionsgleichung lautet somit 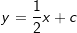 . .Es fehlt noch die Bestimmung von c. |
Der y-Achsenabschnitt c einer linearen Funktion
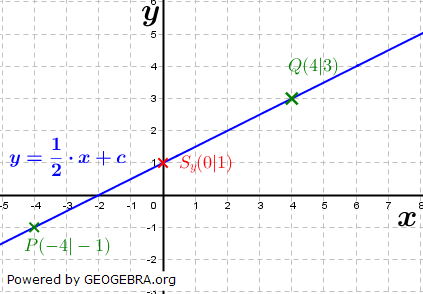 Unter dem y-Achsenabschnitt einer linearen Funktion verstehen wir den Schnittpunkt des Graphen der linearen Funktion mit der y-Achse. In nebenstehender Graphik ist dieser Punkt Sy benannt. Unter dem y-Achsenabschnitt einer linearen Funktion verstehen wir den Schnittpunkt des Graphen der linearen Funktion mit der y-Achse. In nebenstehender Graphik ist dieser Punkt Sy benannt.Der Wert von c kann rechnerisch ermittelt werden, nachdem die Steigung m bekannt ist. Wir machen mit einem der beiden Punkte P bzw. Q eine Punktprobe und errechnen daraus den Wert von c. Welchen Punkt wir dabei auswählen, ist egal. Wir führen die Rechnung mit dem Punkt Q(4|3) durch:
|
||||||||||||
Die Punkt-Steigungsformel einer linearen Funktion
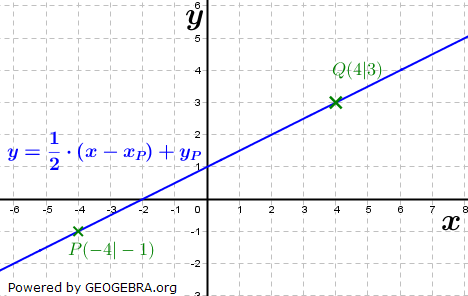 Neben der allgemeinen Funktionsgleichung einer linearen Funktion f(x)=y=m∙x+c existieren noch weitere Gleichungsarten. Eine dieser weiteren Gleichungsarten ist die Punkt-Steigungsformel mit Neben der allgemeinen Funktionsgleichung einer linearen Funktion f(x)=y=m∙x+c existieren noch weitere Gleichungsarten. Eine dieser weiteren Gleichungsarten ist die Punkt-Steigungsformel mitf(x)=y=m∙(x-xP)+yP. Hierin sind xP und yP die Koordinaten eines bekannten Punktes der Geraden. Neben dem bekannten Punkt muss auch noch die Steigung der Geraden bekannt sein, damit die Punkt-Steigungsformel aufgestellt werden kann. Wir stellen die Gleichung auf mit der Steigung 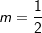 und dem Punkt und dem Punkt 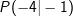 . .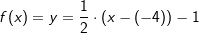 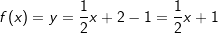 |
Achsenabschnittsform einer linearen Funktionsgleichung
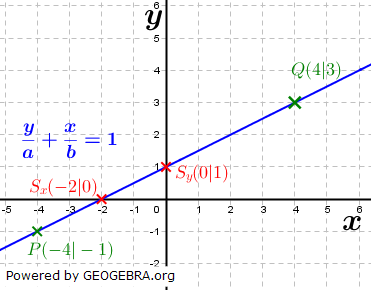 Eine weitere Gleichungsart ist die Achsenabschnittsform mit Eine weitere Gleichungsart ist die Achsenabschnittsform mit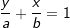 Hierin ist a die y-Koordinate des Schnittpunktes der Geraden mit der y-Achse und b die x-Koordinate des Schnittpunktes der Geraden mit der x-Achse. Wir stellen die Funktions-gleichung auf mit a=1 und b=-2 (Siehe Graphik).
|
|||||||||
Orthogonalität zweier Geraden
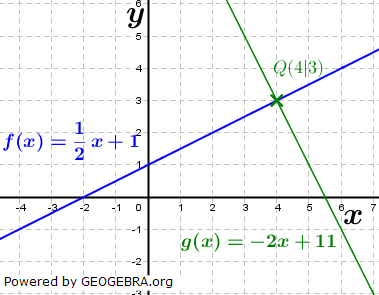 Stehen zwei Geraden f und g senkrecht aufeinander, so gilt die Beziehung Stehen zwei Geraden f und g senkrecht aufeinander, so gilt die Beziehungmf⋅mg=-1. Hierin sind mf und mg die Steigungen der beiden Geraden. Wir stellen die Funktionsgleichung einer Geraden g auf, die orthogonal zur Geraden f mit 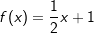 ist und zusätzlich durch den Punkt Q(4|3) geht. ist und zusätzlich durch den Punkt Q(4|3) geht. 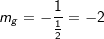
|
|||||||||
Auffrischung Mittelstufenwissen
| Graphen linearer Funktionen haben einen eigenen Namen – Gerade. Die allgemeine Funktionsgleichung lautet: |
| f(x)=m⋅x+c |
Einfluss des Parameters m
Der Parameter 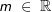 bestimmt die Steigung der Geraden. Es gilt: bestimmt die Steigung der Geraden. Es gilt:
|
Einfluss des Parameters c
Der Parameter 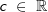 bestimmt den y-Achsenabschnitt. Es gilt: bestimmt den y-Achsenabschnitt. Es gilt:
|
Erweitertes Wissen lineare Funktionen
| Zum erweiterten Wissen zu linearen Funktionen gehören die Themenkreise • Besondere Lage von Geraden; • Länge einer Strecke zwischen zwei Geradenpunkten; • Schnittwinkel einer Geraden mit der x-Achse; • Schnittwinkel zwischen zwei Geraden. Nachfolgend werden die einzelnen Themenkreise behandelt. |
Besondere Lage von Geraden
|
|
Merksatz besondere Lage von Geraden
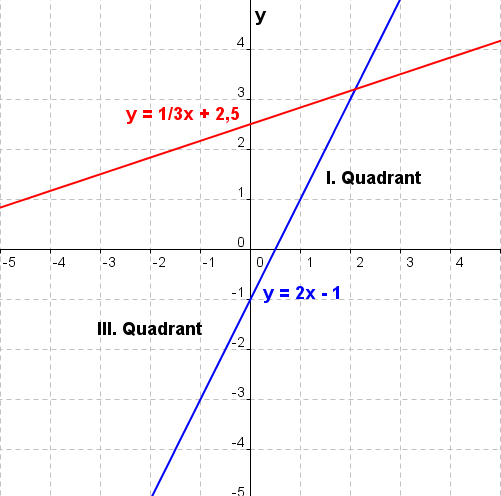
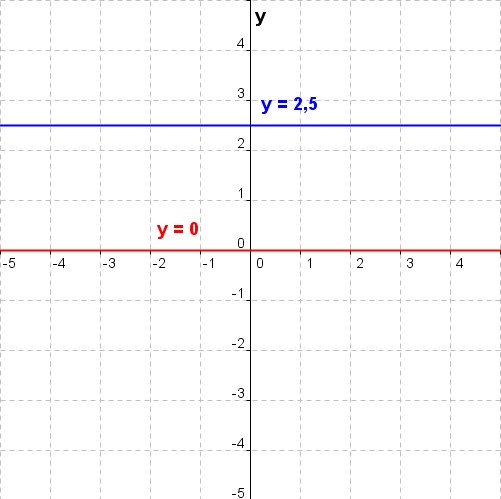
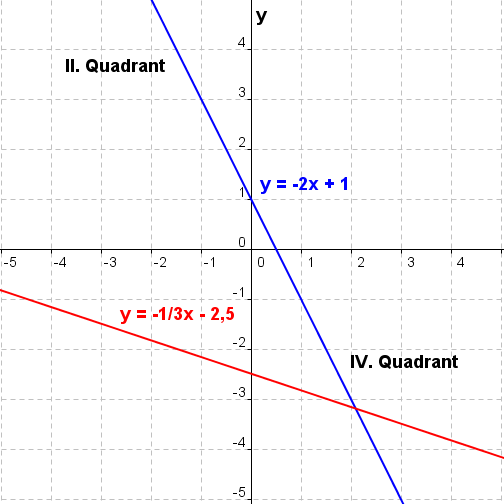
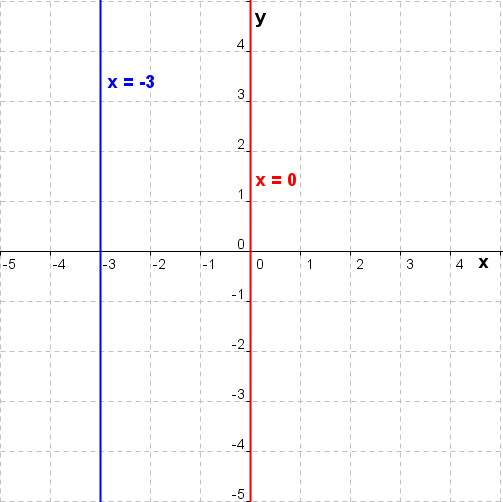
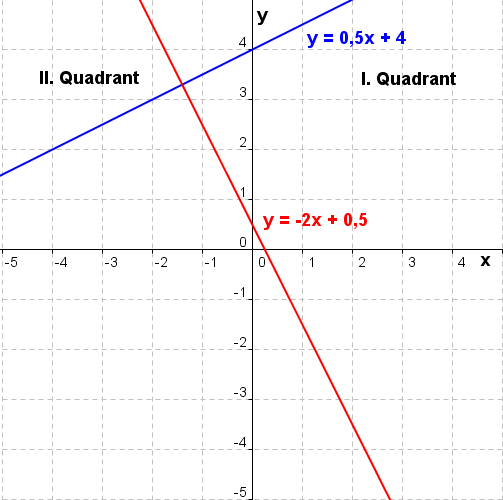
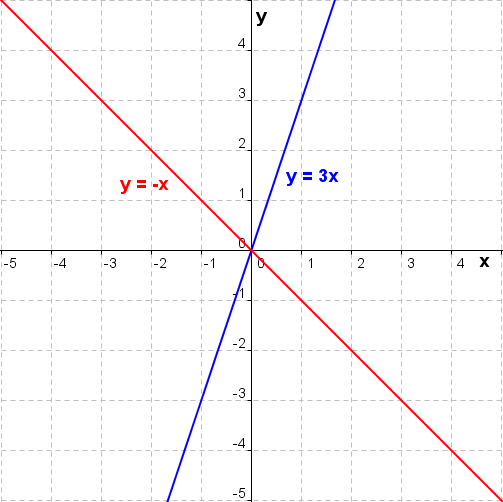
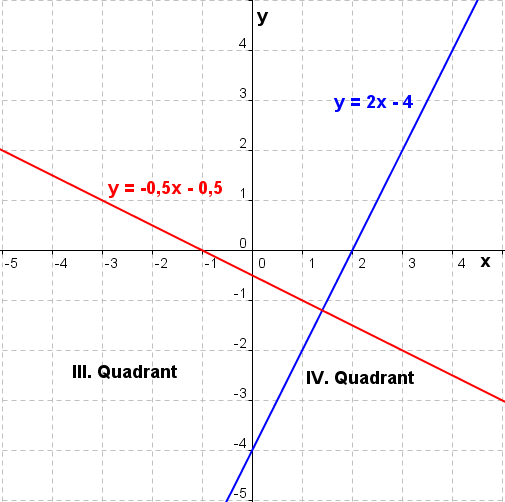
| Haben zwei Geraden g und h die gleiche Steigung m und einen unterschiedlichen y–Achsenabschnitt c, so liegen sie parallel zueinander. Haben zwei Geraden g und h die gleiche Steigung m und denselben y–Achsenabschnitt c, so liegen sie aufeinander. Ist das Produkt der Steigungen zweier Geraden g und h gleich -1, so stehen sie aufeinander senkrecht. (mg∙mh=-1). |
Länge einer Strecke
Merksatz Länge von Strecken
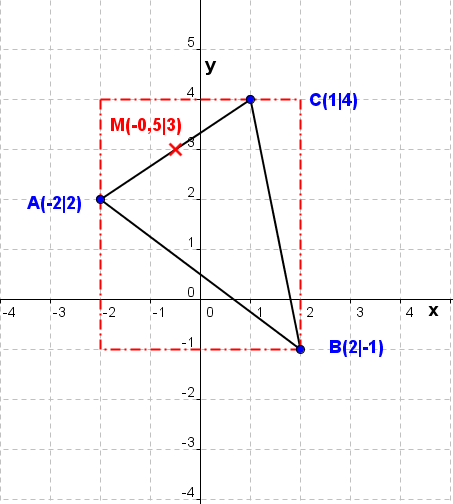
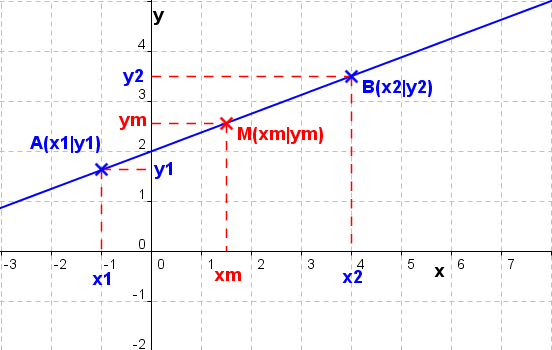 Die Länge einer Strecke Die Länge einer Strecke 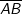 mit A(x1|y1) und B(x2 |y2) errechnet sich über: mit A(x1|y1) und B(x2 |y2) errechnet sich über: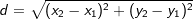 . .Der Mittelpunkt M(xm|ym) einer Strecke 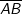 mit A(x1|y1) und B(x2|y2) errechnet sich über: mit A(x1|y1) und B(x2|y2) errechnet sich über: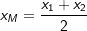 und und 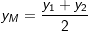 . . |
Schnittwinkel Gerade mit der x-Achse
| Wir unterscheiden zwei Arten von Winkeln bei Geraden, dem Steigungswinkel und dem Schnittwinkel. | ||||
|
||||
Merksatz Schnittwinkel mit der x-Achse
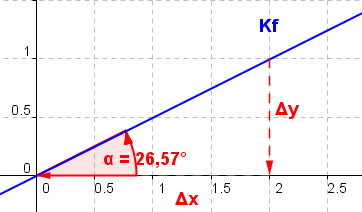 Unter dem Steigungswinkel α einer Geraden g verstehen wir den Winkel zwischen 0° und 180°, den die Gerade g mit der x–Achse gegen den Uhrzeigersinn gesehen bildet. Unter dem Steigungswinkel α einer Geraden g verstehen wir den Winkel zwischen 0° und 180°, den die Gerade g mit der x–Achse gegen den Uhrzeigersinn gesehen bildet.α=∢(x-Achse;g) |
Schnittwinkel zweier Geraden
| Zwei nicht parallele Geraden g und h schneiden sich unter einem Winkel. Als Schnittwinkel ist dabei der spitze Winkel definiert, den die beiden Geraden einschließen. |
Merksatz Schnittwinkel zweier Geraden
Der Schnittwinkel zwischen zwei Geraden g und h ist immer der Winkel, der zwischen 0° und 90° liegt. Die Formel zur Berechnung des Schnittwinkels lautet 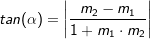 . Dabei ist es unerheblich, welche der beiden Steigungen mit m1 und m2 gewählt wird. Wichtig für die korrekte Berechnung ist das Einhalten der Betragszeichen | |. . Dabei ist es unerheblich, welche der beiden Steigungen mit m1 und m2 gewählt wird. Wichtig für die korrekte Berechnung ist das Einhalten der Betragszeichen | |. |
Lineare Funktionen der Anwendungsorientierung
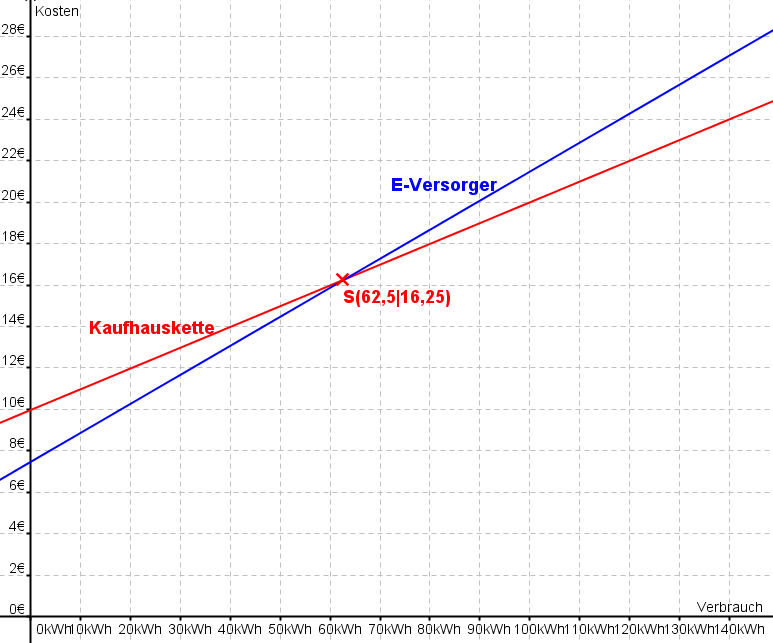
| Viele Themen des Alltags lassen sich über lineare Funktionen mathematisch beschreiben, wie etwa die Strom- und Wasserrechnung eines Energielieferanten, die Handyrechnung des Mobilfunkanbieters, aber auch Angebotskalkulation, Nachfrageermittlung und Marktgleichgewichtsrechnungen. Wir machen uns das an zwei Beispielen klar. | ||||||||||||||||||||
Beispiel 8
|
||||||||||||||||||||
| Titel Aufgabenblatt | Level / Blattnr. |
Lineare Funktionen (Geraden) Aufgabenblatt Level 1 / Blatt 1  16 Aufgaben im Blatt |
Lineare Funktionen (Geraden) Aufgabenblatt Level 1 / Blatt 2  41 Aufgaben im Blatt |
Lineare Funktionen (Geraden) Aufgabenblatt Level 2 / Blatt 1  15 Aufgaben im Blatt |
Lineare Funktionen (Strecken auf Geraden) Aufgabenblatt Level 2 / Blatt 2  24 Aufgaben im Blatt |
Lineare Funktionen Geraden/Schnittwinkel Aufgabenblatt Level 2 / Blatt 3  20 Aufgaben im Blatt |
Lineare Funktionen (Geraden) Aufgabenblatt Level 2 / Blatt 4  13 Aufgaben im Blatt |
Lineare Funktionen (anwendungsorientiert) Aufgabenblatt Level 3 / Blatt 1  14 Aufgaben im Blatt |
Lineare Funktionen (anwendungsorientiert) Aufgabenblatt Level 3 / Blatt 2  20 Aufgaben im Blatt |
Lineare Funktionen mit Parameter Aufgabenblatt Level 3 / Blatt 3  16 Aufgaben im Blatt |
Lineare Funktionen mit Parameter Aufgabenblatt Level 3 / Blatt 4  19 Aufgaben im Blatt |
Lineare Funktionen mit Parameter Aufgabenblatt Level 3 / Blatt 5  11 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021

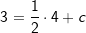
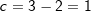
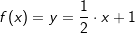
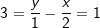
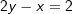
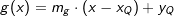
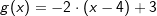
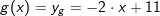
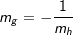 bzw.
bzw. 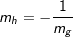 .
.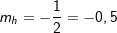 . Die Steigung der Geraden h beträgt -0,5.
. Die Steigung der Geraden h beträgt -0,5.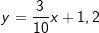 . Mache eine Aussage über die gegenseitige Lage der Geraden g und h.
. Mache eine Aussage über die gegenseitige Lage der Geraden g und h.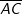 .
.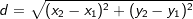 .
.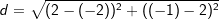
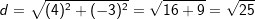
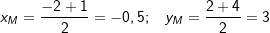
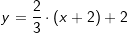
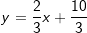 .
.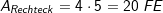
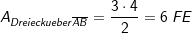
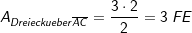
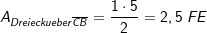
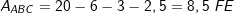
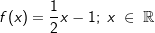 . Unter welchem Winkel schneidet f die x-Achse?
. Unter welchem Winkel schneidet f die x-Achse? folgt für den gesuchten Winkel:
folgt für den gesuchten Winkel:
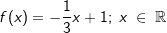 . Unter welchem Winkel schneidet f die x-Achse?
. Unter welchem Winkel schneidet f die x-Achse?
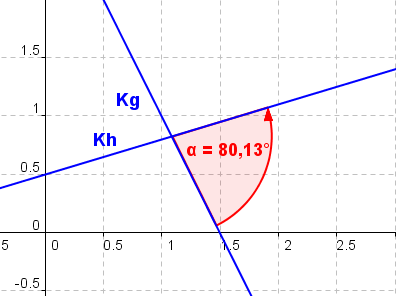 Die Geraden Kg und Kh schließen zwei Winkel ein. Den kleineren der beiden Winkel, der zwischen 0° und 90° liegt, bezeichnen wir mit Schnittwinkel von Kg und Kh.
Die Geraden Kg und Kh schließen zwei Winkel ein. Den kleineren der beiden Winkel, der zwischen 0° und 90° liegt, bezeichnen wir mit Schnittwinkel von Kg und Kh.