 |
Quadratische Funktionen (Parabeln) Level 1 - Grundlagen - Aufgabenblatt 4 |
| Dokument mit 45 Aufgaben |
Aufgabe A1 (4 Teilaufgaben)
Gib die Anzahl der gemeinsamen Punkte der Graphen von f und g an. |
 Eine Frage stellen... |
| Gemeinsame Punkte sind Schnittpunkte bzw. Berührpunkte. Solche Punkte bestimmt man durch Gleichsetzung. Da in dieser Aufgabe nur die Anzahl gemeinsamer Punkte gefragt ist, genügt es, den Wert der Diskriminante der sich ergebenden quadratischen Gleichung zu bestimmen. |
 Fehler melden... |
Aufgabe A2 (4 Teilaufgaben)
Beschreibe die gegenseitige Lage der Graphen von f und g. Gib gegebenenfalls die gemeinsamen Punkte an. |
| Eine Frage stellen... |
| Ein Punkt liegt dann auf der Normalparabel (mit der Funktionsgleichung f(x)=x2), wenn mit einer Punktprobe eine wahre Aussage eintritt. Bei einer Punktprobe musst du den Ausdruck f(x) durch den y-Wert des Punktes ersetzen und den x-Wert in die Funktionsgleichung einsetzen. |
| Fehler melden... |
Aufgabe A3 (3 Teilaufgaben)
Zeige, dass die Gerade zur Funktion f eine Tangente an den Graphen der Funktion ist. Bestimme die Koordinaten des Berührpunktes und zeichne die Graphen. |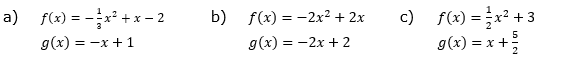
| Eine Frage stellen... |
| Hierzu müssen wir die Funktion f mit der Geraden gleichsetzen und nach x auflösen. Ist die Gerade eine Tangente an f, dann hat die entstehende quadratische Gleichung nur eine Lösung. Abschließend musst du noch die zugehörige y-Koordinate berechnen und dann die Graphen zeichnen. |
| Fehler melden... |
Aufgabe A4 (3 Teilaufgaben)
Ordne den Funktionstermen deren zugehörigen Graphen zu. Lies die Schnittpunkte bzw. den Berührpunkt ab und überprüfe deinen Vorschlag durch Rechnung. |
| Eine Frage stellen... |
Die Darstellung  bedeutet, dass eine Gerade g mit  mit der Funktion f mit  geschnitten wird und daraus die Schnittpunkte der Graphen der beiden Funktionen ermittelt werden können.Entsprechend dieser Darstellung können die Grafiken den Gleichungen zugeordnet werden. |
| Fehler melden... |
Aufgabe A5 (3 Teilaufgaben)
Bestimme den Parameter der Geradengleichung so, dass die Gerade den Graphen von f berührt. Ermittle die Koordinaten des Berührpunktes. |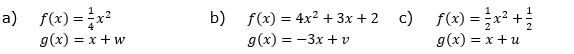
| Eine Frage stellen... |
| Wir müssen die Funktionsgleichungen der Geraden g mit der Funktionsgleichung der Parabel f gleichsetzen und den Funktionsterm nach x auflösen (Mitternachtsformel). In der Diskriminanten der Lösung befindet sich dann der Parameter, der so gesetzt werden muss, dass die Diskriminante den Wert 0 enthält. |
| Fehler melden... |
Aufgabe A6 (4 Teilaufgaben)
Der Graph der linearen Funktion g geht durch P und Q. Gib den Funktionsterm von an g und zeige, dass der Graph von g eine Tangente an den Graphen von f ist. |
| Eine Frage stellen... |
Wir müssen die Funktionsgleichungen der Geraden g durch zwei Punkte aufstellen, indem wir zuerst die Steigung über 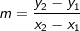 ermitteln und dann mit einer Punktprobe das absolute Glied der Geradengleichung ermitteln.Danach müssen wir die Geradengleichung mit der Funktionsgleichung der Parabel schneiden und nachweisen, dass es nur einen Schnittpunkt gibt, der ja dann ein Berührpunkt sein muss. |
| Fehler melden... |
Aufgabe A7 (5 Teilaufgaben)
| Bestimme die Funktion f, deren Graph K die folgenden Eigenschaften besitzt: | |
| a) | K ist achsensymmetrisch und geht durch P(-1│-2) und Q(2│7). |
| b) | K ist eine verschobene Normalparabel, die durch P(2│-1) und Q(-1│5). |
| c) | K geht durch den Ursprung, schneidet die x-Achse bei N(2│0) und verläuft durch P(-1│-1,5). |
| d) | K ist eine an der x-Achse gespiegelte, verschobene Normalparabel, die durch P(1│6) und Q(4│3) verläuft. |
| e) | K verläuft durch die Punkte P(0│2),Q(-1|-3) und R(1│1). |
| Eine Frage stellen... |
Aufgabe A8 (4 Teilaufgaben)
Der Graph einer quadratischen Funktion f geht durch den Punkt Q und schneidet die x-Achse in N1 und N2. Bestimme den Funktionsterm von f und gib diesen in der Hauptform an. |
| Eine Frage stellen... |
| Gegeben sind zwei Nullstellen und ein weiterer Punkt. Wir stellen die Faktorengleichung (Nullstellengleichung) f(x)=a∙(x-x1)∙(x-x2) der Parabel auf und machen mit dem gegebenen Punkt eine Punktprobe zur Ermittlung von a. |
| Fehler melden... |
Aufgabe A9 (3 Teilaufgaben)
Der Graph einer quadratischen Funktion f hat den Scheitel S und geht durch den Punkt P. Bestimme ihren Funktionsterm. |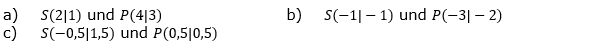
| Eine Frage stellen... |
| Gegeben ist der Scheitel und ein weiterer Punkt. Wir stellen die Scheitelform f(x)=a∙(x-xS )^2+yS der Parabel auf und machen mit dem gegebenen Punkt eine Punktprobe zur Ermittlung von a. |
| Fehler melden... |
Aufgabe A10 (3 Teilaufgaben)
| Der Graph einer quadratischen Funktion f geht durch die folgenden Punkte. Bestimme mit einem passenden Ansatz einen Funktionsterm. | |
| a) | Scheitel S(-6|3) und Punkt  |
| b) | Achsenschnittpunkte N1(-2│0), N2(6|0) und R(0|-1,2) |
| Eine Frage stellen... |
Aufgabe A11
| Eine quadratische Funktion f hat bei x1=-3 und x2=-1 Nullstellen. Der größte Funktionswert beträgt 1. Bestimme den Funktionsterm. |
| Eine Frage stellen... |
| Gegeben sind zwei Nullstellen und ein maximaler Funktionswert (y-Wert) 1. Wir müssen hierzu zunächst noch den x-Wert des maximalen Funktionswertes bestimmen. Aus Symmetriegründen liegt dieser x-Wert in der Mitte der beiden Nullstellen. Damit ist der Scheitel bekannt. |
| Fehler melden... |
Aufgabe A12
| Der Graph einer quadratischen Funktion f ist symmetrisch zur y-Achse und geht durch die Punkte P(0│5) und Q(1│3). Bestimme den Funktionsterm. |
| Eine Frage stellen... |
| Eine achsensymmetrische Parabel ist in x-Richtung unverschoben, hat somit die Funktionsgleichung f(x)=ax2+c. Wir machen mit den gegebenen Punkten eine Punktprobe und lösen das Gleichungssystem nach a und c auf. |
| Fehler melden... |
Aufgabe A13 (2 Teilaufgaben)
| a) | Stelle fest, welche der folgenden Punkte auf der um 2 Einheiten nach rechts und im 1,4 Einheiten nach unten verschobenen Parabel liegen. | |||||
| (I) | P1(1|19,6) | (II) | P2(4|2,6) | (II) | P3(-2|4,6) | |
| (IV) | P4(-3|23,6) | (V) | P5(-1|7,6) | |||
| b) | An welchen Stellen nimmt die Funktion den Wert (1) 7,6; den Wert; (2) 2,6 an? | |||||
| Eine Frage stellen... |
Aufgabe A14 (5 Teilaufgaben)
| Zeichne die Normalparabel mit den angegebenen Eigenschaften. Notiere den Term der dazugehörigen Funktion. | |
| a) | S(-2|-1) ist der Scheitelpunkt. |
| b) | An den Stellen -2 und 4 wird die x-Achse von der Parabel geschnitten. |
| c) | Die Parabel geht durch den Ursprung und hat die Gerade x=2 als Symmetrieachse. |
| d) | Der Scheitelpunkt hat -3 als y-Koordinate. Der Ursprung ist Punkt der Parabel. |
| e) | Die Parabel geht durch die Punkte P1 (-1|7) und P2 (3|7). |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Quadratische Funktionen (Parabeln) Level 1 - Grundlagen - Aufgabenblatt 4 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
