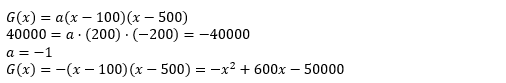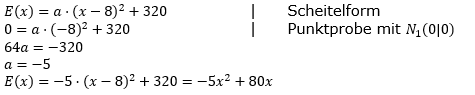 |
Quadratische Funktionen (anwendungsorientiert) Level 3 - Expert - Aufgabenblatt 1 |
| Dokument mit 14 Aufgaben |
In diesem Aufgabenblatt befinden sich Aufgaben zu anwendungsorientierten Themen.
Aufgabe A1
| Eine Flüssigkeit wird auf 90 °C erhitzt. Dann lässt man sie bei einer Umgebungstemperatur von 20 °C abkühlen. Bei diesem Experiment erhält man folgende Messreihe. | |||||||||
| Zeit t in Minuten | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Temperatur in °C | 90 | 58 | 40 | 31 | 26 | 22 | 22 | 21 | |
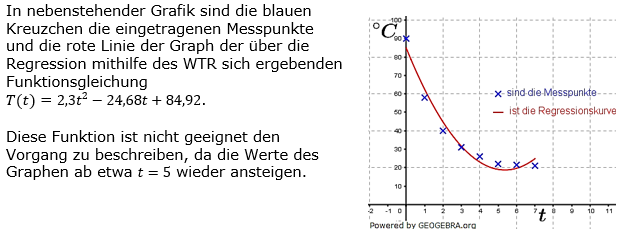
| Stelle die Messdaten in einem Koordinatensystem dar. Bestimme eine Gleichung einer Regressionskurve und zeichne die Kurve in das Koordinatensystem ein. Beurteile die Regressionskurve. |
|||||||||
 Eine Frage stellen... |
 Die Vorgehensweise zur Erstellung einer Regression kannst du im → „WIKI quadratische Funktionen“ nachlesen. |
 Fehler melden... |
Aufgabe A2 (4 Teilaufgaben)
| Über die Gesamtkosten eines Betriebes in € ist Folgendes bekannt: Für eine Produktion von 10 Stück entstehen Gesamtkosten von 1050 €, bei 20 Stück sind es 1400 €. |
|
| a) | Bestimme die Kostenfunktion K unter der Annahme, dass es sich um eine quadratische Funktion handelt und die Fixkosten 900 € betragen. |
| b) | Für welche Produktionsmenge entstehen Gesamtkosten von 1200 €? |
| c) | Bestimme die Gewinnzone und den größten Gewinn, wenn die produzierte Menge zum Stückpreis von 85 € verkauft wird. |
| d) | Wie groß ist der mittlere Kostenzuwachs im Intervall [10;30]? |
| Eine Frage stellen... |
| Aus dem Text der Aufgabenstellung heraus müssen wir die Bedingungen für das Aufstellen der Kostenfunktion als quadratische Funktion feststellen. Dies sind vor allem: Die Parabel verläuft durch den Punkt Sy (0|900) (resultierend aus den Fixkosten) Die Parabel verläuft durch den Punkt P(10|1050) (Gesamtkosten für 10 ME) Die Parabel verläuft durch den Punkt P(20|1400) (Gesamtkosten für 20 ME) |
Aufgabe A3
 Der parabelförmige Brückenbogen einer Brücke hat eine Spannweite von 170 Metern. Im Abstand von 2,5 Meter zum Fußpunkt der Brücke ist der Brückenbogen 6,28 Meter hoch. Wie hoch ist der Brückenbogen? |
| Eine Frage stellen... |
| Aus dem Text der Aufgabenstellung heraus müssen wir die Bedingungen für das Aufstellen der Parabelfunktion des Brückenbogens feststellen. Dabei müssen wir zunächst die Lage des Koordinatensystems bestimmen. Wir wählen die y-Achse als Symmetrieachse, sodass wir wegen der Gesamtbreite von zwei Nullstellen erhalten, nämlich N1(-85|0) und N2(85|0). Im Abstand von 2,5 m zur Nullstelle ist der Brückenbogen 6,28 m hoch. Dies führt uns zu einem weiteren Punkt, nämlich P(82,5|6,28). Aufstellung der Funktionsgleichung des Parabelbogens über zwei Nullstellen und einen weiteren Punkt. |
Aufgabe A4 (2 Teilaufgaben)
| Das rechteckige Spielfeld beim American Football hat eine Fläche von höchstens 10800 m2. Die Breite ist 30 m kürzer als die Länge. | |
| a) | Zeige, dass die Länge folgende Ungleichung erfüllt: x2-30x-10800 ≤ 0 |
| b) | Welche Breite darf das Fußballfeld haben, wenn es mindestens 90 m lang sein muss? |
| Eine Frage stellen... |
Aufgabe A5
Die Fixkosten für die Produktion einer Ware belaufen sich auf 330 Geldeinheiten (GE). Werden 10 Mengeneinheiten (ME) der Ware hergestellt, erhöhen sich die Gesamtkosten um 30 GE. Bei 20 ME betragen die Gesamtkosten 410 GE. Prüfe, ob die Gesamtkosten durch die Kostenfunktion K mit 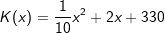 richtig beschrieben werden. Wie hoch muss der Preis pro ME festgelegt werden, damit die Nutzenschwelle bei 30 ME liegt? In welchem Bereich wird dann mit Gewinn produziert? |
| Eine Frage stellen... |
Aufgabe A6
| Der Gewinn in € wird durch eine ganzrationale Funktion zweiten Grades in Abhängigkeit von der nachgefragten Menge beschrieben. Bei 100 ME ist der Gewinn null. Bei 300 ME ist der Gewinn maximal und beträgt dann 40000 €. Bestimme den Funktionsterm für die Gewinnfunktion. |
| Eine Frage stellen... |
| Aus dem Text der Aufgabenstellung heraus müssen wir die Bedingungen für das Aufstellen der Parabelfunktion der Gewinnfunktion feststellen. Wir stellen fest, dass maximaler Gewinn bei 300 ME mit 40000 € Gewinn ist, also ist der Scheitel S(300|40000). Des Weiteren haben wir die Gewinnschwelle (=Nullstelle der Funktionsgleichung) mit N1(100|0) und damit wegen der Symmetrieachse bei x=300 die zweite Nullstelle mit N2(500|0). |
Aufgabe A7
| Ein Unternehmen bietet als Monopolist am Markt eine Ware an. Dadurch hängt der Preis (in €) von der nachgefragten Stückzahl ab. Die Erlöskurve ist eine Parabel, welche die x–Achse in x=16 schneidet. Der größtmögliche Erlös beträgt 320 €. Bestimme die Erlösfunktion. |
| Eine Frage stellen... |
| Aus dem Text der Aufgabenstellung heraus müssen wir die Bedingungen für das Aufstellen der Parabelfunktion der Erlösfunktion feststellen. Es ist einleuchtend, dass bei null Verkäufen der Erlös ebenfalls null ist, also haben wir eine Nullstelle N1(0|0). Weiterhin ist die zweite Nullstelle gegeben mit N2(16|0). Der Größte Erlös liegt im Scheitel mit 320 €. Die Symmetrieachse liegt bei x=8 und damit der Scheitel bei S(8|320). |
Aufgabe A8
| Auf einer Teststrecke wird gemessen, wie viel Benzin ein PKW bei gleichbleibender Geschwindigkeit verbraucht. Dabei hängt der Benzinverbrauch b (in Liter pro 100 km) quadratisch von der Geschwindigkeit v (in km/h) ab: | ||||
| Mit welchem Verbrauch ist durchschnittlich bei 120 km/h zu rechnen? | v | 30 | 40 | 80 |
| b | 6,25 | 6,2 | 7,0 | |
| Eine Frage stellen... |
| Zur Aufstellung der Parabelfunktion des Benzinverbrauchs haben wir drei Punkte gegeben (siehe Tabelle). Wir bilden über diese drei Punkte eine quadratische Regression. |
 Zur Vorgehensweise für die Erstellung einer Regression siehe → „WIKI quadratische Funktionen“.  |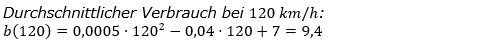
| Fehler melden... |
Aufgabe A9
| Ein Zehnkämpfer stößt einer Kugel so, dass die Flugbahn durch folgenden Funktionsterm beschrieben werden kann: f(x)=-0,0135x²+0,142x+2; x > 0. Die Entfernung vom Wurfkreis wird durch x in Meter gemessen, die Funktionswerte geben die Höhe der Kugel an. Berechne die Nullstelle von f. Welche Bedeutung hat diese Nullstelle? Welche größte Höhe erreicht die Kugel? |
| Eine Frage stellen... |
Aufgabe A10
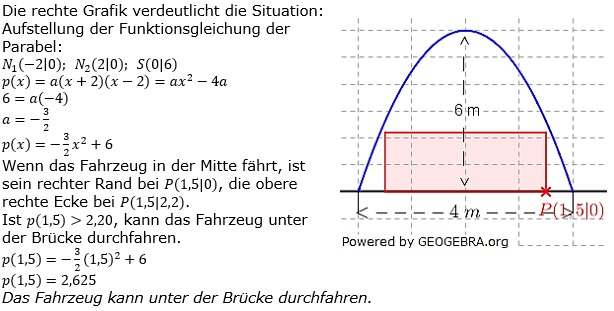
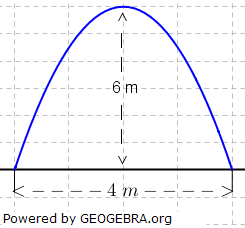 Eine Brückendurchfahrt hat die Form einer Parabel 2. Ordnung. Sie ist 6 m hoch und 4 m breit. Ein Fahrzeug ist 3 m breit und 2,20 m hoch.Kann dieses Fahrzeug noch unter der Brücke durchfahren? |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Quadratische Funktionen (anwendungsorientiert) Level 3 - Expert - Aufgabenblatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
